A Simple Scaling Analysis of Rainfall in Andalusia (Spain) under Different Precipitation Regimes
Abstract
:1. Introduction
2. Materials and Methods
3. Results and Discussion
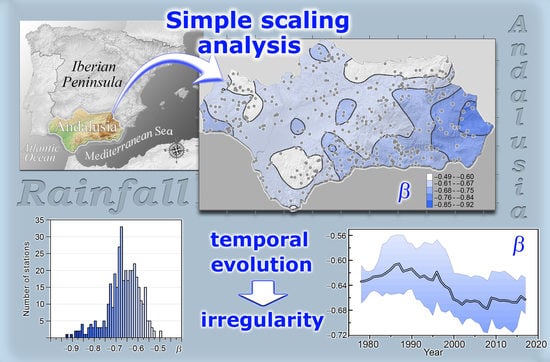
3.1. Spatial Distribution of the Scaling Parameter
3.2. Generalized IDF Equations for the Provincial Capitals of Andalusia
3.3. Climate Trends of the Scaling Parameter β
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Walther, G.R.; Post, E.; Convey, P.; Menzel, A.; Parmesan, C.; Beebee, T.J.; Bairlein, F. Ecological responses to recent climate change. Nature 2002, 416, 389–395. [Google Scholar] [CrossRef] [PubMed]
- Yu, Z.G.; Leung, Y.; Chen, Y.D.; Zhang, Q.; Anh, V.; Zhou, Y. Multifractal analyses of daily rainfall time series in Pearl River basin of China. Phys. A Stat. Mech. Appl. 2014, 405, 193–202. [Google Scholar] [CrossRef] [Green Version]
- García-Marín, A.P.; Jiménez-Hornero, F.J.; Ayuso, J.L. Applying multifractality and the self-organized criticality theory to describe the temporal rainfall regimes in Andalusia (southern Spain). Hydrol. Process. 2008, 22, 295–308. [Google Scholar] [CrossRef]
- Mandelbrot, B.B. The Fractal Geometry of Nature; W.H.Freeman & Co Ltd.: New York, NY, USA, 1982. [Google Scholar]
- Gires, A.; Tchiguirinskaia, I.; Schertzer, D.; Lovejoy, S. Development and analysis of a simple model to represent the zero rainfall in a universal multifractal framework. Nonlin. Process. Geophys. 2013, 20, 343–356. [Google Scholar] [CrossRef] [Green Version]
- García-Marín, A.P.; Ayuso-Muñoz, J.L.; Jiménez-Hornero, F.J.; Estévez, J. Selecting the best IDF model by using the multifractal approach. Hydrol. Process. 2013, 27, 433–443. [Google Scholar] [CrossRef]
- García-Marín, A.P.; Estévez, J.; Medina-Cobo, M.T.; Ayuso-Muñoz, J.L. Delimiting homogeneous regions using the multifractal properties of validated rainfall data series. J. Hydrol. 2015, 529, 106–119. [Google Scholar] [CrossRef]
- Rodríguez, R.; Casas, M.C.; Redaño, Á. Multifractal analysis of the rainfall time distribution on the metropolitan area of Barcelona (Spain). Meteorol. Atmos. Phys. 2013, 121, 181–187. [Google Scholar] [CrossRef] [Green Version]
- Gupta, V.K.; Waymire, E. Multiscaling properties of spatial rainfall and river flow distributions. J. Geophys. Res. Atmos. 1990, 95, 1999–2009. [Google Scholar] [CrossRef]
- Koutsoyiannis, D.; Foufoula-Georgiou, E. A scaling model of storm hyetograph. Water Resour. Res. 1993, 29, 2345–2361. [Google Scholar] [CrossRef]
- Burlando, P.; Rosso, R. Scaling and multiscaling models of depth-duration-frequency curves for storm precipitation. J. Hydrol. 1996, 187, 45–64. [Google Scholar] [CrossRef]
- Menabde, M.; Seed, A.; Pegram, G. A simple scaling model for extreme rainfall. Water Resour. Res. 1999, 35, 335–339. [Google Scholar] [CrossRef]
- Yu, P.S.; Yang, T.C.; Lin, C.S. Regional rainfall intensity formulas based on scaling property of rainfall. J. Hydrol. 2004, 295, 108–123. [Google Scholar] [CrossRef]
- Panthou, G.; Vischel, T.; Lebel, T.; Quantin, G.; Molinié, G. Characterising the space–time structure of rainfall in the Sahel with a view to estimating IDAF curves. Hydrol. Earth Syst. Sci. 2014, 18, 5093–5107. [Google Scholar] [CrossRef] [Green Version]
- Rodríguez-Solà, R.; Casas-Castillo, M.C.; Navarro, X.; Redaño, Á. A study of the scaling properties of rainfall in Spain and its appropriateness to generate intensity-duration-frequency curves from daily records. Int. J. Climatol. 2017, 37, 770–780. [Google Scholar] [CrossRef]
- Innocenti, S.; Mailhot, A.; Frigon, A. Simple scaling of extreme precipitation in North America. Hydrol. Earth Syst. Sci. 2017, 21, 5823–5846. [Google Scholar] [CrossRef] [Green Version]
- Casas-Castillo, M.C.; Llabrés-Brustenga, A.; Rius, A.; Rodríguez-Solà, R.; Navarro, X. A single scaling parameter as a first approximation to describe the rainfall pattern of a place: Application on Catalonia. Acta Geophys. 2018, 66, 415–424. [Google Scholar] [CrossRef]
- Bara, M.; Kohnová, S.; Gaál, L.; Szolgay, J.; Hlavčová, K. Estimation of IDF curves of extreme rainfall by simple scaling in Slovakia. Contrib. Geophys. Geod. 2009, 39, 187–206. [Google Scholar]
- Rodríguez, R.; Navarro, X.; Casas, M.C.; Ribalaygua, J.; Russo, B.; Pouget, L.; Redaño, Á. Influence of climate change on IDF curves for the metropolitan area of Barcelona (Spain). Int. J. Climatol. 2014, 34, 643–654. [Google Scholar] [CrossRef] [Green Version]
- Loaiciga, H.A.; Valdés, J.B.; Vogel, R.; Garvey, J.; Schwarz, H. Global warming and the hydrologic cycle. J. Hydrol. 1996, 174, 83–127. [Google Scholar] [CrossRef]
- Huntington, T.G. Evidence for intensification of the global water cycle: Review and synthesis. J. Hydrol. 2006, 319, 83–95. [Google Scholar] [CrossRef]
- Field, C.B.; Barros, V.; Stocker, T.F.; Qin, D.; Dokken, D.J.; Ebi, K.L.; Mastrandrea, M.D.; Mach, K.J.; Plattner, G.-K.; Allen, S.K.; et al. (Eds.) IPCC 2012—Managing the Risks of Extreme Events and Disasters to Advance Climate Change Adaptation; Cambridge University Press: Cambridge, UK, 2012; 582p. [Google Scholar]
- Christensen, J.H.; Christensen, O.B. Severe summertime flooding in Europe. Nature 2003, 421, 805–806. [Google Scholar] [CrossRef] [PubMed]
- Pérez, F.F.; Boscolo, R. (Eds.) Clima en España: Pasado, Presente y Futuro. Informe de Evaluación del Cambio Climático Regional; CLIVAR; Ministerio de Medio Ambiente y Medio Rural y Marino; Ministerio de Ciencia e Innovacion (MICINN), Spain: 2010; 83p; Available online: http://hdl.handle.net/10261/23600 (accessed on 15 April 2021).
- Lana, X.; Casas-Castillo, M.C.; Rodríguez-Solà, R.; Serra, C.; Martínez, M.D.; Kirchner, R. Rainfall regime trends at annual and monthly scales in Catalonia (NE Spain) and the possible effects of the increasing CO2 emissions into the atmosphere. Theor. Appl. Climatol. 2021, 146, 981–996. [Google Scholar] [CrossRef]
- Herrera-Grimaldi, P.; García-Marín, A.P.; Ayuso-Muñoz, J.L.; Flammini, A.; Morbidelli, R.; Ayuso-Ruíz, A.L. Detection of trends and break points in temperature: The case of Umbria (Italy) and Guadalquivir Valley (Spain). Acta Geophys. 2018, 66, 329–343. [Google Scholar] [CrossRef]
- Llabrés-Brustenga, A.; Rius, A.; Rodríguez-Solà, R.; Casas-Castillo, M.C.; Redaño, Á. Quality control process of the daily rainfall series available in Catalonia from 1855 to the present. Theor. Appl. Climatol. 2019, 137, 2715–2729. [Google Scholar] [CrossRef]
- Hershfield, D.M. Rainfall Frequency Atlas of the United States for Durations from 30 Minutes to 24 Hours and Return Periods from 1 to 100 Years; Weather Bureau Technical Paper 40; U.S. Weather Bureau: Washington, DC, USA, 1961; 115p. Available online: www.weather.gov/media/owp/oh/hdsc/docs/TechnicalPaper_No40.pdf (accessed on 15 April 2021).
- Weiss, L.L. Ratio of true to fixed-interval maximum rainfall. J. Hydraul. Div. 1964, 90, 77–82. [Google Scholar] [CrossRef]
- Papalexiou, S.M.; Dialynas, Y.G.; Grimaldi, S. Hershfield factor revisited: Correcting annual maximum precipitation. J. Hydrol. 2016, 542, 884–895. [Google Scholar] [CrossRef]
- Morbidelli, R.; Saltalippi, C.; Flammini, A.; Cifrodelli, M.; Picciafuoco, T.; Corradini, C.; Casas-Castillo, M.C.; Fowler, J.H.; Wilkinson, S.M. Effect of temporal aggregation on the estimate of annual maximum rainfall depths for the design of hydraulic infrastructure systems. J. Hydrol. 2017, 554, 710–720. [Google Scholar] [CrossRef] [Green Version]
- Morbidelli, R.; Saltalippi, C.; Flammini, A.; Picciafuoco, T.; Dari, J.; Corradini, C. Characteristics of the underestimation error of annual maximum rainfall depth due to coarse temporal aggregation. Atmosphere 2018, 9, 303. [Google Scholar] [CrossRef] [Green Version]
- Llabrés-Brustenga, A.; Rius, A.; Rodríguez-Solà, R.; Casas-Castillo, M.C. Influence of regional and seasonal rainfall patterns on the ratio between fixed and unrestricted measured intervals of rainfall amounts. Theor. Appl. Climatol. 2020, 140, 389–399. [Google Scholar] [CrossRef]
- Jiménez-Hornero, F.J.; García-Marín, A.P.; Ayuso, J.L. Description of the Daily Number of Rain-Free Hours Series from a Location in Southern Spain by Using the Multifractal Turbulence Formalism. J. Hydrol. Eng. 2008, 13, 987–991. [Google Scholar] [CrossRef]
- Martín-Vide, J. Spatial distribution of a daily precipitation concentration index in peninsular Spain. Int. J. Climatol. 2004, 24, 959–971. [Google Scholar] [CrossRef]
- Pérez-Zanón, N.; Casas-Castillo, M.C.; Rodríguez-Solà, R.; Peña, J.C.; Rius, A.; Solé, J.G.; Redaño, À. Analysis of extreme rainfall in the Ebre Observatory (Spain). Theor. App. Climatol. 2015, 124, 935–944. [Google Scholar] [CrossRef] [Green Version]
- Casas-Castillo, M.C.; Rodríguez-Solà, R.; Navarro, X.; Russo, B.; Lastra, A.; González, P.; Redaño, À. On the consideration of scaling properties of extreme rainfall in Madrid (Spain) for developing a generalized intensity-duration-frequency equation and assessing probable maximum precipitation estimates. Theor. Appl Climatol. 2018, 131, 573–580. [Google Scholar] [CrossRef]












Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Casas-Castillo, M.d.C.; Rodríguez-Solà, R.; Llabrés-Brustenga, A.; García-Marín, A.P.; Estévez, J.; Navarro, X. A Simple Scaling Analysis of Rainfall in Andalusia (Spain) under Different Precipitation Regimes. Water 2022, 14, 1303. https://doi.org/10.3390/w14081303
Casas-Castillo MdC, Rodríguez-Solà R, Llabrés-Brustenga A, García-Marín AP, Estévez J, Navarro X. A Simple Scaling Analysis of Rainfall in Andalusia (Spain) under Different Precipitation Regimes. Water. 2022; 14(8):1303. https://doi.org/10.3390/w14081303
Chicago/Turabian StyleCasas-Castillo, María del Carmen, Raül Rodríguez-Solà, Alba Llabrés-Brustenga, Amanda Penélope García-Marín, Javier Estévez, and Xavier Navarro. 2022. "A Simple Scaling Analysis of Rainfall in Andalusia (Spain) under Different Precipitation Regimes" Water 14, no. 8: 1303. https://doi.org/10.3390/w14081303
APA StyleCasas-Castillo, M. d. C., Rodríguez-Solà, R., Llabrés-Brustenga, A., García-Marín, A. P., Estévez, J., & Navarro, X. (2022). A Simple Scaling Analysis of Rainfall in Andalusia (Spain) under Different Precipitation Regimes. Water, 14(8), 1303. https://doi.org/10.3390/w14081303