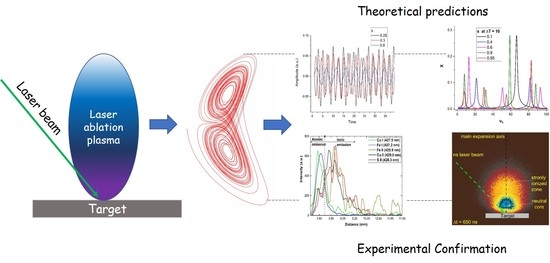
Lorenz Type Behaviors in the Dynamics of Laser Produced Plasma
Abstract
:1. Introduction
2. Mathematical Model
2.1. Route to Non-Differentiability
- (i)
- Any variable used to describe the dynamics of a nondifferential Lorenz type system will be described through multifractal mathematical functions dependent on both the spatial and temporal coordinates, and on the scale resolution.
- (ii)
- The laws describing these dynamics are invariant with respect to the spatial coordinates and temporal transformation, and the scale resolution transformation.
- (iii)
- The constraints on the Lorenz type system dynamics, described through continuous and differentiable curves of a Euclidian space, are replaced by the dynamics of a system lacking any constraints, and being described by continuous and nondifferentiable curves in a multifractal space.
- (iv)
- Between any two points in the multifractal space there is an infinity of curves describing the dynamics of a systems (its geodesics). The indiscernibility between these curves is a natural property of multifractalization through stochasticization; meanwhile, their discernibility is the result of a selection process based on the principle of maximum informational energy [14]. From such a perspective, any Lorenz type system with dynamics described by continuous and differentiable curves has hidden dissipative information (lacks memory). Otherwise, Lorenz type systems described by continuous and nondifferentiable curves have explicit information (presents memory).
Scale Resolutions
2.2. Non-Differentiable Lorenz Type Systems
2.3. Motion Integration
3. Plasma Modelling
4. Experimental Confirmation
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Phipps, C.R. Laser Ablation and Its Applications; Springer Series in Optical Sciences; Springer: Boston, MA, USA, 2007; Volume 129, ISBN 978-0-387-30452-6. [Google Scholar]
- Autrique, D.; Clair, G.; L’Hermite, D.; Alexiades, V.; Bogaerts, A.; Rethfeld, B. The role of mass removal mechanisms in the onset of ns-laser induced plasma formation. J. Appl. Phys. 2013, 114, 023301. [Google Scholar] [CrossRef] [Green Version]
- Toftmann, B.; Schou, J. Time-resolved and integrated angular distributions of plume ions from silver at low and medium laser fluence. Appl. Phys. A Mater. Sci. Process. 2013, 112, 197–202. [Google Scholar] [CrossRef]
- Geohegan, D.B.; Puretzeky, A.A.; Duscher, G.; Pennycook, S.J. Time-resolved imaging of gas phase nanoparticle synthesis by laser ablation. Appl. Phys. Lett. 1998, 72, 2987. [Google Scholar] [CrossRef]
- Irimiciuc, S.A.; Mihaila, I.; Agop, M. Experimental and theoretical aspects of a laser produced plasma. Phys. Plasmas 2014, 21, 093509. [Google Scholar] [CrossRef]
- Irimiciuc, S.A.; Bulai, G.; Gurlui, S.; Agop, M. On the separation of particle flow during pulse laser deposition of heterogeneous materials—A multi-fractal approach. Powder Technol. 2018, 339, 273–280. [Google Scholar] [CrossRef]
- Anisimov, S.I.; Luk’yanchuk, B.S. Selected problems of laser ablation theory. Phys.-Uspekhi 2002, 45, 293–324. [Google Scholar] [CrossRef] [Green Version]
- Bulgakova, N.M.; Stoian, R.; Rosenfeld, A.; Hertel, I.V.; Marine, W.; Campbell, E.E.B. A general continuum approach to describe fast electronic transport in pulsed laser irradiated materials: The problem of Coulomb explosion. Appl. Phys. A Mater. Sci. Process. 2005, 81, 345–356. [Google Scholar] [CrossRef]
- Kelly, R.; Miotello, A. On the role of thermal processes in sputtering and composition changes due to ions or laser pulses. Nucl. Instrum. Methods Phys. B 1998, 141, 49–60. [Google Scholar] [CrossRef]
- Bulgakova, N.M.; Stoian, R.; Rosenfeld, A.; Hertel, I.V. Continuum Models of Ultrashort Pulsed Laser Ablation. In Laser-Surface Interactions for New Materials Production; Miotello, A., Ossi, P., Eds.; Springer: Berlin/Heidelberg, Germany, 2010; Volume 130, pp. 81–97. [Google Scholar]
- Autrique, D.; Chen, Z.; Alexiades, V.; Bogaerts, A.; Rethfeld, B. A multiphase model for pulsed ns-laser ablation of copper in an ambient gas. AIP Conf. Proc. 2012, 1464, 648–659. [Google Scholar] [Green Version]
- Irimiciuc, S.; Bulai, G.; Agop, M.; Gurlui, S. Influence of laser-produced plasma parameters on the deposition process: In situ space- and time-resolved optical emission spectroscopy and fractal modeling approach. Appl. Phys. A Mater. Sci. Process. 2018, 615, 1–14. [Google Scholar] [CrossRef]
- Irimiciuc, S.A.; Gurlui, S.; Nica, P.; Focsa, C.; Agop, M. A compact non-differential approach for modeling laser ablation plasma dynamics. J. Appl. Phys. 2017, 121, 083301. [Google Scholar] [CrossRef]
- Merches, I.; Agop, M. Differentiability and Fractality in Dynamics of Physical Systems; World Scientific: Singapore, 2015; ISBN 978-981-4678-38-4. [Google Scholar]
- Haken, H. Synergetics; Springer: Berlin, Germany, 1983; ISBN 978-3-642-88338-5. [Google Scholar]
- Arfken, G.; Weber, H.; Harris, F.E. Mathematical Methods for Physicsists, 7th ed.; Academic Press: Cambridge, MA, USA, 2012; ISBN 9780123846556. [Google Scholar]
- Dachraoui, H.; Husinsky, W.; Betz, G. Ultra-short laser ablation of metals and semiconductors: Evidence of ultra-fast Coulomb explosion. Appl. Phys. A Mater. Sci. Process. 2006, 83, 333–336. [Google Scholar] [CrossRef]
- Kelly, R.; Miotello, A. Comments on explosive mechanisms of laser sputtering. Appl. Surf. Sci. 1996, 96–98, 205–215. [Google Scholar] [CrossRef]
- Merino, M.; Ahedo, E. Two-dimensional quasi-double-layers in two-electron-temperature, current-free plasmas. Phys. Plasmas 2013, 20, 023502. [Google Scholar] [CrossRef]
- Bulgakov, V.; Bulgakova, N.M. Dynamics of laser-induced plume expansion into an ambient gas during film deposition. J. Phys. D Appl. Phys. 1999, 28, 1710–1718. [Google Scholar] [CrossRef]
- Focsa, C.; Gurlui, S.; Nica, P.; Agop, M.; Ziskind, M. Plume splitting and oscillatory behavior in transient plasmas generated by high-fluence laser ablation in vacuum. Appl. Surf. Sci. 2017, 424, 299–309. [Google Scholar] [CrossRef]
- Jiang, L.; Tsai, H.-L. A plasma model combined with an improved two-temperature equation for ultrafast laser ablation of dielectrics. J. Appl. Phys. 2008, 104, 093101. [Google Scholar] [CrossRef]
- Eliezer, S. Double layers in laser-produced plasmas. Phys. Rep. 1989, 172, 339–407. [Google Scholar] [CrossRef]
- Singh, S.C.; Fallon, C.; Hayden, P.; Mujawar, M.; Yeates, P.; Costello, J.T. Ion flux enhancements and oscillations in spatially confined laser produced aluminum plasmas. Phys. Plasmas 2014, 21, 093113. [Google Scholar] [CrossRef]
- Borowitz, J.L.; Eliezer, S.; Gazit, Y.; Givon, M.; Jackel, S.; Ludmirsky, A.; Salzmann, D.; Yarkoni, E.; Zigler, A.; Arad, B. Temporally resolved target potential measurements in laser-target interactions. J. Phys. D Appl. Phys. 1987, 20, 210–214. [Google Scholar] [CrossRef]
- Irimiciuc, S.; Boidin, R.; Bulai, G.; Gurlui, S.; Nemec, P.; Nazabal, V.; Focsa, C. Laser ablation of (GeSe2)100−x(Sb2Se3)x chalcogenide glasses: Influence of the target composition on the plasma plume dynamics. Appl. Surf. Sci. 2017, 418, 594–600. [Google Scholar] [CrossRef]
- Stoian, R.; Ashkenasi, D.; Rosenfeld, A.; Campbell, E.E.B. Coulomb explosion in ultrashort pulsed laser ablation of Al2O3. Phys. Rev. B 2000, 62, 13167–13173. [Google Scholar] [CrossRef]
- Nica, P.; Agop, M.; Gurlui, S.; Focsa, C. Oscillatory Langmuir probe ion current in laser-produced plasma expansion. EPL 2010, 89, 65001. [Google Scholar] [CrossRef]
- Ludmirsky, A.; Givon, M.; Eliezer, S.; Gazit, Y.; Jackel, S.; Krumbein, A.; Szichman, H. Electro-optical measurements of high potentials in laser produced plasmas with fast time resolution. Laser Part. Beams 1984, 2, 245–250. [Google Scholar] [CrossRef]
- Ludmirsky, A.; Eliezer, S.; Arad, B.; Borowitz, A.; Gazit, Y.; Jackel, S.; Krumbein, A.D.; Salzmann, D.; Szichman, H. Experimental Evidence of Charge Separation (Double Layer) in Laser-Produced Plasmas. IEEE Trans. Plasma Sci. 1985, 13, 132–134. [Google Scholar] [CrossRef]
- Irimiciuc, S.A.; Agop, M.; Nica, P.; Gurlui, S.; Mihaileanu, D.; Toma, S.; Focsa, C. Dispersive effects in laser ablation plasmas. Jpn. J. Appl. Phys. 2014, 53, 116202. [Google Scholar] [CrossRef]
- Boulmer-Leborgne, C.; Benzerga, R.; Perrière, J. Nanoparticle Formation by Femtosecond Laser Ablation. J. Appl. Phys D 2007, 40, 125–140. [Google Scholar]
- Babushok, V.I.; DeLucia, F.C.; Gottfried, J.L.; Munson, C.A.; Miziolek, A.W. Double pulse laser ablation and plasma: Laser induced breakdown spectroscopy signal enhancement. Spectrochim. Acta Part B At. Spectrosc. 2006, 61, 999–1014. [Google Scholar] [CrossRef]




© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Irimiciuc, S.A.; Enescu, F.; Agop, A.; Agop, M. Lorenz Type Behaviors in the Dynamics of Laser Produced Plasma. Symmetry 2019, 11, 1135. https://doi.org/10.3390/sym11091135
Irimiciuc SA, Enescu F, Agop A, Agop M. Lorenz Type Behaviors in the Dynamics of Laser Produced Plasma. Symmetry. 2019; 11(9):1135. https://doi.org/10.3390/sym11091135
Chicago/Turabian StyleIrimiciuc, Stefan Andrei, Florin Enescu, Andrei Agop, and Maricel Agop. 2019. "Lorenz Type Behaviors in the Dynamics of Laser Produced Plasma" Symmetry 11, no. 9: 1135. https://doi.org/10.3390/sym11091135
APA StyleIrimiciuc, S. A., Enescu, F., Agop, A., & Agop, M. (2019). Lorenz Type Behaviors in the Dynamics of Laser Produced Plasma. Symmetry, 11(9), 1135. https://doi.org/10.3390/sym11091135