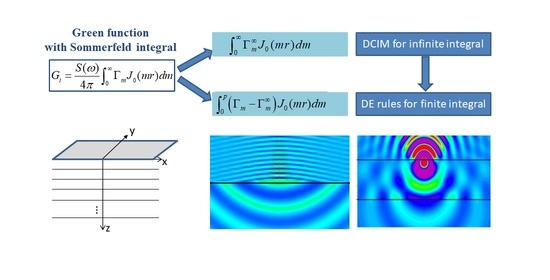
Fast Computation of Green Function for Layered Seismic Field via Discrete Complex Image Method and Double Exponential Rules
Abstract
:1. Introduction
2. Seismic Wave Equation and Green Function
2.1. Seismic Wave Equation
2.2. Green Function in Full-Space
2.3. Green Function in Layered Half-Space
3. Methods
3.1. Partial Closed Form Expression
3.2. ESPRIT Algorithm
3.3. DE Rules
4. Results
4.1. Half-Space
4.2. Three-Layer Model
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Fuchs, K.; Müller, G. Computation of Synthetic Seismograms with the Reflectivity Method and Comparison with Observations. Geophys. J. R. Astron. Soc. 1971, 23, 417–433. [Google Scholar] [CrossRef] [Green Version]
- Yao, Z.; Zheng, T. A Generalized Reflection-transmission Coefficient Matrix and Discrete Wavenumber Method for Synthetic Seismograms (ii)- Multiple sources at Different Depths. Chin. J. Geophys. 1984, 27, 338–348. [Google Scholar]
- Apsel, R.J. Dynamic Green’s functions for layered media and applications to boundary-value problems. Aviat. Week Space Technol. 1979, 125, 209–211. [Google Scholar] [CrossRef] [Green Version]
- Bouchon, M. A simple method to calculate Green’s functions for elastic layered media. Bull. Seism. Soc. Am. 1981, 71, 959–971. [Google Scholar] [CrossRef]
- Olson, A.H. Forward Simulation and Linear Inversion of Earthquake Ground Motions; University of California: San Diego, CA, USA, 1982. [Google Scholar]
- Yao, Z. A generalized reflection-transmission coefficient matrix and discrete wavenumber method for synthetic seismograms. Bull. Seism. Soc. Am. 1983, 73, 647–654. [Google Scholar]
- Karabulut, E.P.; Aksun, M.I. A Novel approach for the Efficient and Accurate Computation of Sommerfeld Integral Tails. In Proceedings of the 2015 International Conference on Electromagnetics in Advanced Applications (ICEAA), Torino, Italy, 7–11 September 2015. [Google Scholar]
- Guo, L. Research and Application of Fast Integral Equation Method Based on Layered Medium Green’s Function. Ph.D. Thesis, School of Electronic Engineering of UESTC, Chengdu, China, 2016. [Google Scholar]
- Press, W.H.; Flannery, B.P.; Teukolsky, S.A.; Vetterling, W.T.; Chipperfield, J.R. Numerical recipes: The art of scientific computing: Cambridge University Press, Cambridge, 1986 (ISBN 0-521-30811-9). xx + 818 pp. Price 25.00. Anal. Chim. Acta. 1987, 199, 293–294. [Google Scholar] [CrossRef]
- Golubovic, R.; Polimeridis, A.G.; Mosig, J.R. Efficient Algorithms for Computing Sommerfeld Integral Tails. IEEE Trans. Antennas Propag. 2012, 60, 2409–2417. [Google Scholar] [CrossRef] [Green Version]
- Niciforovic, R.G.; Polimeridis, A.; Mosig, J.R. Fast Computation of Sommerfeld Integral Tails via Direct Integration Based on Double Exponential-Type Quadrature Formulas. IEEE Trans. Antennas Propag. 2011, 59, 694–699. [Google Scholar] [CrossRef] [Green Version]
- Michalski, K.A.; Mosig, J.R. Efficient computation of Sommerfeld integral tails—Methods and algorithms. J. Electromagn. Waves Appl. 2016, 30, 281–317. [Google Scholar] [CrossRef]
- Mosig, J. The Weighted Averages Algorithm Revisited. IEEE Trans. Antennas Propag. 2012, 60, 2011–2018. [Google Scholar] [CrossRef]
- Michalski, K.A. Extrapolation methods for Sommerfeld integral tails. IEEE Trans. Antennas Propag. 1998, 46, 1405–1418. [Google Scholar] [CrossRef]
- Mosig, J.R.; Gardiol, F.E. A Dynamical Radiation Model for Microstrip Structures. Adv. Electron. Electron Phys. 1982, 59, 139–237. [Google Scholar]
- Takahasi, H.; Mori, M. Double Exponential Formulas for Numerical Integration. Publ. Res. Inst. Math. Sci. 1973, 9, 721–741. [Google Scholar] [CrossRef] [Green Version]
- Rao, Y.; Wang, Y. Fracture effects in seismic attenuation images reconstructed by waveform tomography. Geophysics. 2009, 74, 25. [Google Scholar] [CrossRef]
- Malinowski, M.; Operto, S.; Ribodetti, A. High-resolution seismic attenuation imaging from wide-aperture onshore data by visco-acoustic frequency-domain full-waveform inversion. Geophys. J. Int. 2011, 186, 1179–1204. [Google Scholar] [CrossRef] [Green Version]
- Carpio, A.; Rapún, M.L. Multifrequency Topological Derivative Approach to Inverse Scattering Problems in Attenuating Media. Symmetry 2021, 13, 1702. [Google Scholar] [CrossRef]
- Li, Q. The Way to Precise Exploration: Systematic Engineering Analysis of High Resolution Seismic Exploration; Petroleum Industry Press: Beijing, China, 1994. [Google Scholar]
- Touhei, T. A scattering problem by means of the spectral representation of Green’s function for a layered acoustic half-space. Comput. Mech. 2000, 25, 477–488. [Google Scholar] [CrossRef]
- Faisal, K.M. Improved Matrix Pencil Methods for Parameters Estimation of Plane Wave Signals. Ph.D. Thesis, Department of Electrical Engineering, Pakistan Institute of Engineering & Applied Sciences (PIEAS), Nilore, Islamabad, Pakistan, 2011. [Google Scholar]
- Zhang, X. Modern Signal Processing, 2nd ed.; Tsinghua University Press: Beijing, China, 2002. [Google Scholar]
- Xu, K.; Wang, M. Parameter inversion of acoustic wave equation in frequency domain with Finite element method. Chin. J. Geophys. 2001, 44, 852–864. [Google Scholar] [CrossRef]
- Hua, Y.; Sarkar, T.K. Generalized pencil-of-function method for extracting poles of an EM system from its transient response. IEEE Trans Antennas Propagation. 1989, 37, 229–234. [Google Scholar] [CrossRef] [Green Version]
- Alparslan, A.; Aksun, M.I.; Michalski, K.A. Closed-Form Green’s Functions in Planar Layered Media for All Ranges and Materials. IEEE Trans. Microw. Theory Tech. 2010, 58, 602–613. [Google Scholar] [CrossRef]
- Boix, R.R.; Fructos, A.L.; Mesa, F. Closed-Form Uniform Asymptotic Expansions of Green’s Functions in Layered Media. IEEE Trans. Antennas Propag. 2010, 58, 2934–2945. [Google Scholar] [CrossRef]





| Method | GPOF | ESPRIT |
|---|---|---|
| Computation time | 0.135 s | 0.025 s |
| Method\Parameters | |||
|---|---|---|---|
| DE_WA | 91.2 s | 67.8 s | 57.6 s |
| DE_DCIM | 50.8 s | 38.9 s | 32.5 s |
| Time saving | 44.3% | 42.6% | 43.6% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, S.; Zhou, Z.; Dai, S.; Iqbal, I.; Yang, Y. Fast Computation of Green Function for Layered Seismic Field via Discrete Complex Image Method and Double Exponential Rules. Symmetry 2021, 13, 1969. https://doi.org/10.3390/sym13101969
Liu S, Zhou Z, Dai S, Iqbal I, Yang Y. Fast Computation of Green Function for Layered Seismic Field via Discrete Complex Image Method and Double Exponential Rules. Symmetry. 2021; 13(10):1969. https://doi.org/10.3390/sym13101969
Chicago/Turabian StyleLiu, Siqin, Zhusheng Zhou, Shikun Dai, Ibrar Iqbal, and Yang Yang. 2021. "Fast Computation of Green Function for Layered Seismic Field via Discrete Complex Image Method and Double Exponential Rules" Symmetry 13, no. 10: 1969. https://doi.org/10.3390/sym13101969
APA StyleLiu, S., Zhou, Z., Dai, S., Iqbal, I., & Yang, Y. (2021). Fast Computation of Green Function for Layered Seismic Field via Discrete Complex Image Method and Double Exponential Rules. Symmetry, 13(10), 1969. https://doi.org/10.3390/sym13101969