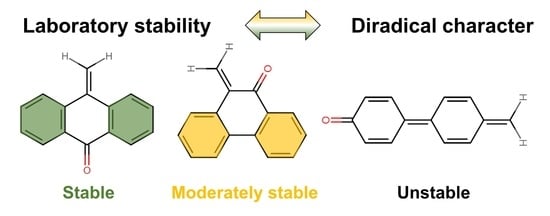
The Interplay between Diradical Character and Stability in Organic Molecules
Abstract
:1. Introduction
2. Materials and Methods
2.1. Molecular Set
2.2. Calculation of the Diradical Character
2.3. Quantum-Chemical Protocol
2.4. Multivariate Analysis
3. Results and Discussion
- (1)
- low DRC (0.114) + high f+max (0.160) = instability (Ia)
- (2)
- low DRC (0.084) + medium-to-high f+max (0.120) = moderate stability (XII)
- (3)
- low DRC (0.074) + low f+max (0.046) = stability (XIb)
- (4)
- medium DRC (0.394) + medium-to-high f+max (0.125) = instability (VIa)
- (5)
- medium DRC (0.508) + low f+max (0.046) = moderate stability (VIb).
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Nakano, M. Electronic structure of open-shell singlet molecules: Diradical character viewpoint. Top. Curr. Chem. 2017, 375, 47. [Google Scholar] [CrossRef] [PubMed]
- Yamaguchi, K. Self-Consistent Field: Theory and Applications; Carbo, R., Klobukowski, M., Eds.; Elsevier: Amsterdam, The Netherlands, 1990; p. 727. [Google Scholar]
- Kamada, K.; Ohta, K.; Shimizu, A.; Kubo, T.; Kishi, R.; Takahashi, H.; Botek, E.; Champagne, B.; Nakano, M. Singlet diradical character from experiment. J. Phys. Chem. Lett. 2010, 1, 937–940. [Google Scholar] [CrossRef]
- Minami, T.; Nakano, M. Diradical character view of singlet fission. J. Phys. Chem. Lett. 2012, 3, 145–150. [Google Scholar] [CrossRef]
- Minami, T.; Ito, S.; Nakano, M. Fundamental of diradical-character-based molecular design for singlet fission. J. Phys. Chem. Lett. 2013, 4, 2133–2137. [Google Scholar] [CrossRef]
- Nakano, M.; Champagne, B. Theoretical design of open-shell singlet molecular systems for nonlinear optics. J. Phys. Chem. Lett. 2015, 6, 3236–3256. [Google Scholar] [CrossRef] [Green Version]
- Nakano, M.; Champagne, B. Nonlinear optical properties in open-shell molecular systems. WIREs Comput. Mol. Sci. 2016, 6, 198–210. [Google Scholar] [CrossRef] [Green Version]
- Nakano, M. Excitation Energies and Properties of Open-Shell Singlet Molecules: Application to a New Class of Molecules for Nonlinear Optics and Singlet Fission; Springer: Cham, Switzerland, 2014. [Google Scholar]
- Takamuku, S.; Nakano, M. Theoretical study on second hyperpolarizabilites of intramolecular pancake-bonded diradicaloids with helical scaffolds. ACS Omega 2019, 4, 2741–2749. [Google Scholar] [CrossRef] [Green Version]
- Nakano, M.; Minami, T.; Yoneda, K.; Muhammad, S.; Kishi, R.; Shigeta, Y.; Kubo, T.; Rougier, L.; Champagne, B.; Kamada, K.; et al. Giant enhancement of the second hyperpolarizabilites of open-shell singlet polyaromatic diphenalenyl diradicaloids by an external electric field and donor-acceptor substitution. J. Phys. Chem. Lett. 2011, 2, 1094–1098. [Google Scholar] [CrossRef]
- Nakano, M.; Champagne, B. Diradical character dependences of the first and second hyperpolarizabilites of asymmetric open-shell singlet systems. J. Chem. Phys. 2013, 138, 244306. [Google Scholar] [PubMed]
- Matsui, H.; Yamane, M.; Tonami, T.; Nakano, M.; de Wergifosse, M.; Seidler, T.; Champagne, B. Theoretical study on third-order nonlinear optical property of one-dimensional cyclic thiazyl aggregates: Intermolecular distance, open-shell nature, and spin-state dependences. J. Phys. Chem. C 2018, 122, 6779–6785. [Google Scholar] [CrossRef]
- Stoycheva, J.; Romanova, J.; Tadjer, A. Women in singlet fission world: Pearls in a semi-open shell. Molecules 2021, 26, 2922. [Google Scholar] [CrossRef]
- Ito, S.; Minami, T.; Nakano, M. Diradical character based design for singlet fission of condensed-ring systems with 4nπ electrons. J. Phys. Chem. C 2012, 116, 19729–19736. [Google Scholar] [CrossRef]
- Ito, S.; Nakano, M. Theoretical molecular design of heteroacenes for singlet fission: Tuning the diradical character by modifying π-conjugation length and aromaticity. J. Phys. Chem. C 2015, 119, 148–157. [Google Scholar] [CrossRef]
- Stoycheva, J.; Tadjer, A.; Garavelli, M.; Spassova, M.; Nenov, A.; Romanova, J. Boron-doped polycyclic aromatic hydrocarbons: A molecular set revealing the interplay between topology and singlet fission propensity. J. Phys. Chem. Lett. 2020, 11, 1390–1396. [Google Scholar] [CrossRef]
- Smith, M.B.; Michl, J. Singlet fission. Chem. Rev. 2010, 110, 6891–6936. [Google Scholar] [CrossRef] [PubMed]
- Zaykov, A.; Felkel, P.; Buchanan, E.A.; Jovanovic, M.; Havenith, R.W.A.; Kathir, R.K.; Broer, R.; Havlas, Z.; Michl, J. Singlet fission rate: Optimized packing of a molecular pair. Ethylene as a model. J. Am. Chem. Soc. 2019, 141, 17729–17743. [Google Scholar] [CrossRef]
- Ryerson, J.L.; Zaykov, A.; Suarez, L.E.A.; Havenith, R.W.A.; Stepp, B.R.; Dron, P.I.; Kaleta, J.; Akdag, A.; Teat, S.J.; Magnera, T.F.; et al. Structure and photophysics of indigoids for singlet fission: Cibalackrot. J. Chem. Phys. 2019, 151, 184903. [Google Scholar] [CrossRef] [PubMed]
- Karlsson, J.K.G.; Atahan, A.; Harriman, A.; Tojo, S.; Fujitsuka, M.; Majima, T. Pulse radiolysis of TIPS-pentacene and a fluorene-bridged bis(pentacene): Evidence for intramolecular singlet-exciton fission. J. Phys. Chem. Lett. 2018, 9, 3934–3938. [Google Scholar] [CrossRef]
- Karlsson, J.K.G.; Atahan, A.; Harriman, A.; Tkachenko, N.V.; Ward, A.D.; Schaberle, F.A.; Serpa, C.; Arnaut, L.G. Singlet exciton fission and associated enthalpy changes with a covalently linked bichromophore comprising TIPS-pentacenes held in an open conformation. J. Phys. Chem. A 2021, 125, 1184–1197. [Google Scholar] [CrossRef]
- Stuyver, T.; Chen, B.; Zeng, T.; Geerlings, P.; de Proft, F.; Hoffmann, R. Do diradicals behave like diradicals? Chem. Rev. 2019, 119, 11291–11351. [Google Scholar] [CrossRef] [PubMed]
- IUPAC. Compendium of Chemical Terminology, 2nd ed.; (The “Gold Book”); McNaught, A.D., Wilkinson, A., Eds.; Blackwell Scientific Publications: Oxford, UK, 1997. [Google Scholar]
- Musil, L.; Koutek, B.; Pišová, M.; Souček, M. Delocalization and stability of o- and p-quinone methides: A HMO study. Collect. Czech. Commun. 1981, 46, 1148–1159. [Google Scholar] [CrossRef]
- Malmqvist, P.A.; Rendell, A.; Roos, B.O. The restricted active space self-consistent-field method, implemented with a split graph unitary group approach. J. Phys. Chem. 1990, 94, 5477–5482. [Google Scholar] [CrossRef]
- Weinhold, F.; Landis, C.R. Discovering Chemistry With Natural Bond Orbitals; John Wiley & Sons: Hoboken, NJ, USA, 2012. [Google Scholar]
- Becke, A.D. Density-functional thermochemistry. III. The role of exact exchange. J. Chem. Phys. 1993, 98, 5648–5652. [Google Scholar]
- Lee, C.; Yang, W.; Parr, R.G. Development of the Colle-Salvetti correlation-energy formula into a functional of the electron density. Phys. Rev. B 1998, 37, 785–789. [Google Scholar] [CrossRef] [Green Version]
- Vosko, S.H.; Wilk, L.; Nusair, M. Accurate spin-dependent electron liquid correlation energies for local spin density calculations: A critical analysis. Can. J. Phys. 1980, 58, 1200–1211. [Google Scholar] [CrossRef] [Green Version]
- Stephens, P.J.; Devlin, F.J.; Chabalowski, C.F.; Frisch, M.J. Ab initio calculation of vibrational absorption and circular dichroism spectra using DFT force fields. J. Phys. Chem. 1994, 98, 11623–11627. [Google Scholar] [CrossRef]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Mennucci, B.; Petersson, G.A.; et al. Gaussian 09, Revision E.01; Gaussian, Inc.: Wallingford, CT, USA, 2009. [Google Scholar]
- Geerlings, P.; de Proft, F.; Langenaeker, W. Conceptual density functional theory. Chem. Rev. 2003, 103, 1793–1874. [Google Scholar] [CrossRef] [PubMed]
- Lu, T.; Chen, F. Multiwfn: A multifunctional wavefunction analyzer. J. Comput. Chem. 2012, 33, 580–592. Available online: http://sobereva.com/multiwfn/ (accessed on 5 December 2019). version 3.7. [CrossRef] [PubMed]
- Clar, E. The Aromatic Sextet; John Wiley & Sons: New York, NY, USA, 1972. [Google Scholar]
- Zeni, C.; Rossi, K.; Glielmo, A.; de Gironcoli, S. Compact atomic descriptors enable accurate predictions via linear models. J. Chem. Phys. 2021, 154, 224112. [Google Scholar] [CrossRef]
- Artrith, N. Machine learning for the modeling of interfaces in energy storage and conversion materials. J. Phys. Energy 2019, 1, 032002. [Google Scholar] [CrossRef]
- Schleder, G.R.; Padilha, A.C.M.; Acosta, C.M.; Costa, M.; Fazzio, A. From DFT to machine learning: Resent approaches to materials science—A review. J. Phys. Mater. 2019, 2, 032001. [Google Scholar] [CrossRef]
- Massart, D.L.; Kaufman, L. The Interpretation of Analytical Chemical Data by the Use of Cluster Analysis; John Wiley and Sons: New York, NY, USA, 1983. [Google Scholar]
- Vandeginste, B.; Massart, D.; de Jong, S.; Buydens, L. Handbook of Chemometrics and Qualimetrics: Part B; Elsevier: Amsterdam, The Netherlands, 1998. [Google Scholar]
- Hill, T.; Lewicki, P. STATISTICS: Methods and Applications; StatSoft, Inc.: Tulsa, OK, USA, 2007. [Google Scholar]
- Clar, E.; Kemp, W.; Stewart, D. The significance of Kekulé structures for the stability of aromatic systems. Tetrahedron 1958, 3, 325–333. [Google Scholar] [CrossRef]
- Witek, H.A. Zhang-Zhang polynomials of multiple zigzag chains revisited: A connection with the John-Sachs theorem. Molecules 2021, 26, 2524. [Google Scholar] [CrossRef] [PubMed]





| Global (B3LYP/6-31G*) | Local (B3LYP/6-31G*) with Hirschfeld Charges | ||
|---|---|---|---|
| I = E(N−1) − E(N) | Vertical ionization potential | f+max | Largest atomic Fukui index for nucleophilic attack |
| A = E(N) − E(N+1) | Vertical electron affinity | f−max | Largest atomic Fukui index for electrophilic attack |
| ƞ = ELUMO − EHOMO | Hardness | f°max | Largest atomic Fukui index for radical attack |
| δ = | Softness | ||
| χ = − (EHOMO + ELUMO) | Electronegativity | ||
| ω = | Electrophilicity | ||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Petakova, V.; Nedyalkova, M.; Stoycheva, J.; Tadjer, A.; Romanova, J. The Interplay between Diradical Character and Stability in Organic Molecules. Symmetry 2021, 13, 1448. https://doi.org/10.3390/sym13081448
Petakova V, Nedyalkova M, Stoycheva J, Tadjer A, Romanova J. The Interplay between Diradical Character and Stability in Organic Molecules. Symmetry. 2021; 13(8):1448. https://doi.org/10.3390/sym13081448
Chicago/Turabian StylePetakova, Vaska, Miroslava Nedyalkova, Joanna Stoycheva, Alia Tadjer, and Julia Romanova. 2021. "The Interplay between Diradical Character and Stability in Organic Molecules" Symmetry 13, no. 8: 1448. https://doi.org/10.3390/sym13081448
APA StylePetakova, V., Nedyalkova, M., Stoycheva, J., Tadjer, A., & Romanova, J. (2021). The Interplay between Diradical Character and Stability in Organic Molecules. Symmetry, 13(8), 1448. https://doi.org/10.3390/sym13081448