Anonymous Multi-Receiver Identity-Based Authenticated Encryption with CCA Security
Abstract
:1. Introduction
Anonymous Multi-Receiver ID-Based Encryption vs. Anonymous Dynamic Broadcast ID-Based Encryption
2. Related Works
3. Preliminaries
- -
- Setup is an algorithm that takes as input a security parameter l. It returns a master secret key and system parameters .
- -
- KeyExtract is an algorithm that takes as input , and a user’s identity and then returns the secret key of the user.
- -
- Encrypt is an algorithm that takes as input , a message M, the identity of the sender, the private key of the sender and an identity set and returns a ciphertext C. We write .
- -
- Decrypt is an algorithm that takes as input , a ciphertext C and the secret key of user and returns a message M. We write .
- Randomly choose , and compute .
- Compute .
- Set the M-DBDH instance as , and input it into .
4. Our Scheme
| Notation | Meaning |
|---|---|
| a cyclic additive group of prime order q | |
| a cyclic multiplicative group of prime order q | |
| e | a bilinear mapping; |
| P | a generator of |
| KGC | the key generation center |
| the public key of KGC | |
| M | a message |
| the identity of user i | |
| the hashed value of | |
| the private key of |
- SetupThe key generation center (KGC) performs the following operations:
- Choose an integer randomly as the master secret key, and set .
- Choose three cryptographic one-way hash functions, , , and .
- Compute .
- Publish the system parameters and keep the master key α secret.
- KeyExtractWhen user i joins the system, KGC will compute and the private key of the user, and then, KGC will send to user i in a secure manner.
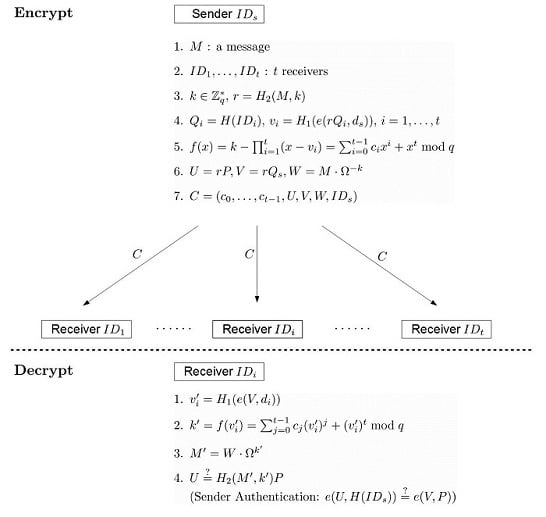
- EncryptA sender, say , produces the ciphertext of a message by performing the following steps:
- Choose a message , and select a set of t receivers .
- Choose at random, and compute .
- For to t, compute and .
- Compute .
- Compute and .
- Set the ciphertext .
- DecryptAfter receiving the ciphertext , a selected receiver, say , can decrypt C as follows.
- Compute .
- Compute .
- Compute .
- Accept if . If the receiver wants to authenticate the identity of the sender, he can check whether .

5. Security Models and Proofs
- -
- Hash query: operates hash functions on the inputs given by and returns the hashed values.
- -
- KeyExtract (): sends an identity to and returns the private key of where KeyExtract () cannot be queried if .
- -
- Encrypt (): sends a sender’s identity , a receiver set and a message M to . returns a ciphertext C to .
- -
- Decrypt (): sends an identity and a ciphertext C to , and returns the message M.

- -
- Hash query: operates hash functions on the inputs given by and returns the hashed values.
- -
- KeyExtract (): sends an identity to , and returns the private key of where neither KeyExtract () nor KeyExtract () can be queried.
- -
- Encrypt (): sends a sender’s identity , a receiver set and a message M to . returns a ciphertext C to .
- -
- Decrypt (): sends an identity and a ciphertext C to , and returns the message M.

- -
- Hash query: operates hash functions on the inputs given by and returns the hashed values.
- -
- KeyExtract (): sends an identity to and returns the private key of where neither KeyExtract () nor KeyExtract () can be queried.
- -
- Encrypt (): sends a sender’s identity , a receiver set and a message M to . returns a ciphertext C to .
- -
- Decrypt (): sends an identity and a ciphertext C to , and returns the message M.

- -
- H-query:This oracle takes an identity as input. If there exists a record in H-list, return . Otherwise, do the following:
- Randomly select .
- If , compute ; else .
- Return , and add into H-list.
- -
- -query:This oracle takes as input, where . If there exists a record in -list, return . Otherwise, do the following:
- Randomly choose .
- Add to -list.
- Return .
- -
- -query:This oracle takes and an integer as input. If there exists a record in -list, return . Otherwise, do the following:
- Randomly choose , and compute .
- Add to -list.
- Return .
- -
- KeyExtract:This oracle takes an identity as input. Call and retrieve from H-list. Then, does the following:
- -
- If , return “reject”.
- -
- Otherwise, compute and return .
- -
- Encrypt:This oracle takes identities and a message M as input. Upon receiving an Encryptquery, does the following:
- Choose at random, and set .
- For to u,
- -
- if , compute , where is the private key of the sender ;
- -
- if and , compute , where is the private key of the receiver ;
- -
- if , compute .
- Compute .
- Compute and .
- Set the ciphertext , and return C.
- -
- Decrypt:This oracle takes an identity and a ciphertext C as input. Upon receiving a Decryptquery, denoted by Decrypt where , does the following:
- Search -list to get with . If not found, return “reject”.
- Search H-list to get with . If not found, return “reject”.
- This step can be separated into three cases:
- -
- if , compute ;
- -
- if and , compute ;
- -
- if , compute .
- Compute .
- Check whether and or not. If not, return “reject”. Otherwise, return .
- Choose randomly.
- For to t, call , and retrieve from H-list.
- Call , and retrieve from H-list.
- Choose , and set and .
- For to t, compute .
- Compute and .
- Set the ciphertext , and send to .
- Choose randomly.
- For to t, call , and retrieve from H-list.
- Call , and retrieve from H-list.
- Call , and retrieve from H-list.
- Choose , and set and .
- For to t, compute .
- Compute .
- Compute and .
- Set the ciphertext and send to .
- -
- H-query:This oracle takes an identity as input. If there exists a record in H-list, return . Otherwise, do the following:
- Randomly select .
- If , compute ; else if , compute ; else .
- Return and add into H-list.
- -
- The simulation of -query and -query are the same as those in the proof of Theorem 13.
- -
- KeyExtract:This oracle takes an identity as input. Call , and retrieve from H-list. Then, does the following:
- -
- If , return “reject”.
- -
- Otherwise, compute , and return .
- -
- Encrypt:This oracle takes identities and a message M as input. Upon receiving an Encrypt query, does the following:
- Choose at random, and set .
- For to u,
- -
- if , compute , where is the private key of the sender ;
- -
- if and , compute , where is the private key of the receiver ;
- -
- if , compute .
- Compute .
- Compute and .
- Set the ciphertext , and return C.
- -
- Decrypt:This oracle takes an identity and a ciphertext C as input. Upon receiving a Decrypt query, denoted by Decrypt , where , does the following:
- Search -list to get with . If not found, return “reject”.
- Search H-list to get with . If not found, return “reject”.
- This step can be separated into three cases:
- -
- if , compute ;
- -
- if and , compute ;
- -
- if , compute .
- Compute .
- Check whether and or not. If not, return “reject”. Otherwise, return .
- Search -list to get with .
- Call and to retrieve and from H-list.
- Compute .
- Compute .
- Check whether and or not. If it is, wins the game.
- : The game has been correctly simulated.
- : wins the game.
6. Comparisons
| Encryption Cost | Decryption Cost | Ciphertext Length | |
|---|---|---|---|
| [10] | |||
| [11] | |||
| [25] | |||
| [21] | |||
| [18] | |||
| [16] | |||
| [29] | |||
| [31]-Scheme 1 | |||
| [31]-Scheme 2 | |||
| [14] | |||
| [19] | |||
| [28] | |||
| [20] | |||
| [23] | |||
| [27] | |||
| [26] | |||
| Ours | |||
| Confidentiality | Anonymity | SecurityModel | Sender Authentication | ||
|---|---|---|---|---|---|
| Outsider | Insider | ||||
| [10] | CCA | △ | △ | ROM | No |
| [11] | – | – | – | – | No |
| [25] | CCA | CCA | △ | ROM | No |
| [21,22] | △ | △ | △ | ROM | No |
| [18] | CPA | CPA | CPA | ROM | No |
| [29] | – | – | – | – | No |
| [16] | CPA | CPA | CPA | ROM | No |
| [31]-Scheme 1 | CCA | CCA | △ | ROM | No |
| [31]-Scheme 2 | – | – | – | – | No |
| [14] | CPA | CPA | CPA | ROM | No |
| [19] | CPA | – | – | ROM | No |
| [28] | △ | △ | △ | ROM | No |
| [20] | CPA | CPA | CPA | STD | No |
| [23] | △ | △ | △ | ROM | No |
| [27] | △ | △ | △ | ROM | Yes |
| [26] | – | △ | △ | ROM | No |
| Ours | CCA | CCA | CCA | ROM | Yes |
7. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Appendix
A.1. Cryptanalysis to Other AMRIBEs
| Notation | Meaning |
|---|---|
| a cyclic groups of prime order q | |
| a cyclic groups of prime order q | |
| e | a bilinear mapping; |
| P | a generator of |
| KGC | the key generation center |
| the public key of KGC | |
| M | the message that the sender wants to send |
| a secure symmetric encryption scheme with secret key k | |
| the hash value of |
A.1.1. Comment on Tseng et al.’S Scheme [21,22]
Comments
A.1.2. Comment on Tseng et al.’s Scheme [23]
A.1.3. Comment on Zhang et al.’s Scheme [27]
A.1.4. Comment on Zhang et al.’s Scheme [28]
Comments
A.1.5. Comment on Wang’s Scheme [26]
The Simulation of the CCA Game for Confidentiality
Comments
- Choose a receiver set , where is the target identity.
- Choose to compute and as that in the algorithm of their scheme.
- Choose , and compute , .
- Query .
- Set and .
References
- Arul, T.; Shoufan, A. Consumer Opinions on Short-Interval Charging for Pay-TV over IPTV. In Proceedings of the 26th International Conference on Advanced Information Networking and Applications Workshops (WAINA), Fukuoka, Japan, 26–29 March 2012; pp. 147–153.
- Msgna, M.G.; Markantonakis, K.; Mayes, K.; Akram, R.N. Subscriber Centric Conditional Access System for Pay-TV Systems. In Proceedings of the 2013 IEEE 10th International Conference on e-Business Engineering (ICEBE), Coventry, UK, 11–13 September 2013; pp. 450–455.
- Liu, Y.; Duan, J.; Tang, Q.; Zhang, Y. A Simple and Efficient Re-Scrambling Scheme for DTV Programs. IEEE Trans. Multimed. 2014, 16, 137–146. [Google Scholar] [CrossRef]
- Baek, J.; Safavi-Naini, R.; Susilo, W. Efficient Multi-Receiver Identity-Based Encryption and Its Application to Broadcast Encryption. In Proceedings of the 8th International Conference on Theory and Practice in Public Key Cryptography, Les Diablerets, Switzerland, 23–26 January 2005; pp. 380–397.
- Wang, L.; Wu, C.K. Efficient identity-based multicast scheme from bilinear pairing. IEEE Proc. Commun. 2005, 152, 877–882. [Google Scholar] [CrossRef]
- Du, X.; Wang, Y.; Ge, J.; Wang, Y. An ID-based broadcast encryption scheme for key distribution. IEEE Trans. Broadcast. 2015, 51, 264–266. [Google Scholar] [CrossRef]
- Boneh, D.; Franklin, M. Identity-based encryption from the weil pairing. In Proceedings of the 21st Annual International Cryptology Conference, Santa Barbara, CA, USA, 19–23 August 2001; pp. 213–229.
- Bellare, M.; Rogaway, P. Random Oracles Are Practical: A Paradigm for Designing Efficient Protocols. In Proceedings of the 1st ACM Conference on Compute and Communications Security, Fairfax, VA, USA, 3–5 November 1993; pp. 62–73.
- Okamoto, T.; Pointcheval, D. REACT: Rapid Enhenced-Security Asymmetric Cryptosystem Transform. In Topics in Cryptology CT-RSA 2001; Springer-Verlag Berling Heiderlberg: New York, NY, USA, 2001; pp. 159–175. [Google Scholar]
- Fan, C.I.; Huang, L.Y.; Ho, P.H. Anonymous Multireciever identity-based encryption. IEEE Trans. Comput. 2010, 59, 1239–1249. [Google Scholar] [CrossRef]
- Chien, H.Y. Improved anonymous multi-receiver identity-based encryption. Comput. J. 2012, 55, 439–446. [Google Scholar] [CrossRef]
- Chen, Z.; Li, S.; Wang, C.; Shen, Y. Two constructions of multireceiver encryption supporting constant keys, short ciphertexts, and identity privacy. Int. J. Netw. Secur. 2012, 14, 270–279. [Google Scholar]
- Chen, Z.; Li, S.; Wang, C.; Zhang, M. Comments on FHH anonymous multireceiver encryption. Int. J. Netw. Secur. 2014, 16, 285–288. [Google Scholar]
- Cui, H.; Mu, Y.; Guo, F. Server-aided identity-based anonymous broadcast encryption. Int. J. Netw. Secur. 2013, 8, 29–39. [Google Scholar] [CrossRef]
- Harn, L.; Chang, C.C.; Wu, H.L. An anonymous multi-receiver encryption based on RSA. Int. J. Netw. Secur. 2013, 15, 307–312. [Google Scholar]
- Hur, J.; Park, C.; Hwang, S.O. Privacy-preserving identity-based broadcast encryption. Inf. Fusion 2012, 13, 296–303. [Google Scholar] [CrossRef]
- Li, H.; Pang, L. Cryptanalysis of Wang et al’s improved anonymous multi-receiver identity-based encryption scheme. IET Inf. Secur. 2013, 8, 8–11. [Google Scholar] [CrossRef]
- Muthulakshmi, A.; Anitha, R.; Rohini, S.; Princy, K. Identity Based Privacy Preserving Dynamic Broadcast Encryption for multi-privileged group. In Recent Trends in Computer Networks and Distributed Systems Security; Spring: Berlin Heidelberg, Germany, 2012; Volume 335, pp. 272–282. [Google Scholar]
- Pang, L.; Guo, L.; Pei, Q.; Gui, J.; Wang, Y. A new ID-based multi-recipient public-key Encryption Scheme. Chin. J. Electron. 2013, 22, 89–92. [Google Scholar]
- Ren, Y.; Niu, Z.; Zhang, X. Fully anonymous identity-based broadcast encryption without random oracles. Int. J. Netw. Secur. 2014, 16, 256–264. [Google Scholar]
- Tseng, Y.M.; Huang, Y.H.; Chang, H.J. Privacy-preserving multireceiver ID-based encryption with provable security. Int. J. Commun. Syst. 2014, 27, 1034–1050. [Google Scholar] [CrossRef]
- Tseng, Y.M.; Huang, Y.H.; Chang, H.J. CCA-Secure Anonymous Multi-Receiver ID-Based Encryption. In 26th International Conference on Advanced Information Networking and Applications Workshops, Fukuoka, Japan, 26–29 March 2012; pp. 177–182.
- Tseng, Y.M.; Tsai, T.T.; Huang, S.S.; Chien, H.Y. Efficient anonymous multi-receiver ID-based encryption with constant decryption cost. In Proceedings of the 2014 International Conference on Information Science, Electronics and Electrical Engineering (ISEEE), Sapporo, Japan, 26–28 April 2014; pp. 131–137.
- Wang, H. Insecurity of “Improved Anonymous Multi-Receiver Identity-Based Encryption”. Comput. J. 2013. [Google Scholar] [CrossRef]
- Wang, H.; Zhang, Y.; Xiong, H.; Qing, B. Crytanalysis and improvements of an anonymous multi-receiver identity-based encryption scheme. IET Inf. Secur. 2012, 6, 20–27. [Google Scholar] [CrossRef]
- Wang, H. Provably Secure Anonymous Multi-receiver Identity-Based Encryption with Shorter Ciphertext. In Proceedings of the 2014 IEEE 12th International Conference on Dependable, Autonomic and Secure Computing (DASC), Dalian, China, 24–27 August 2014; pp. 85–90.
- Zhang, B.; Sun, T.; Yu, D. ID-Based Anonymous Multi-Receiver Key Encapsulation Mechanism with Sender Authentication. In Algorithm and Architectures for Parallel Processing; Lecture Notes in Computer Science; Springer-Verlag Berlin Heidelberg: New York, NY, USA, 2014; Volume 8631, pp. 645–658. [Google Scholar]
- Zhang, J.; Mao, J. An improved anonymous multi-receiver identity-based encryption Scheme. Int. J. Commun. Syst. 2015, 28, 645–658. [Google Scholar] [CrossRef]
- Zhang, J.; Xu, Y. Comment on Anonymous Multi-Receiver Identity-Based Encryption Scheme. In Proceedings of the 4th International Conference on Intelligent Networking and Collaborative Systems, Barcelona, Spain, 19–21 September 2012; pp. 473–476.
- Zhang, J.; Xu, Y.; Zou, J. Comment on Wang et al.’s anonymous multi-receiver ID-based encryption scheme and its improved schemes. Int. J. Intell. Inf. Database Syst. 2013, 7, 400–413. [Google Scholar] [CrossRef]
- Zhang, M.; Takagi, T. Efficient constructions of anonymous multireceiver encryption protocol and their deployment in group E-Mail systems with privacy preservation. IEEE Syst. J. 2013, 7, 410–419. [Google Scholar] [CrossRef]
- Delerablée, C.; Paillier, P.; Pointcheval, D. Fully Collusion Secure Dynamic Broadcast Encryption with Constant-Size or Decryption Keys. In Pairing-Based Cryptography—Pairing 2007; Takagi, T., Ed.; Springer: Berlin, Germany, 2007; Volume 4575, pp. 39–59. [Google Scholar]
- Delerablée, C. Identity-Based Broadcast Encryption with Constant Size Ciphertexts and Private Keys. In Advances in Cryptology-EUROCRYPT 2007; Springer: Berlin Heidelberg, Germany, 2007; pp. 200–215. [Google Scholar]
- Nelly, F.; Perera, I.M. Outsider-Anonymous Broadcast Encryption with Sublinear Ciphertexts. In Proceedings of the 15th International Conference on Practice and Theory in Public Key Cryptography, Darmstadt, Germany, 21–23 May 2012; pp. 225–242.
- Zhang, L.; Wu, Q.; Mu, Y. Anonymous Identity-Based Broadcast Encryption with Adaptive Security. In Proceedings of the 5th International Symposium, CSS 2013, Zhangjiajie, Hunan, China, 13–15 November 2013; pp. 258–271.
- Libert, B.; Paterson, K.G.; Quaglia, E.A. Anonymous Broadcast Encryption: Adaptive Security and Efficient Construction in the Standard Model. In Proceedings of the 15th International Conference on Practice and Theory in Public Key Cryptography, Darmstadt, Germany, 21–23 May 2012; pp. 225–242.
- Boneh, D.; Boyen, X.; Goh, E.J. Hierarchical Identity Based Encryption with Constant Size Ciphertext. In Advances in Cryptology-EUROCRYPT 2005; Springer: Berlin Heidelberg, Germany, 2005; pp. 440–456. [Google Scholar]
- Kiayias, A.; Samari, K. Lower Bound for Private Broadcast Encryption. In Information Hiding; Springer: Berlin/Heidelberg, Germany, 2013; pp. 176–190. [Google Scholar]
- Neal, K.; Alfred, M.; Vanstone, S. The state of elliptic curve cryptography. Des. Codes Cryptogr. 2000, 19, 173–193. [Google Scholar]
- Menezes, A.J.; Vanstone, S.A.; van Oorschot, P.C. Handbook of Applied Cryptography; CRC Press, Inc.: Boca Raton, FL, USA, 2001. [Google Scholar]
- Scott, M. Implementing Cryptographic Pairings. In Proceedings of the Pairing-Based Cryptography, Tokyo, Japan, 2–4 July 2007; pp. 177–196.
- Zhang, Y.; Liu, W.; Lou, W.; Fang, Y. Securing mobile Ad Hoc networks with certificateless public keys. IEEE Trans. Depend. Secur. Comput. 2006, 3, 386–399. [Google Scholar] [CrossRef]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fan, C.-I.; Tseng, Y.-F. Anonymous Multi-Receiver Identity-Based Authenticated Encryption with CCA Security. Symmetry 2015, 7, 1856-1881. https://doi.org/10.3390/sym7041856
Fan C-I, Tseng Y-F. Anonymous Multi-Receiver Identity-Based Authenticated Encryption with CCA Security. Symmetry. 2015; 7(4):1856-1881. https://doi.org/10.3390/sym7041856
Chicago/Turabian StyleFan, Chun-I, and Yi-Fan Tseng. 2015. "Anonymous Multi-Receiver Identity-Based Authenticated Encryption with CCA Security" Symmetry 7, no. 4: 1856-1881. https://doi.org/10.3390/sym7041856
APA StyleFan, C. -I., & Tseng, Y. -F. (2015). Anonymous Multi-Receiver Identity-Based Authenticated Encryption with CCA Security. Symmetry, 7(4), 1856-1881. https://doi.org/10.3390/sym7041856