Breakage Characterization of Grinding Media Based on Energy Consumption and Particle Size Distribution: Hexagons versus Cylpebs
Abstract
:1. Introduction
2. Materials and Methods
2.1. Materials and Grinding Media
2.2. Experimental Methods
2.3. Confidence Analysis of Experiments
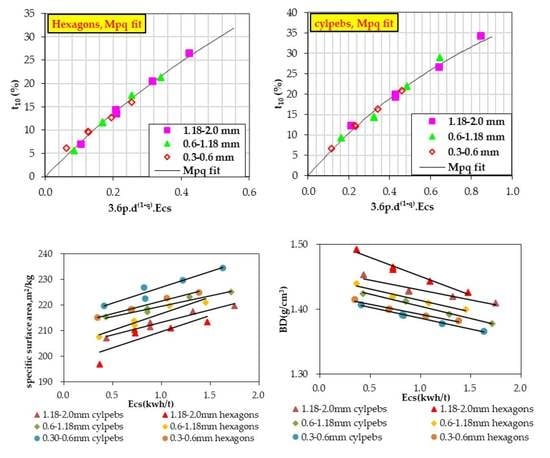
3. Results and Discussion
3.1. Size Distribution Characterization of Ground Product
3.2. Energy Consumption Characterization of the Grinding Process
3.3. Relationship between Specific Surface Area and Energy Consumption
3.4. Relationship between Bulk Density and Energy Consumption
3.5. Distribution Characteristics of Particle Size Uniformity
3.6. Validation Using Tungsten Ore
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Norris, C.C. Some grinding tests with spheres and other shapes. Trans. IMM 1953, 63, 197–209. [Google Scholar]
- Duan, X.X. Selective Grinding and Its Application; Metallurgical Industry Press: Beijing, China, 1991. (In Chinese) [Google Scholar]
- Wu, C.B. Research on the Application of Crushing Statistical Mechanics Principle and Transition Probability. In The System of Ball Filling; Kunming University of Science and Technology: Kunming, China, 2002. (In Chinese) [Google Scholar]
- Cloos, U. Cylpebs: An alternative to balls as grinding media. World Min. 1983, 36, 59. [Google Scholar]
- Kiangi, K.; Potapov, A.; Moys, M. DEM validation of media shape effects on the load behaviour and power in a dry pilot mill. Miner. Eng. 2013, 46–47, 52–59. [Google Scholar] [CrossRef]
- Herbst, J.A.; LO, Y.C. Grinding Efficiency with Balls or Cones as Media. Int. J. Miner. Process. 1989, 26, 141–151. [Google Scholar] [CrossRef]
- Von Kfuger, F.L.; Donda, J.D.; Drummond, M.A.R.; Peres, A.E.C. The effect of using concave surfaces as grinding media. Dev. Miner. Process. 2000, 13, C4-86–C4-93. [Google Scholar]
- Shi, F. Comparison of grinding media—Cylpebs versus balls. Miner. Eng. 2004, 17, 1259–1268. [Google Scholar] [CrossRef]
- Rittinger, P.R. Lehrbuch der Aufbereitungskunde; Ernst & Korn: Berlin, Germany, 1867. (In German) [Google Scholar]
- Kick, F. Das Gesetz der Proportionalen Winderstands and Seine Anwendug; Springer: Leipzig, Germany, 1885. (In German) [Google Scholar]
- Bond, F.C. The third theory of comminution. Trans. AIME 1952, 193, 484–494. [Google Scholar]
- Stamboliadis, E.T. Impact crushing approach to the relationship of energy and particle size in comminution. Eur. J. Miner. Process. Environ. Prot. 2003, 3, 160–166. [Google Scholar]
- Stamboliadis, E.T. Energy distribution in comminution, a new approach to the laws of Rittinger, Bond and Kick. Can. Metall. Q. 2004, 43, 249–258. [Google Scholar] [CrossRef]
- Stamboliadis, E.T. The energy distribution theory of comminution specific surface energy, mill efficiency and distribution mode. Miner. Eng. 2007, 20, 140–145. [Google Scholar] [CrossRef]
- Stamboliadis, E.T. Surface area production during grinding. Miner. Eng. 2009, 22, 587–592. [Google Scholar] [CrossRef]
- Shi, G.M.; Zhou, Y.C.; Wu, C.B.; Yang, H.; Zhou, B.; Liu, Y.; Zhao, R.; Zou, C.; Yan, F.; Zhao, J. Double Spherical Hexagonal Prism Grinding Media. CN104888904A, 9 September 2015. [Google Scholar]
- Xie, W.; He, Y.; Ge, Z.; Shi, F.; Yang, Y.; Li, H.; Wang, S.; Li, K. An analysis of the energy split for grinding coal/calcite mixture in a ball-and-race mill. Miner. Eng. 2016, 93, 1–9. [Google Scholar] [CrossRef]
- Li, C.; Gao, Z. Effect of grinding media on the surface property and flotation behavior of scheelite particles. Powder Technol. 2017, 322, 386–392. [Google Scholar] [CrossRef]
- Ulusoy, U.; Kursun, I. Comparison of different 2D image analysis measurement techniques for the shape of talc particles produced by different media milling. Miner. Eng. 2011, 24, 91–97. [Google Scholar] [CrossRef]
- Shi, F.; Kojovic, T. Validation of a model for impact breakage incorporating particle size effect. Int. J. Miner. Process. 2007, 22, 156–163. [Google Scholar] [CrossRef]
- Shi, F.; Kojovic, T.; Brennan, M. Modelling of vertical spindle mills. Part 1: Sub-models for comminution and classification. Fuel 2015, 143, 595–601. [Google Scholar] [CrossRef]
- Shi, F. A review of the applications of the JK size-dependent breakage model Part 1: Ore and coal breakage characterisation. Int. J. Miner. Process. 2016, 155, 118–129. [Google Scholar] [CrossRef]
- Shi, F. A review of the applications of the JK size-dependent breakage model Part 2: Assessment of material strength and energy requirement in size reduction. Int. J. Miner. Process. 2016, 157, 36–45. [Google Scholar] [CrossRef]
- Shi, F. A review of the applications of the JK size-dependent breakage model Part 3: Comminution equipment modelling. Int. J. Miner. Process. 2016, 157, 60–72. [Google Scholar] [CrossRef]
- Standish, N. Optimization of coal grind for maximum bulk density. Powder Technol. 1991, 68, 175–186. [Google Scholar] [CrossRef]















| Grinding Media | Cylpebs | Hexagons |
|---|---|---|
| Dimension (mm) | Φ48 × 36 | Φ48 × 36 |
| Total mass (g) | 10,671 | 10,664 |
| Single mass (g) | 338.12 | 390.5 |
| Surface area (cm2) | 74.61 | 84.49 |
| Specific surface (cm2/g) | 0.22 | 0.22 |
| Grinding media number | 31 | 28 |
| Total surface area (cm2) | 2312.91 | 2365.72 |
| Bulk density (g/cm3) | 4.91 | 4.90 |
| Size | 0.6–0.3 mm | |||
|---|---|---|---|---|
| Grinding Media | Cylpebs | Hexagons | ||
| Ecs (kWh/t) | t10 (%) | Ecs (kWh/t) | t10 (%) | |
| Repeat 1 | 0.82 | 13.67 | 0.69 | 9.36 |
| Repeat 2 | 0.86 | 13.40 | 0.65 | 9.68 |
| Repeat 3 | 0.80 | 13.10 | 0.68 | 9.74 |
| Mean | 0.83 | 13.39 | 0.67 | 9.60 |
| 95% Confidence limit | 0.04 | 0.32 | 0.02 | 0.22 |
| 95% Confidence limit relative to the mean (%) | 4.18 | 2.41 | 3.50 | 2.27 |
| Grinding Media | Production | Yield (%) | Tungsten Grade (%) | Tungsten Recovery (%) |
|---|---|---|---|---|
| Cylpebs | Sulfur concentrate | 5.30 | 0.13 | 1.06 |
| Tungsten concentrate | 49.30 | 1.01 | 76.59 | |
| Tailings | 45.40 | 0.32 | 22.35 | |
| Feed | 100.00 | 0.65 | 100.00 | |
| Hexagons | Sulfur concentrate | 4.59 | 0.08 | 0.56 |
| Tungsten concentrate | 50.03 | 1.02 | 78.50 | |
| Tailings | 45.38 | 0.30 | 20.94 | |
| Feed | 100.00 | 0.65 | 100.00 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, C.; Liao, N.; Shi, G.; Zhu, L. Breakage Characterization of Grinding Media Based on Energy Consumption and Particle Size Distribution: Hexagons versus Cylpebs. Minerals 2018, 8, 527. https://doi.org/10.3390/min8110527
Wu C, Liao N, Shi G, Zhu L. Breakage Characterization of Grinding Media Based on Energy Consumption and Particle Size Distribution: Hexagons versus Cylpebs. Minerals. 2018; 8(11):527. https://doi.org/10.3390/min8110527
Chicago/Turabian StyleWu, Caibin, Ningning Liao, Guiming Shi, and Liangliang Zhu. 2018. "Breakage Characterization of Grinding Media Based on Energy Consumption and Particle Size Distribution: Hexagons versus Cylpebs" Minerals 8, no. 11: 527. https://doi.org/10.3390/min8110527
APA StyleWu, C., Liao, N., Shi, G., & Zhu, L. (2018). Breakage Characterization of Grinding Media Based on Energy Consumption and Particle Size Distribution: Hexagons versus Cylpebs. Minerals, 8(11), 527. https://doi.org/10.3390/min8110527