Bubble Rise Velocity and Surface Mobility in Aqueous Solutions of Sodium Dodecyl Sulphate and n-Propanol
Abstract
:1. Introduction
2. Materials and Methods
3. Results and Discussion
3.1. Surface Tension
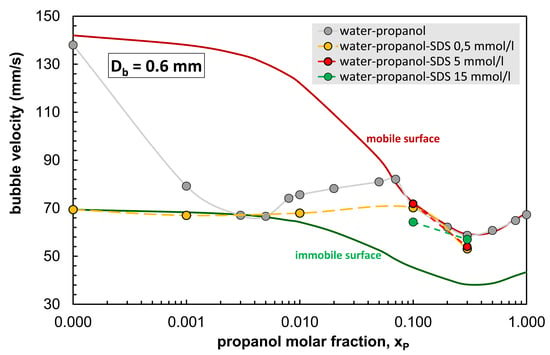
3.2. Terminal Bubble Rise Velocity
3.3. Drag Coefficients and Bubble Surface Mobility
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Dolenko, T.A.; Burikov, S.A.; Dolenko, S.A.; Efitorov, A.O.; Plastinin, I.V.; Yuzhakov, V.I.; Patsaeva, S.V. Raman Spectroscopy of Water-Ethanol Solutions: The Estimation of Hydrogen Bonding Energy and the Appearance of Clathrate-like Structures in Solutions. J. Phys. Chem. A 2015, 119, 10806–10815. [Google Scholar] [CrossRef]
- Lam, R.K.; Smith, J.W.; Saykally, R.J. Communication: Hydrogen bonding interactions in water-alcohol mixtures from X-ray absorption spectroscopy. J. Chem. Phys. 2016, 144. [Google Scholar] [CrossRef] [PubMed]
- Banerjee, S.; Ghosh, R.; Bagchi, B. Structural Transformations, Composition Anomalies and a Dramatic Collapse of Linear Polymer Chains in Dilute Ethanol-Water Mixtures. J. Phys. Chem. B 2012, 116, 3713–3722. [Google Scholar] [CrossRef] [PubMed]
- Dixit, S.; Crain, J.; Poon, W.C.K.; Finney, J.L.; Soper, A.K. Molecular segregation observed in a concentrated alcohol-water solution. Nature 2002, 416, 829–832. [Google Scholar] [CrossRef] [PubMed]
- Takamuku, T.; Maruyama, H.; Watanabe, K.; Yamaguchi, T. Structure of 1-propanol-water mixtures investigated by large-angle X-ray scattering technique. J. Solut. Chem. 2004, 33, 641–660. [Google Scholar] [CrossRef]
- Chodzińska, A.; Zdziennicka, A.; Jańczuk, B. Volumetric and Surface Properties of Short Chain Alcohols in Aqueous Solution–Air Systems at 293 K. J. Solut. Chem. 2012, 41, 2226–2245. [Google Scholar] [CrossRef] [PubMed]
- Basarova, P.; Pislova, J.; Mills, J.; Orvalho, S. Influence of molecular structure of alcohol-water mixtures on bubble behaviour and bubble surface mobility. Chem. Eng. Sci. 2018, 192, 74–84. [Google Scholar] [CrossRef]
- Pang, F.M.; Seng, C.E.; Teng, T.T.; Ibrahim, M.H. Densities and viscosities of aqueous solutions of 1-propanol and 2-propanol at temperatures from 293.15 K to 333.15 K. J. Mol. Liq. 2007, 136, 71–78. [Google Scholar] [CrossRef]
- Vazquez, G.; Alvarez, E.; Navaza, J.M. Surface-Tension of Alcohol Plus Water from 20-Degrees-C to 50-Degrees-C. J. Chem. Eng. Data 1995, 40, 611–614. [Google Scholar] [CrossRef]
- Bielawska, M.; Janczuk, B.; Zdziennicka, A. Volumetric properties of sodium dodecylsulfate and Triton X-100 mixture with short-chain alcohol in aqueous solution. Coll. Surf. A 2015, 480, 270–278. [Google Scholar] [CrossRef]
- Bielawska, M.; Janczuk, B.; Zdziennicka, A. Influence of short chain alcohols on adsorption of sodium dodecylsulfate and Triton X-100 mixture at solution-air interface. Colloid Surf. A 2015, 464, 57–64. [Google Scholar] [CrossRef]
- Bhattarai, A.; Chatterjee, S.K.; Deo, T.K.; Niraula, T.P. Effects of Concentration, Temperature, and Solvent Composition on the Partial Molar Volumes of Sodium Lauryl Sulfate in Methanol (1) + Water (2) Mixed Solvent Media. J. Chem. Eng. Data 2011, 56, 3400–3405. [Google Scholar] [CrossRef]
- Huang, J.B.; Mao, M.; Zhu, B.Y. The surface physico-chemical properties of surfactants in ethanol-water mixtures. Coll. Surf. A 1999, 155, 339–348. [Google Scholar] [CrossRef]
- Shirzad, S.; Sadeghi, R. Micellization properties and related thermodynamic parameters of aqueous sodium dodecyl sulfate and sodium dodecyl sulfonate solutions in the presence of 1-propanol. Fluid Phase Equilib. 2014, 377, 1–8. [Google Scholar] [CrossRef]
- Zana, R. Aqueous Surfactant-Alcohol Systems—A Review. Adv. Coll. Interface 1995, 57, 1–64. [Google Scholar] [CrossRef]
- Janczuk, B.; Zdziennicka, A.; Wojcik, W. Adsorption of sodium dodecyl sulphate and propanol mixtures at aqueous solution-air interface. Coll. Surf. A 2004, 244, 1–7. [Google Scholar] [CrossRef]
- Magnaudet, J.; Eames, I. The motion of high-Reynolds-mumber bubbles in inhomogeneous flows. Annu. Rev. Fluid Mech. 2000, 32, 659–708. [Google Scholar] [CrossRef]
- Kulkarni, A.A.; Joshi, J.B. Bubble formation and bubble rise velocity in gas-liquid systems: A review. Ind. Eng. Chem. Res. 2005, 44, 5873–5931. [Google Scholar] [CrossRef]
- Moore, D.W. The Rise of a Gas Bubble in a Viscous Liquid. J. Fluid Mech. 1959, 6, 113–130. [Google Scholar] [CrossRef]
- Moore, D.W. Velocity of Rise of Distorted Gas Bubbles in a Liquid of Small Viscosity. J. Fluid Mech. 1965, 23, 749–766. [Google Scholar] [CrossRef]
- Moore, D.W. The Boundary Layer on a Spherical Gas Bubble. J. Fluid Mech. 1963, 16, 161–176. [Google Scholar] [CrossRef]
- Mei, R.W.; Adrian, R.J. Flow Past a Sphere with an Oscillation in the Free-Stream Velocity and Unsteady Drag at Finite Reynolds-Number. J. Fluid Mech. 1992, 237, 323–341. [Google Scholar] [CrossRef]
- Cuenot, B.; Magnaudet, J.; Spennato, B. The effects of slightly soluble surfactants on the flow around a spherical bubble. J. Fluid Mech. 1997, 339, 25–53. [Google Scholar] [CrossRef]
- Schiller, L.; Naumann, A. A drag coefficient correlation. Z. Ver. Deutsch. Ing. 1935, 77, 318–320. [Google Scholar]
- Hubicka, M.; Basarova, P.; Vejrazka, J. Collision of a small rising bubble with a large falling particle. Int. J. Min. Process. 2013, 121, 21–30. [Google Scholar] [CrossRef]
- Turton, R.; Levenspiel, O. A Short Note on the Drag Correlation for Spheres. Powder Technol. 1986, 47, 83–86. [Google Scholar] [CrossRef]
- Basarova, P.; Vachova, T.; Bartovska, L. Atypical wetting behaviour of alcohol-water mixtures on hydrophobic surfaces. Colloid Surf. A 2016, 489, 200–206. [Google Scholar] [CrossRef]
- Sung, J.H.; Park, K.; Kim, D. Surfaces of alcohol-water mixtures studied by sum-frequency generation vibrational spectroscopy. J. Phys. Chem. B 2005, 109, 18507–18514. [Google Scholar] [CrossRef]
- Nagasawa, Y.; Nakagawa, Y.; Nagafuji, A.; Okada, T.; Miyasaka, H. The microscopic viscosity of water-alcohol binary solvents studied by ultrafast spectroscopy utilizing diffusive phenyl ring rotation of malachite green as a probe. J. Mol. Struct. 2005, 735, 217–223. [Google Scholar] [CrossRef]
- Rosen, M.J. Surfactants and Interfacial Phenomena; John Wiley & Sons: Hoboken, NJ, USA, 2004. [Google Scholar] [CrossRef]
- Basarova, P.; Suchanova, H.; Souskova, K.; Vachova, T. Bubble adhesion on hydrophobic surfaces in solutions of pure and technical grade ionic surfactants. Colloid Surf. A 2017, 522, 485–493. [Google Scholar] [CrossRef]
- Mysels, K.J. Surface-Tension of Solutions of Pure Sodium Dodecyl-Sulfate. Langmuir 1986, 2, 423–428. [Google Scholar] [CrossRef]
- Zdziennicka, A.; Janczuk, B.; Wojcik, W. Adsorption of mixtures of sodium dodecyl sulphate and propanol at water-air and polytetrafluoroethylene-water interfaces. Colloid Surf. A 2004, 249, 73–77. [Google Scholar] [CrossRef]
- Kovtun, A.I.; Khil’ko, S.L.; Zholob, S.A.; Rybachenko, V.I. Effect of lower alcohols on adsorption characteristics of sodium dodecyl sulfate solutions at liquid-gas interfaces. Colloid J. 2010, 72, 389–395. [Google Scholar] [CrossRef]
- Manko, D.; Zdziennicka, A.; Szymczyk, K.; Janczuk, B. Influence of the propanol on the behaviour of binary mixture of nonionic surfactants at the water-air interface. J. Mol. Liq. 2014, 199, 196–201. [Google Scholar] [CrossRef]
- Pawliszak, P.; Ulaganathan, V.; Bradshaw-Hajek, B.H.; Manica, R.; Beattie, D.A.; Krasowska, M. Mobile or Immobile? Rise Velocity of Air Bubbles in High-Purity Water. J. Phys. Chem. C 2019, 123, 15131–15138. [Google Scholar] [CrossRef]
- Zhu, B.Y.; Rosen, M.J. Synergism in Binary-Mixtures of Surfactants.4. Effectiveness of Surface-Tension Reduction. J. Colloid Interf. Sci. 1984, 99, 435–442. [Google Scholar] [CrossRef]
- Dukhin, S.S.; Kovalchuk, V.I.; Gochev, G.G.; Lotfi, M.; Krzan, M.; Malysa, K.; Miller, R. Dynamics of Rear Stagnant Cap formation at the surface of spherical bubbles rising in surfactant solutions at large Reynolds numbers under conditions of small Marangoni number and slow sorption kinetics. Adv. Colloid Interface 2015, 222, 260–274. [Google Scholar] [CrossRef]
- Basařová, P.; Zawala, J.; Zedníková, M. Interactions between a Small Bubble and a Greater Solid Particle during the Flotation Process. Miner. Process. Extr. Metall. Rev. 2019, 1–17. [Google Scholar] [CrossRef]
- Zhang, X.R.; Manica, R.; Tang, Y.C.; Liu, Q.X.; Xu, Z.H. Bubbles with tunable mobility of surfaces in ethanol-NaCl aqueous solutions. J. Colloid Interf. Sci. 2019, 556, 345–351. [Google Scholar] [CrossRef]



| Molar Fraction xi | Mass Fraction wi | Temperature (°C) | Density (kg/m3) | Surface Tension (mN/m) | Dynamic Viscosity (mPa·s) |
|---|---|---|---|---|---|
| 0 | 0 | 24.0 | 997.3 | 72.1 | 0.911 |
| 0.001 | 0.0033 | 24.0 | 997.0 | 68.2 | 0.923 |
| 0.01 | 0.0326 | 24.0 | 992.6 | 50.4 | 1.045 |
| 0.10 | 0.2709 | 24.0 | 953.8 | 26.2 | 2.199 |
| 0.30 | 0.5890 | 24.0 | 887.5 | 25.4 | 2.810 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Basařová, P.; Kryvel, Y.; Crha, J. Bubble Rise Velocity and Surface Mobility in Aqueous Solutions of Sodium Dodecyl Sulphate and n-Propanol. Minerals 2019, 9, 743. https://doi.org/10.3390/min9120743
Basařová P, Kryvel Y, Crha J. Bubble Rise Velocity and Surface Mobility in Aqueous Solutions of Sodium Dodecyl Sulphate and n-Propanol. Minerals. 2019; 9(12):743. https://doi.org/10.3390/min9120743
Chicago/Turabian StyleBasařová, Pavlína, Yuliya Kryvel, and Jakub Crha. 2019. "Bubble Rise Velocity and Surface Mobility in Aqueous Solutions of Sodium Dodecyl Sulphate and n-Propanol" Minerals 9, no. 12: 743. https://doi.org/10.3390/min9120743
APA StyleBasařová, P., Kryvel, Y., & Crha, J. (2019). Bubble Rise Velocity and Surface Mobility in Aqueous Solutions of Sodium Dodecyl Sulphate and n-Propanol. Minerals, 9(12), 743. https://doi.org/10.3390/min9120743