Decision Theory versus Conventional Statistics for Personalized Therapy of Breast Cancer
Abstract
:1. Introduction
1.1. Biomarkers: A Cornerstone of Personalized Medicine for Breast Cancer
1.2. Basic Concepts of Decision Theory for Hormone Receptor Status Assessment
- The belief α(d), gives the probability (weight) that, upon measuring this particular value of d, the prediction ‘positive’ can be made based on the quality of measurement (classification ‘with full right’).
- The uncertainty θ(d), characterizing the probability (weight), that the prediction ‘positive’ could root in chance and not in quality of measurement. Belief and uncertainty taken together yield the total probability (termed ‘plausibility’) to obtain the prediction ‘positive’, given the measured value of d (α + θ = pl).
- Finally, a third number can be computed from belief and uncertainty, the probability β(d) for yielding the prediction ‘negative’ by quality of measurement, given d. We always have: α + θ + β = 1; hence, β can be computed from α and θ.
- For estrogen (ER)
- ○
- Receptor status predicted from expression of the receptor gene
- ○
- Receptor status predicted from expression of a co-gene
- ▪
- Combining above evidence by Dempster evidence combination rule ⊕D
- ○
- Receptor status predicted from IHC
- ▪
- Combining evidence from gene expression and IHC by Yager evidence combination rule ⊕Y
- For progesterone (PGR)
- ○
- Receptor status predicted from expression of the receptor gene
- ○
- Receptor status predicted from expression of a co-gene
- ▪
- Combining above evidence by Dempster evidence combination rule ⊕D
- ○
- Receptor status predicted from IHC
- ▪
- Combining evidence from gene expression and IHC by Yager evidence combination rule ⊕Y
- Hormone receptor status is finally obtained by combining the statuses of estrogen and progesterone using a multiplicative combination rule ⊗
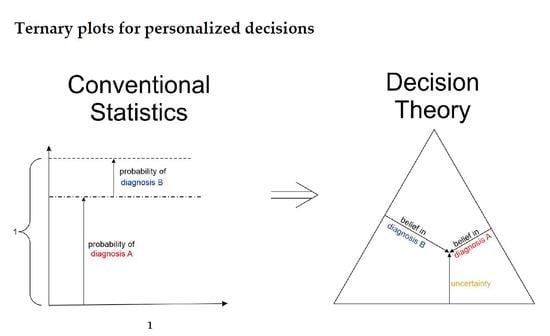
1.3. Ternary Plots: A Novel View on Evidence in Personalized Medicine
2. Materials and Methods
2.1. Preliminaries on the Structure of the Methods’ Section
2.2. Estrogen Receptor Gene Sub-Model
2.2.1. Logistic Regression as Prerequisite
2.2.2. Evidence of Receptor Status Based on Expression of Receptor Gene
- : the belief (sometimes also called ‘degree of belief’ or ‘credibility’ [74]) for receptor status being positive on good grounds or by quality of the measuring method that has yielded xExpr;
- βExpr: the belief (probability) for receptor status being non-positive (i.e., negative) on good grounds or by quality of the measuring method;
- θExpr is a third quantity considered: the probability that the receptor status is uncertain.
2.2.3. Combining Evidence from Receptor Gene Expression and IHC
2.2.4. Ternary Plots of Evidence for Personalized Medicine: A Primer
- Parallel lines at right angles with one axis represent constant values for the respective variable (as with ordinary right-angle axes). In particular, the line crossing the α–axis at α = 0.5 (dotted red) discriminates points with α ≤ 0.5 (left upper) from those with α > 0.5 (towards lower right corner), and hence represents a decision border; points right of this border are predicted ‘positive’, since their evidence for positive is greater than for all other options (‘negative’ and ‘uncertain’) taken together.
- Decision borders segregate subsets of samples. For example, all samples within the triangle in the lower right of α = 0.5 (shaded light red) comprise samples predicted positive. Similarly, the subsets of negative and uncertain samples may be defined, see Figure 4b.
- In each corner one piece of evidence totally dominates, assuming a value of unity (α = 1: ‘surely positive’; β = 1: ‘surely negative’ and θ = 1: ‘totally uncertain’).
- Conversely, the footing point of each axis (e.g., α = 0) means that there is no indication whatsoever for the prediction at opposing corner. For example, α = 0 along the left side of the triangle, means that there is no indication whatsoever for a ‘positive’ prediction. All evidence is shared between ‘negative’ and ‘uncertain’ (β and θ). In this case β + θ = 1.
- A special role is played by the triangle’s bottom edge, running from β = 1 (left) towards α = 1 (right): for each sample along this line uncertainty θ equals zero, and all evidence is shared between belief in positive (α) and belief in negative (β), e.g., α = 0.6 and β = 0.4, while θ = 0. One may legitimately ask: “Does this mean that the prediction was made for sure?”. Since α > 0.5 and dominates both other options, we consider this prediction clearly positive. However, α = 0.6 is no more than a probability and not that much larger than the probability of the opposite outcome, β = 0.4. In reality, the outcome may well result in a negative prediction. If θ = 0, evidence masses revert back to ordinary probabilities: p+ = 0.6 for positive and hence p− = 0.4 for negative, without indicating any uncertainty about the estimates of these two numbers. Thus, for θ = 0, decision theory’s evidence coincides with ordinary probabilities. In DST terminology the evidence is said to turn ‘Bayesian’ [74].
- In general, for θ > 0, decision theory not only gives estimates for probabilities (α, β) but additionally indicates the uncertainty of those (θ). It hence offers a wider scope of evidence, valuable in particular for personalized medicine.
- The location of the point indicates the prediction according to DST shown by the respective area: red triangular area for positive (+), blue for negative (-) and the white, kite-shaped area for inconclusive (inc).
- At the same time, coloring of points indicates prediction according to ODDS. For most samples, both predictions match. For some samples however, they differ, thus perfectly outlining the contrast between the two prediction methods.
2.3. Full Model: Evidence, Based on IHC, Genes, Co-Genes
2.3.1. Progesterone Evidence
2.3.2. Combining Evidence Form Genes and Co-Genes
2.3.3. Combining Evidence from Gene Expression and IHC
2.3.4. Combining Estrogen and Progesterone Receptor Status
3. Results
3.1. Contrasting Predictions by ODDS versus DST
- In the left panels, samples are geometrically located according to ODDS scores, but color-coded according to DST prediction.
- Decision borders in ODDS can be directly displayed in an orthogonal, 2-dimensional plot of ‘scores’, see Figure 6, left panels. Decision borders are defined by specific values for each receptor score (ER score, PGR score), see our previous paper [37], and, hence, appear as vertical lines for estrogen and as horizontal lines for progesterone, respectively. The rectangular region (in faint blue) denotes receptor status predicted definitely negative, the L-shaped stripe (no color) denotes inconclusive status, and the L-shaped stripe (in faint red) definitely positive predictions.
- ODDS scores incorporate IHC evidence in an additive fashion. Each of the nine possible IHC statuses (+ +, − −, + −, − +, + 0, 0 +, − 0, 0 −, 0 0) merely differ in shifts along the respective ODDS coordinate (ER score, PGR score). ODDS decision borders are, hence, valid for any combination of IHC statuses.
- In the right panels, samples are geometrically located according to DST evidence, but color-coded according to ODDS.
- Decision borders in DST are most appropriately displayed in ternary plots of evidence, see Figure 6, right panels. Decision borders run along evidence α = 0.5 and β = 0.5, respectively, which appear as straight lines in a ternary plot. DST evidence also incorporates IHC information, and decision lines, hence, also represent unique borders in the ternary plot, valid for any combination of IHC statuses (+ +, − −, + −, − +, + 0, 0 +, etc.).
- In the ternary plot, DST evidence for subsets of patient samples appear in polygonal areas. In fact, these areas root in respective combinations of IHC statuses for estrogen and progesterone (+ +, − −, + −, etc.), as will be scrutinized in the appendix, for those interested in mathematical details. Indeed, these polygonal areas are generalizations of those simple straight lines already seen with single gene expression data (Figure 4). Since each receptor may assume three values (+, −, 0), there are 32 = 9 possible IHC status combinations for two receptors. Some IHC statuses give rise to very distinct arrangements of samples, such as ‘lines’. Other IHC combinations give rise to more polygonal-shaped areas. Details will be discussed below. Data samples along these lines or polygons are seen to cross DST decision borders (dashed lines at α = 0.5 and β = 0.5, respectively). For example, if such a subset of samples crosses from inconclusive to decided, this indicates that IHC on its own was inconclusive, but adding evidence from (increasing) gene expression finally rendered a decision:
- ○
- A stripe of red points originates within the DST-inconclusive, kite-shaped area and protrudes into the positive triangle.
- ○
- The stripe of blue points originates in the DST-inconclusive, kite-shaped area and protrudes into the negative triangle.
3.2. Clinical Relevance of DST versus ODDS
- For 10 patients, DST predicted a positive receptor status, whereas ODDS had predicted ‘undecided’. Based on the additional information provided by DST, these patients may, upon careful reassessment, be candidates for milder therapies, possibly without chemotherapy (chemo). We, therefore, labelled this group with ‘adding information’ in Figure 6, panel (c).
- For 40 patients, DST predicted ‘undecided’, whereas ODDS had predicted ‘positive’. ‘Undecided’ severely questions abstaining from chemo and calls for a re-assessment at least. We, therefore, labelled this group with ‘increasing safety’ in Figure 6, panel (d).
3.3. Specific Differences in Prediction between ODDS and DST
- Within the plane of ODDS scores (left panel), the L-shaped area (colored faint red) denotes samples definitely predicted positive by ODDS (according to location). However, some of them are inconclusive according to DST (colored beige); in fact, 40 DST-inconclusive samples invade the positive, and the other 45, the negative domain of ODDS scores, see Table 1.
- Conversely, the uncolored L-shaped area accommodates samples predicted inconclusive according to ODDS (according to location). However, 10 are colored red, i.e., according to DST, decided positive. In fact, these samples, definitely predicted positive by DST, invade the inconclusive region of ODDS scores and are labelled ‘adding information’, see Figure 6, panel (c) and Table 1.
- Within the ternary plot of DST evidence (right panel), the triangular shaped areas denote samples predicted negative (faint blue) and positive (faint red), respectively, according to DST (by location). However, some samples are color-coded beige, i.e., they were rendered inconclusive by ODDS. Note that the very same samples appear in dual roles along ODDS scores and ternary evidence, respectively (left and right panel).
- Conversely, the uncolored kite-shaped area denotes samples predicted inconclusive according to DST (by location). However, some of them are color-coded red or blue, i.e., definitely predicted as positive or negative according to ODDS. In fact, 40 samples definitely classified positive through ODDS intrude into the ‘inconclusive’ region of DST and have been labelled as ‘increasing safety’, see panel (d). Another 45 definitely predicted negative through ODDS intrude into the ‘inconclusive’ region of DST.
4. Discussion
4.1. Advantages of Evidence Compared to Probabilities in Conventional Statistics
- Obtain DST evidence from gene expression.
- Obtain DST evidence from IHC.
- Fuse both items of evidence above, via the Yager evidence combination rule [78].
- Display results in a ‘ternary’ plot, a genuine format for presenting evidence.
- Show subgroups of patients with given IHC status, giving rise to specific patterns of samples in evidence space.
4.2. How Uncertainty May Help Increase Correctness (Precision)
4.3. Extensions of Decision Rules
4.4. Modelling Sharp and Soft Clinical Decisions
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
Appendix A.1. Download and Cleansing of Data
- Only tumor samples were considered, controls excluded;
- Only tissue samples were considered, cell lines excluded;
- Replicates were removed;
- All samples were pairwise checked for being duplicates. CEL files with equal medical data (expression, clinical) may differ, just in format or container packing. Hence, actual expression values needed to be compared to safely locate duplicates;
- If duplicates in expression data were found to differ in metadata, these were curated manually;
- Some GSE studies have been ‘enriched’ with samples from other (previous) GSE studies. Such samples become duplicates if both of these studies were evaluated in combination. We always left such samples with their original study and removed its duplicate from the later GSE study;
- We detected damaged samples by RMAexpress [93] and removed them;
Appendix A.2. Selecting HER2 Negative Patients
| N | ||||
|---|---|---|---|---|
| Study | City | All | ERIHC | PGRIHC |
| GSE5460 | Boston | 17 | 17 | 0 |
| GSE6532 | Toronto | 78 | 78 | 77 |
| GSE12276 | Rotterdam | 118 | 0 | 0 |
| GSE16391 | Toronto | 50 | 50 | 50 |
| GSE16446 | Toronto | 84 | 84 | 0 |
| GSE18728 | Seattle | 15 | 15 | 14 |
| GSE18864 | Lyngby | 60 | 60 | 60 |
| GSE19615 | Manhattan | 79 | 79 | 79 |
| GSE20685 | Taipei | 163 | 0 | 0 |
| GSE20711 | Toronto | 52 | 52 | 0 |
| GSE22035 | SAINT-CLOUD | 27 | 27 | 0 |
| GSE23177 | Leuven | 80 | 80 | 0 |
| GSE26639 | Paris Cedex 05 | 144 | 144 | 142 |
| GSE27120 | Brussels | 26 | 26 | 26 |
| GSE29431 | Barcelona | 23 | 23 | 23 |
| GSE31448 | Marseille | 286 | 286 | 271 |
| GSE36771 | Auckland | 86 | 86 | 85 |
| GSE42568 | Dublin | 65 | 63 | 0 |
| GSE43358 | Brussels | 43 | 43 | 43 |
| GSE43365 | Boston | 98 | 98 | 98 |
| GSE46222 | Washington | 26 | 26 | 0 |
| GSE47389 | Rotterdam | 47 | 47 | 47 |
| GSE48390 | New Taipei City | 34 | 34 | 0 |
| GSE48905 | Hørsholm | 20 | 20 | 0 |
| GSE50567 | Gliwice | 25 | 25 | 0 |
| GSE58792 | New York | 33 | 33 | 0 |
| GSE58812 | Saint Herblain | 107 | 107 | 107 |
| GSE61304 | Singapore | 41 | 38 | 33 |
| GSE65194 | PARIS | 70 | 67 | 41 |
| GSE71258 | Missouri | 94 | 77 | 77 |
| GSE76124 | Houston | 198 | 198 | 198 |
| GSE76274 | Houston | 44 | 44 | 44 |
| GSE87007 | Brussels | 24 | 24 | 24 |
| GSE88770 | Brussels | 108 | 108 | 107 |
| GSE95700 | Taipei City | 54 | 54 | 54 |
| ∑ | 2519 | 2213 | 1700 | |
Appendix A.3. Selecting Genes and Probe Sets for Estrogen and Progesterone Receptors
| Logistic Regression Parameters | Logistic Regression Quality | Upper Limits for Beliefs | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Probe Set | Deviance of Fit | Number of Samples | |||||||
| estrogen | gene | ESR1 | 205225_at | 9.905 | −1.061 | 1086.6 | 2213 | 0.814 | 0.887 |
| co- gene | AGR3 | 228241_at | 5.582 | −0.710 | 1253.1 | 0.794 | 0.840 | ||
| progesterone | gene | PGR | 208305_at | 7.449 | −0.983 | 1107.4 | 1700 | 0.753 | 0.702 |
| co- gene | ESR1 | 205225_at | 8.617 | −0.834 | 1249.8 | 0.618 | 0.817 | ||
| Logistic Regression Parameters | Logistic Regression Quality | ||||||
|---|---|---|---|---|---|---|---|
| Probe Set | Deviance of Fit | Number of Samples | |||||
| HER2 | gene | ERBB2 | 216836_s_at | 15.963 | −1.408 | 1421.2 | 2430 |
| co-gene | PGAP3 | 221811_at | 17.756 | −2.168 | 1330.6 | ||

Appendix A.4. Tailoring Beliefs in Receptor Gene Expression to a Given Accuracy of IHC
Appendix A.5. Formulating IHC Data in Terms of Evidence
- Due to the positive IHC measurement, there is no evidence at all for the status being (truly) negative due to quality of the method, hence .
- Being measured as true positive by chance or as false positive by error represents all measurements not being true by quality of the method. Together they make up 30%, represented by . We assume that these split in equal parts into 15% true positive by chance and 15% false positive by error.
- Hence, cases being true by quality make up the remaining 70%, represented by .
- Since all items add up to 1 (Equation (2)), we obtain , and the whole evidence after a positive IHC result is (, , ).

Appendix A.6. Ternary Plots Reflect Subgroups within Patient Cohort
- Evidence for patients is not distributed evenly all over the ‘triangle plain of evidence’, but samples are grouped in ‘traces’, which deserves explanation: first, we note that exactly three lines appear and each sample belongs to one of these lines; no sample is found apart. The fact that we deal with three possible states of IHC values (+, −, inc) already points towards a possible reason, and this is in fact true: it is varying IHC statuses, which give rise to these lines. Suppose that, for a given IHC status, e.g., positive, we consider different values of gene expression, xExpr. When computing corresponding evidence, , these will appear along a straight line. This is visually obvious but can, in fact, be formally proven mathematically, resorting to Equations (1), (4) and (6). Hence, each of the specific lines may be labeled, accordingly (, and ), see Figure 4a.
- Note also that the red line of samples starts near the corner α = 1, but not exactly at the corner: even a positive IHC and large gene expression cannot guarantee a positive prediction—some small uncertainty (θ) remains. At the same time, for such a sample, there is no evidence whatsoever for a negative status. Hence β = 0, and the line starts at the ternary plot’s side representing β = 0. Such a sample represents the total opposite to the lower left corner—where β = 1 (surely negative).
- After originating close to the lower right corner of (marked with α = 1) the line for (red), proceeds across the sub-area indicating receptor positive (shaded red). These samples have status (all dots, no circles), being confirmed by gene expression, ending up as positive predictions. After crossing the decision border at α = 0.5, this line still represents samples with , which has obviously been questioned by gene expression; hence, prediction was rendered ‘inconclusive’ according to DST (samples lie within the kite-shaped area). Coloring these samples, according to ODDS, most vividly reveals differences in prediction: although located within the DST-inconclusive region, ODDS predicts some of these samples as positive, the majority as inconclusive (i.e., agrees with DST), but a few as negative (see the blue dots towards the end of the line in the upper left).
- Note that lines for and never protrude into the opposing definite areas, for the following reason: given , gene expression can by no means reverse the prediction to surely negative. At the most, it may downgrade it to inconclusive. The same is true for . The white, kite-shaped area segregates the areas of positive and negative predictions, which is reasonable.
- Only at one single point, two strongly opposing items of evidence might, in principle, become close to one another (at the point α = β = 0.5, along the baseline of the ternary plot, see the tutorial Section 2.2.4 for further discussion). As a matter of fact, such samples do not occur in reality (in our cohort), and both lines meet farther outside, within the inconclusive region. In other words, if evidence incorporates contradiction, DST renders them inconclusive—as a precaution.
- Finally, the line for crosses the whole decision triangle, from surely positive (right side) through the inconclusive region (mid), towards surely negative (left side). Since no IHC status is available for these samples (shown as circles), gene expression is free to render this ample range of predictions.
Appendix A.7. Evidence Patterns for Subsets of Patients
- Since an MPD represents a maximum area, no sample of the same color appears outside, e.g., no blue sample (predicted negative by DST) may lie outside the blue MPD in the left panel of Figure A3.
- No blue sample (predicted negative by ODDS) may lie outside the blue MPD in the right panel of Figure A3.
- While predictions coded in color transgress decision borders according to location, they never leave the maximum accessible prediction domain of their own prediction method.
- Samples of real patients were never seen to yield contradicting predictions (e.g., negative by DSST and positive by ODDS), but MPDs well intrude into contradicting domains. For example, the negative MPD of DST (outlined blue) not only reaches into the inconclusive region, but well overlaps, even with the positive area of ODDS (Figure A3, left column, row 1). A second example is the positive MPD of ODDS (outlined red), penetrating into the decisively negative domain of DST (Figure A3, right column, row 3).
- Note that these ‘contradicting’ overlaps are rooted in extreme expression values, occurring in generated samples only, but have never been seen in our real data. Thus, these potential areas of contradiction between ODDS and DST remain a theoretical possibility to be considered, which does not infringe, however, application of these methods to data of real studies.
- Note that the dots (evidence) of these 10,000 simulated samples are not evenly distributed over the MPD. This is similar to the evidence of real samples; these also appear in fairly restricted zones, well within the respective MPD. One could generate 2-dimensional histograms, showing the density of these simulated samples.










References
- Toss, A.; Cristofanilli, M. Molecular characterization and targeted therapeutic approaches in breast cancer. Breast Cancer Res. 2015, 17, 60. [Google Scholar] [CrossRef]
- Dowsett, M.; Sestak, I.; Lopez-Knowles, E.; Sidhu, K.; Dunbier, A.K.; Cowens, J.W.; Ferree, S.; Storhoff, J.; Schaper, C.; Cuzick, J. Comparison of PAM50 risk of recurrence score with oncotype DX and IHC4 for predicting risk of distant recurrence after endocrine therapy. J. Clin. Oncol. 2013, 31, 2783–2790. [Google Scholar] [CrossRef]
- Prat, A.; Ellis, M.J.; Perou, C.M. Practical implications of gene-expression-based assays for breast oncologists. Nat. Rev. Clin. Oncol. 2011, 9, 48–57. [Google Scholar] [CrossRef] [Green Version]
- Huang, C.C.; Tu, S.H.; Lien, H.H.; Jeng, J.Y.; Huang, C.S.; Huang, C.J.; Lai, L.C.; Chuang, E.Y. Concurrent Gene Signatures for Han Chinese Breast Cancers. PLoS ONE 2013, 8, e76421. [Google Scholar] [CrossRef] [Green Version]
- Desmedt, C.; Haibe-Kains, B.; Wirapati, P.; Buyse, M.; Larsimont, D.; Bontempi, G.; Delorenzi, M.; Piccart, M.; Sotiriou, C. Biological processes associated with breast cancer clinical outcome depend on the molecular subtypes. Clin. Cancer Res. 2008, 14, 5158–5165. [Google Scholar] [CrossRef] [Green Version]
- Kao, K.J.; Chang, K.M.; Hsu, H.C.; Huang, A.T. Correlation of microarray-based breast cancer molecular subtypes and clinical outcomes: Implications for treatment optimization. BMC Cancer 2011, 11, 143. [Google Scholar] [CrossRef] [Green Version]
- Jezequel, P.; Loussouarn, D.; Guerin-Charbonnel, C.; Campion, L.; Vanier, A.; Gouraud, W.; Lasla, H.; Guette, C.; Valo, I.; Verriele, V.; et al. Gene-expression molecular subtyping of triple-negative breast cancer tumours: Importance of immune response. Breast Cancer Res. 2015, 17, 43. [Google Scholar] [CrossRef] [Green Version]
- Burstein, M.D.; Tsimelzon, A.; Poage, G.M.; Covington, K.R.; Contreras, A.; Fuqua, S.A.; Savage, M.I.; Osborne, C.K.; Hilsenbeck, S.G.; Chang, J.C.; et al. Comprehensive Genomic Analysis Identifies Novel Subtypes and Targets of Triple-negative Breast Cancer. Clin. Cancer Res. 2015, 21, 1688–1698. [Google Scholar] [CrossRef] [Green Version]
- Desmedt, C.; Giobbie-Hurder, A.; Neven, P.; Paridaens, R.; Christiaens, M.R.; Smeets, A.; Lallemand, F.; Haibe-Kains, B.; Viale, G.; Gelber, R.D.; et al. The Gene expression Grade Index: A potential predictor of relapse for endocrine-treated breast cancer patients in the BIG 1 Çô98 trial. BMC Med. Genom. 2009, 2, 40. [Google Scholar] [CrossRef] [Green Version]
- Wu, G.; Stein, L. A network module-based method for identifying cancer prognostic signatures. Genome Biol. 2012, 13, R112. [Google Scholar] [CrossRef] [Green Version]
- Liu, R.; Guo, C.X.; Zhou, H.H. Network-based approach to identify prognostic biomarkers for estrogen receptor–positive breast cancer treatment with tamoxifen. Cancer Biol. Ther. 2015, 16, 317–324. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Korde, L.A.; Lusa, L.; McShane, L.; Lebowitz, P.F.; Lukes, L.; Camphausen, K.; Parker, J.S.; Swain, S.M.; Hunter, K.; Zujewski, J.A. Gene expression pathway analysis to predict response to neoadjuvant docetaxel and capecitabine for breast cancer. Breast Cancer Res. Treat. 2010, 119, 685–699. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Clarke, C.; Madden, S.F.; Doolan, P.; Aherne, S.T.; Joyce, H.; O’Driscoll, L.; Gallagher, W.M.; Hennessy, B.T.; Moriarty, M.; Crown, J.; et al. Correlating transcriptional networks to breast cancer survival: A large-scale coexpression analysis. Carcinogenesis 2013, 34, 2300–2308. [Google Scholar] [CrossRef] [PubMed]
- Aswad, L.; Yenamandra, S.P.; Ow, G.S.; Grinchuk, O.; Ivshina, A.V.; Kuznetsov, V.A. Genome and transcriptome delineation of two major oncogenic pathways governing invasive ductal breast cancer development. Oncotarget 2015, 6, 36652–36674. [Google Scholar] [CrossRef] [Green Version]
- Filipits, M.; Rudas, M.; Jakesz, R.; Dubsky, P.; Fitzal, F.; Singer, C.F.; Dietze, O.; Greil, R.; Jelen, A.; Sevelda, P.; et al. A new molecular predictor of distant recurrence in ER-positive, HER2-negative breast cancer adds independent information to conventional clinical risk factors. Clin. Cancer Res. 2011, 17, 6012–6020. [Google Scholar] [CrossRef] [Green Version]
- Zhao, X.; Rødland, E.A.; Sørlie, T.; Vollan, H.K.; Russnes, H.G.; Kristensen, V.N.; Lingjærde, O.C.; Børresen-Dale, A.-L. Systematic assessment of prognostic gene signatures for breast cancer shows distinct influence of time and ER status. BMC Cancer 2014, 14, 211. [Google Scholar] [CrossRef] [Green Version]
- Van’t Veer, L.J.; Dai, H.; van de Vijver, M.J.; He, Y.D.; Hart, A.A.; Mao, M.; Peterse, H.L.; van der Kooy, K.; Marton, M.J.; Witteveen, A.T. Gene expression profiling predicts clinical outcome of breast cancer. Nature 2002, 415, 530–536. [Google Scholar] [CrossRef] [Green Version]
- Van de Vijver, M.J.; He, Y.D.; van’t Veer, L.J.; Dai, H.; Hart, A.A.M.; Voskuil, D.W.; Schreiber, G.J.; Peterse, J.L.; Roberts, C.; Marton, M.J.; et al. A Gene-Expression Signature as a Predictor of Survival in Breast Cancer. N. Engl. J. Med. 2002, 347, 1999–2009. [Google Scholar] [CrossRef] [Green Version]
- Paik, S.; Shak, S.; Tang, G.; Kim, C.; Baker, J.; Cronin, M.; Baehner, F.L.; Walker, M.G.; Watson, D.; Park, T. A multigene assay to predict recurrence of tamoxifen-treated, node-negative breast cancer. N. Engl. J. Med. 2004, 351, 2817–2826. [Google Scholar] [CrossRef] [Green Version]
- Lu, X.; Lu, X.; Wang, Z.C.; Iglehart, J.D.; Zhang, X.; Richardson, A.L. Predicting features of breast cancer with gene expression patterns. Breast Cancer Res. Treat. 2008, 108, 191–201. [Google Scholar] [CrossRef]
- Budczies, J.; Weichert, W.; Noske, A.; Muller, B.M.; Weller, C.; Wittenberger, T.; Hofmann, H.P.; Dietel, M.; Denkert, C.; Gekeler, V. Genome-wide gene expression profiling of formalin-fixed paraffin-embedded breast cancer core biopsies using microarrays. J. Histochem. Cytochem. 2011, 59, 146–157. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lin, C.Y.; Ström, A.; Vega, V.B.; Li Kong, S.; Li Yeo, A.; Thomsen, J.S.; Chan, W.C.; Doray, B.; Bangarusamy, D.K.; Ramasamy, A.; et al. Discovery of estrogen receptor α target genes and response elements in breast tumor cells. Genome Biol. 2004, 5, R66. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Liu, M.C.; Pitcher, B.N.; Mardis, E.R.; Davies, S.R.; Friedman, P.N.; Snider, J.E.; Vickery, T.L.; Reed, J.P.; DeSchryver, K.; Singh, B.; et al. PAM50 gene signatures and breast cancer prognosis with adjuvant anthracycline- and taxane-based chemotherapy: Correlative analysis of C9741 (Alliance). NPJ Breast Cancer 2016, 2, 15023. [Google Scholar] [CrossRef] [PubMed]
- Prat, A.; Bianchini, G.; Thomas, M.; Belousov, A.; Cheang, M.C.; Koehler, A.; Gomez, P.; Semiglazov, V.; Eiermann, W.; Tjulandin, S.; et al. Research-based PAM50 subtype predictor identifies higher responses and improved survival outcomes in HER2-positive breast cancer in the NOAH study. Clin. Cancer Res. 2014, 20, 511–521. [Google Scholar] [CrossRef] [Green Version]
- Wishart, G.C.; Azzato, E.M.; Greenberg, D.C.; Rashbass, J.; Kearins, O.; Lawrence, G.; Caldas, C.; Pharoah, P.D.P. PREDICT: A new UK prognostic model that predicts survival following surgery for invasive breast cancer. Breast Cancer Res. 2010, 12, R1. [Google Scholar] [CrossRef] [Green Version]
- Metzger-Filho, O.; Catteau, A.; Michiels, S.; Buyse, M.; Ignatiadis, M.; Saini, K.S.; de Azambuja, E.; Fasolo, V.; Naji, S.; Canon, J.L.; et al. Genomic Grade Index (GGI): Feasibility in Routine Practice and Impact on Treatment Decisions in Early Breast Cancer. PLoS ONE 2013, 8, e66848. [Google Scholar] [CrossRef]
- Rhodes, A.; Jasani, B.; Balaton, A.; Miller, K. Immunohistochemical demonstration of oestrogen and progesterone receptors: Correlation of standards achieved on in house tumours with that achieved on external quality assessment material in over 150 laboratories from 26 countries. J. Clin. Pathol. 2000, 53, 292–301. [Google Scholar] [CrossRef] [Green Version]
- Wolff, A.C.; Hammond, M.E.; Schwartz, J.N.; Hagerty, K.L.; Allred, D.C.; Cote, R.J.; Dowsett, M.; Fitzgibbons, P.L.; Hanna, W.M.; Langer, A.; et al. American Society of Clinical Oncology/College of American Pathologists Guideline Recommendations for Human Epidermal Growth Factor Receptor 2 Testing in Breast Cancer. J. Clin. Oncol. 2006, 25, 118–145. [Google Scholar]
- Sparano, J.A.; Muss, H. Learning from big data: Are we undertreating older women with high-risk breast cancer? NPJ Breast Cancer 2016, 2, 16019. [Google Scholar] [CrossRef] [Green Version]
- Harris, L.N.; Ismaila, N.; McShane, L.M.; Andre, F.; Collyar, D.E.; Gonzalez-Angulo, A.M.; Hammond, E.H.; Kuderer, N.M.; Liu, M.C.; Mennel, R.G.; et al. Use of Biomarkers to Guide Decisions on Adjuvant Systemic Therapy for Women with Early-Stage Invasive Breast Cancer: American Society of Clinical Oncology Clinical Practice Guideline. J. Clin. Oncol. 2016, 34, 1134–1150. [Google Scholar] [CrossRef] [Green Version]
- Singer, C.F.; Tan, Y.Y.; Fitzal, F.; Steger, G.G.; Egle, D.; Reiner, A.; Rudas, M.; Moinfar, F.; Gruber, C.; Petru, E.; et al. Pathological Complete Response to Neoadjuvant Trastuzumab Is Dependent on HER2/CEP17 Ratio in HER2-Amplified Early Breast Cancer. Clin. Cancer Res. 2017, 23, 3676–3683. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Harbeck, N.; Gnant, M. Breast cancer. Lancet 2016, 389, 1134–1150. [Google Scholar] [CrossRef]
- Wirapati, P.; Sotiriou, C.; Kunkel, S.; Farmer, P.; Pradervand, S.; Haibe-Kains, B.; Desmedt, C.; Ignatiadis, M.; Sengstag, T.; Schütz, F.; et al. Meta-analysis of gene expression profiles in breast cancer: Toward a unified understanding of breast cancer subtyping and prognosis signatures. Breast Cancer Res. 2008, 10, R65. [Google Scholar] [CrossRef] [PubMed]
- Hudis, C.A.; Barlow, W.E.; Costantino, J.P.; Gray, R.J.; Pritchard, K.I.; Chapman, J.A.W.; Sparano, J.A.; Hunsberger, S.; Enos, R.A.; Gelber, R.D.; et al. Proposal for standardized definitions for efficacy end points in adjuvant breast cancer trials: The STEEP system. J. Clin. Oncol. 2007, 25, 2127–2132. [Google Scholar] [CrossRef]
- Regan, M.M.; Viale, G.; Mastropasqua, M.G.; Maiorano, E.; Golouh, R.; Carbone, A.; Brown, B.; Suurküla, M.; Langman, G.; Mazzucchelli, L.; et al. Re-evaluating Adjuvant Breast Cancer Trials: Assessing Hormone Receptor Status by Immunohistochemical Versus Extraction Assays. J. Natl. Cancer Inst. 2006, 98, 1571–1581. [Google Scholar] [CrossRef] [Green Version]
- Kaufmann, M.; Pusztai, L.; Members, B.E.P. Use of standard markers and incorporation of molecular markers into breast cancer therapy: Consensus recommendations from an International Expert Panel. Cancer 2011, 117, 1575–1582. [Google Scholar] [CrossRef]
- Kenn, M.; Cacsire Castillo-Tong, D.; Singer, C.F.; Karch, R.; Cibena, M.; Koelbl, H.; Schreiner, W. Decision theory for precision therapy of breast cancer. Sci. Rep. 2021, 11, 4233. [Google Scholar] [CrossRef]
- Bartlett, J.M.; Campbell, F.M.; Ibrahim, M.; O’Grady, A.; Kay, E.; Faulkes, C.; Collins, N.; Starczynski, J.; Morgan, J.M.; Jasani, B.; et al. A UK NEQAS ISH multicenter ring study using the Ventana HER2 dual-color ISH assay. Am. J. Clin. Pathol. 2011, 135, 157–162. [Google Scholar] [CrossRef] [Green Version]
- Lee, M.; Lee, C.S.; Tan, P.H. Hormone receptor expression in breast cancer: Postanalytical issues. J. Clin. Pathol. 2013, 66, 478–484. [Google Scholar] [CrossRef]
- Hammond, M.E.; Hayes, D.F.; Wolff, A.C.; Mangu, P.B.; Temin, S. American Society of Clinical Oncology/College of American Pathologists Guideline Recommendations for Immunohistochemical Testing of Estrogen and Progesterone Receptors in Breast Cancer. J. Oncol. Pract. 2010, 6, 195–197. [Google Scholar] [CrossRef] [Green Version]
- Wells, C.A.; Sloane, J.P.; Coleman, D.; Munt, C.; Amendoeira, I.; Apostolikas, N.; Bellocq, J.P.; Bianchi, S.; Boecker, W.; Bussolati, G.; et al. Consistency of staining and reporting of oestrogen receptor immunocytochemistry within the European Union-An inter-laboratory study. Virchows Arch. 2004, 445, 119–128. [Google Scholar] [CrossRef] [PubMed]
- Laas, E.; Mallon, P.; Duhoux, F.P.; Hamidouche, A.; Rouzier, R.; Reyal, F. Low concordance between gene expression signatures in ER positive HER2 negative breast carcinoma could impair their clinical application. PLoS ONE 2016, 11, e0148957. [Google Scholar] [CrossRef] [PubMed]
- Rakha, E.A.; Pinder, S.E.; Bartlett, J.M.; Ibrahim, M.; Starczynski, J.; Carder, P.J.; Provenzano, E.; Hanby, A.; Hales, S.; Lee, A.H.; et al. Updated UK Recommendations for HER2 assessment in breast cancer. J. Clin. Pathol. 2015, 68, 93–99. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Allred, D.C.; Carlson, R.W.; Berry, D.A.; Burstein, H.J.; Edge, S.B.; Goldstein, L.J.; Gown, A.; Hammond, M.E.; Iglehart, J.D.; Moench, S.; et al. NCCN Task Force Report: Estrogen Receptor and Progesterone Receptor Testing in Breast Cancer by Immunohistochemistry. J. Natl. Compr. Cancer Netw. 2009, 7 (Suppl. 6), S1–S21. [Google Scholar] [CrossRef] [PubMed]
- Li, Q.; Eklund, A.C.; Juul, N.; Haibe-Kains, B.; Workman, C.T.; Richardson, A.L.; Szallasi, Z.; Swanton, C. Minimising immunohistochemical false negative ER classification using a complementary 23 gene expression signature of ER status. PLoS ONE 2010, 5, e15031. [Google Scholar] [CrossRef] [Green Version]
- Bergqvist, J.; Ohd, J.F.; Smeds, J.; Klaar, S.; Isola, J.; Nordgren, H.; Elmberger, G.P.; Hellborg, H.; Bjohle, J.; Borg, A.L.; et al. Quantitative real-time PCR analysis and microarray-based RNA expression of HER2 in relation to outcome. Ann. Oncol. 2007, 18, 845–850. [Google Scholar] [CrossRef]
- Chen, X.; Li, J.; Gray, W.H.; Lehmann, B.D.; Bauer, J.A.; Shyr, Y.; Pietenpol, J.A. TNBCtype: A subtyping tool for triple-negative breast cancer. Cancer Inform. 2012, 11, 147–156. [Google Scholar] [CrossRef]
- Gong, Y.; Yan, K.; Lin, F.; Anderson, K.; Sotiriou, C.; Andre, F.; Holmes, F.A.; Valero, V.; Booser, D.; Pippen, J.; et al. Determination of oestrogen-receptor status and ERBB2 status of breast carcinoma: A gene-expression profiling study. Lancet Oncol. 2007, 8, 203–211. [Google Scholar] [CrossRef]
- Lopez, F.J.; Cuadros, M.; Cano, C.; Concha, A.; Blanco, A. Biomedical application of fuzzy association rules for identifying breast cancer biomarkers. Med. Biol. Eng. Comput. 2012, 50, 981–990. [Google Scholar] [CrossRef]
- Owzar, K.; Barry, W.T.; Jung, S.H.; Sohn, I.; George, S.L. Statistical Challenges in Pre-Processing in Microarray Experiments in Cancer. Clin. Cancer Res. 2008, 14, 5959–5966. [Google Scholar] [CrossRef] [Green Version]
- Wu, Z. A Review of Statistical Methods for Preprocessing Oligonucleotide Microarrays. Stat. Methods Med. Res. 2009, 18, 533–541. [Google Scholar] [PubMed]
- Wu, Z.; Irizarry, R.A. Preprocessing of oligonucleotide array data. Nat. Biotechnol. 2004, 22, 656–658. [Google Scholar] [CrossRef] [PubMed]
- Wu, Z.; Irizarry, R.A.; Gentleman, R.; Martinez-Murillo, F.; Spencer, F. A Model-Based Background Adjustment for Oligonucleotide Expression Arrays. J. Am. Stat. Assoc. 2004, 99, 909–917. [Google Scholar] [CrossRef] [Green Version]
- Zhang, B.; Horvath, S. A general framework for weighted gene co-expression network analysis. Stat. Appl. Genet. Mol. Biol. 2005, 4, 17. [Google Scholar] [CrossRef] [PubMed]
- Ritchie, M.E.; Phipson, B.; Wu, D.; Hu, Y.; Law, C.W.; Shi, W.; Smyth, G.K. limma powers differential expression analyses for RNA-sequencing and microarray studies. Nucleic Acids Res. 2015, 43, e47. [Google Scholar] [CrossRef] [PubMed]
- Wu, Z.; Irizarry, R.A. A Statistical Framework for the Analysis of Microarray Probe-Level Data. Ann. Appl. Stat. 2007, 1, 333–357. [Google Scholar] [CrossRef]
- Bolstad, B.M.; Irizarry, R.A.; Astrand, M.; Speed, T.P. A comparison of normalization methods for high density oligonucleotide array data based on variance and bias. Bioinformatics 2003, 19, 185–193. [Google Scholar] [CrossRef] [Green Version]
- Kenn, M.; Cacsire Castillo-Tong, D.; Singer, C.F.; Cibena, M.; Kölbl, H.; Schreiner, W. Co-expressed genes enhance precision of receptor status identification in breast cancer patients. Breast Cancer Res. Treat. 2018, 172, 313–326. [Google Scholar] [CrossRef]
- Kenn, M.; Schlangen, K.; Cacsire Castillo-Tong, D.; Singer, C.F.; Cibena, M.; Koelbl, H.; Schreiner, W. Gene expression information improves reliability of receptor status in breast cancer patients. Oncotarget 2017, 8, 77341–77359. [Google Scholar] [CrossRef] [Green Version]
- Gordon, J.; Shortliffe, E.H. The Dempster-Shafer Theory of Evidence. In Rule-Based Expert Systems: The MYCIN Experiments of the Stanford Heuristic Programming Project; Buchanan, B.G., Shortliffe, E.H., Eds.; Addison-Wesley Publishing Company: Boston, MA, USA, 1984; pp. 832–838. [Google Scholar]
- Högger, A. Dempster Shafer Sensor Fusion for Autonomously Driving Vehicles: Association Free Tracking of Dynamic Objects; KTH Royal Institut of Technology School of Electrical Engineering: Stockholm, Sweden, 2016. [Google Scholar]
- Feng, R.; Zhang, G.; Cheng, B. An on-board system for detecting driver drowsiness based on multi-sensor data fusion using Dempster-Shafer theory. In Proceedings of the 2009 International Conference on Networking, Sensing and Control, Okayama, Japan, 26–29 March 2009; pp. 897–902. [Google Scholar]
- Jugade, S.C.; Victorino, A.C. Grid based Estimation of Decision Uncertainty of Autonomous Driving Systems using Belief Function theory. IFAC-PapersOnLine 2018, 51, 261–266. [Google Scholar] [CrossRef]
- Lu, C.; Wang, S.; Wang, X. A multi-source information fusion fault diagnosis for aviation hydraulic pump based on the new evidence similarity distance. Aerosp. Sci. Technol. 2017, 71, 392–401. [Google Scholar] [CrossRef]
- Yang, J.; Huang, H.-Z.; He, L.-P.; Zhu, S.-P.; Wen, D. Risk evaluation in failure mode and effects analysis of aircraft turbine rotor blades using Dempster–Shafer evidence theory under uncertainty. Eng. Fail. Anal. 2011, 18, 2084–2092. [Google Scholar] [CrossRef]
- Fontani, M.; Bianchi, T.; De Rosa, A.; Piva, A.; Barni, M. A Framework for Decision Fusion in Image Forensics Based on Dempster–Shafer Theory of Evidence. IEEE Trans. Inf. Forensics Secur. 2013, 8, 593–607. [Google Scholar] [CrossRef] [Green Version]
- Chandana, S.; Leung, H.; Trpkov, K. Staging of prostate cancer using automatic feature selection, sampling and Dempster-Shafer fusion. Cancer Inform. 2009, 7, 57–73. [Google Scholar] [CrossRef] [Green Version]
- Raza, M.; Gondal, I.; Green, D.; Coppel, R.L. Fusion of FNA-cytology and gene-expression data using Dempster-Shafer Theory of evidence to predict breast cancer tumors. Bioinformation 2006, 1, 170–175. [Google Scholar] [CrossRef] [Green Version]
- Denœux, T. 40 years of Dempster–Shafer theory. Int. J. Approx. Reason. 2016, 79, 1–6. [Google Scholar] [CrossRef]
- Denœux, T.; Smets, P. Classification using belief functions: Relationship between case-based and model-based approaches. IEEE Trans. Syst. Man. Cybern. B 2006, 36, 1395–1406. [Google Scholar] [CrossRef]
- Parzen, E. On Estimation of a Probability Density Function and Mode. Ann. Math. Stat. 1962, 33, 1065–1076. [Google Scholar] [CrossRef]
- Silverman, B.W. Using Kernel Density Estimates to Investigate Multimodality. J. R. Stat. Soc. Ser. B 1981, 43, 97–99. [Google Scholar] [CrossRef]
- Rosenblatt, M. Remarks on Some Nonparametric Estimates of a Density Function. Ann. Math. Stat. 1956, 27, 832–837. [Google Scholar] [CrossRef]
- Denœux, T. Decision-making with belief functions: A review. Int. J. Approx. Reason. 2019, 109, 87–110. [Google Scholar] [CrossRef] [Green Version]
- Denœux, T. Conjunctive and disjunctive combination of belief functions induced by nondistinct bodies of evidence. Artif. Intell. 2008, 172, 234–264. [Google Scholar] [CrossRef] [Green Version]
- Shafer, G. A Mathematical Theory of Evidence; Princeton University Press: Princeton, NJ, USA, 1976. [Google Scholar]
- Yang, J.B.; Xu, D.L. Evidential reasoning rule for evidence combination. Artif. Intell. 2013, 205, 1–29. [Google Scholar] [CrossRef]
- Yager, R.R. On the dempster-shafer framework and new combination rules. Inf. Sci. 1987, 41, 93–137. [Google Scholar] [CrossRef]
- Strang, G. Introduction to Linear Algebra; Wellesley-Cambridge Press: Wellesley, MA, USA, 2016. [Google Scholar]
- Tapia, J.F.D.; Tan, R.R. Ternary Diagram for Visualizing Epidemic Progression. Process Integr. Optim. Sustain. 2021, 5, 687–691. [Google Scholar] [CrossRef]
- Fleiss, J.L.; Levin, B.; Paik, M.C. Statistical Methods for Rates and Proportions, 3rd ed.; Wiley-Interscience: Hoboken, NI, USA, 2003; pp. 1–800. [Google Scholar]
- Smets, P. The Combination of Evidence in the Transferable Belief Model. IEEE Trans. Pattern Anal. Mach. Intell. 1990, 12, 447–458. [Google Scholar] [CrossRef]
- Smets, P.; Kennes, R. The transferable belief model. Artif. Intell. 1994, 66, 191–234. [Google Scholar] [CrossRef]
- Dubois, D.; Prade, H. The logical view of conditioning and its application to possibility and evidence theories. Int. J. Approx. Reason. 1990, 4, 23–46. [Google Scholar] [CrossRef] [Green Version]
- Smarandache, F.; Dezert, J. Proportional Conflict Redistribution Rules for Information Fusion. Adv. Appl. DSmT Inf. Fusion 2006, 2, 3–68. [Google Scholar]
- Chen, L.; Diao, L.; Sang, J. Weighted Evidence Combination Rule Based on Evidence Distance and Uncertainty Measure: An Application in Fault Diagnosis. Math. Probl. Eng. 2018, 2018, 5858272. [Google Scholar] [CrossRef]
- Sentz, K.; Ferson, S. Combination of Evidence in Dempster-Shafer Theory. In Sandia Report; Sandia National Laboratories: Albuquerque, NM, USA, 2002; Volume Sand 2002-0835. [Google Scholar]
- Barrett, T.; Edgar, R. Mining microarray data at NCBI’s Gene Expression Omnibus (GEO). Methods Mol. Biol. 2006, 338, 175–190. [Google Scholar] [PubMed] [Green Version]
- Edgar, R.; Barrett, T. NCBI GEO standards and services for microarray data. Nat. Biotechnol. 2006, 24, 1471–1472. [Google Scholar] [CrossRef] [PubMed]
- Irizarry, R.A.; Bolstad, B.M.; Collin, F.; Cope, L.M.; Hobbs, B.; Speed, T.P. Summaries of Affymetrix GeneChip probe level data. Nucleic Acids Res. 2003, 31, e15. [Google Scholar] [CrossRef] [PubMed]
- Rung, J.; Brazma, A. Reuse of public genome-wide gene expression data. Nat. Rev. Genet. 2013, 14, 89–99. [Google Scholar] [CrossRef] [PubMed]
- Van Vliet, M.H.; Reyal, F.; Horlings, H.M.; van de Vijver, M.J.; Reinders, M.J.; Wessels, L.F. Pooling breast cancer datasets has a synergetic effect on classification performance and improves signature stability. BMC Genom. 2008, 9, 375. [Google Scholar] [CrossRef] [Green Version]
- Bolstad, B.M. RMAExpress Users Guide. Available online: https://rmaexpress.bmbolstad.com/RMAExpress_UsersGuide.pdf (accessed on 26 March 2022).
- McCall, M.N.; Bolstad, B.M.; Irizarry, R.A. Frozen robust multiarray analysis (fRMA). Biostatistics 2010, 11, 242–253. [Google Scholar] [CrossRef] [Green Version]
- Gautier, L.; Cope, L.; Bolstad, B.M.; Irizarry, R.A. Affy—analysis of Affymetrix GeneChip data at the probe level. Bioinformatics 2004, 20, 307–315. [Google Scholar] [CrossRef]
- Stafford, P. Methods in Microarray Normalization; CRC Press: Boca Raton, FL, USA, 2008. [Google Scholar]
- McCall, M.N.; Jaffee, H.A.; Irizarry, R.A. fRMA ST: Frozen robust multiarray analysis for Affymetrix Exon and Gene ST arrays. Bioinformatics 2012, 28, 3153–3154. [Google Scholar] [CrossRef]
- Bolstad, B. Background and Normalization: Investigating the Effects of Preprocessing on Gene Expression Estimates. Available online: http://bmbolstad.com/stuff/BAUGM.pdf (accessed on 17 September 2021).
- Kenn, M.; Cacsire Castillo-Tong, D.; Singer, C.F.; Cibena, M.; Kölbl, H.; Schreiner, W. Microarray Normalization Revisited for Reproducible Breast Cancer Biomarkers. Biomed. Res. Int. 2020, 2020, 1363827. [Google Scholar] [CrossRef]
- Luo, J.; Schumacher, M.; Scherer, A.; Sanoudou, D.; Megherbi, D.; Davison, T.; Shi, T.; Tong, W.; Shi, L.; Hong, H.; et al. A comparison of batch effect removal methods for enhancement of prediction performance using MAQC-II microarray gene expression data. Pharm. J. 2010, 10, 278–291. [Google Scholar] [CrossRef] [Green Version]
- Leek, J.T.; Johnson, W.E.; Parker, H.S.; Jaffe, A.E.; Storey, J.D. The sva package for removing batch effects and other unwanted variation in high-throughput experiments. Bioinformatics 2012, 28, 882–883. [Google Scholar] [CrossRef] [PubMed]
- Müller, C.; Schillert, A.; Röthemeier, C.; Tregouet, D.A.; Proust, C.; Binder, H.; Pfeiffer, N.; Beutel, M.; Lackner, K.J.; Schnabel, R.B.; et al. Removing Batch Effects from Longitudinal Gene Expression-Quantile Normalization Plus ComBat as Best Approach for Microarray Transcriptome Data. PLoS ONE 2016, 11, e0156594. [Google Scholar] [CrossRef] [PubMed]
- Johnson, W.E.; Li, C.; Rabinovic, A. Adjusting batch effects in microarray expression data using empirical Bayes methods. Biostatistics 2007, 8, 118–127. [Google Scholar] [CrossRef] [PubMed]
- Leek, J.T.; Storey, J.D. Capturing heterogeneity in gene expression studies by surrogate variable analysis. PLoS Genet. 2007, 3, 1724–1735. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Leek, J.T.; Johnson, W.E.; Parker, H.S.; Fertig, E.J.; Jaffe, A.E.; Storey, J.D.; Zhang, Y.; Torres, L.C. sva: Surrogate Variable Analysis. 2017. Available online: https://bioconductor.org/packages/release/bioc/manuals/sva/man/sva.pdf (accessed on 26 March 2022).
- Parker, H.S.; Corrada Bravo, H.; Leek, J.T. Removing batch effects for prediction problems with frozen surrogate variable analysis. PeerJ 2014, 2, e561. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ikeda, K.; Horie-Inoue, K.; Inoue, S. Identification of estrogen-responsive genes based on the DNA binding properties of estrogen receptors using high-throughput sequencing technology. Acta Pharmacol. Sin. 2015, 36, 24–31. [Google Scholar] [CrossRef] [Green Version]
- McCullagh, P.; Nelder, J.A. Generalized Linear Models. In Monographs on Statistics and Applied Probability, 2nd ed.; Chapman & Hall: London, UK; CRC: New York, NY, USA, 1989; Volume 37. [Google Scholar]









| Number of Samples | DST | ||||
|---|---|---|---|---|---|
| neg | inc | pos | sum | ||
| ODDS | neg | 999 | 45 | 0 | 1044 |
| inc | 0 | 59 | 10 | 69 | |
| pos | 0 | 40 | 1366 | 1406 | |
| sum | 999 | 144 | 1376 | 2519 | |
| percentage | DST | ||||
| neg | inc | pos | sum | ||
| ODDS | neg | 39.7% | 1.8% | 0.0% | 41.5% |
| inc | 0.0% | 2.3% | 0.4% | 2.7% | |
| pos | 0.0% | 1.6% | 54.2% | 55.8% | |
| sum | 39.7% | 5.7% | 54.6% | 100.0% | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kenn, M.; Karch, R.; Cacsire Castillo-Tong, D.; Singer, C.F.; Koelbl, H.; Schreiner, W. Decision Theory versus Conventional Statistics for Personalized Therapy of Breast Cancer. J. Pers. Med. 2022, 12, 570. https://doi.org/10.3390/jpm12040570
Kenn M, Karch R, Cacsire Castillo-Tong D, Singer CF, Koelbl H, Schreiner W. Decision Theory versus Conventional Statistics for Personalized Therapy of Breast Cancer. Journal of Personalized Medicine. 2022; 12(4):570. https://doi.org/10.3390/jpm12040570
Chicago/Turabian StyleKenn, Michael, Rudolf Karch, Dan Cacsire Castillo-Tong, Christian F. Singer, Heinz Koelbl, and Wolfgang Schreiner. 2022. "Decision Theory versus Conventional Statistics for Personalized Therapy of Breast Cancer" Journal of Personalized Medicine 12, no. 4: 570. https://doi.org/10.3390/jpm12040570
APA StyleKenn, M., Karch, R., Cacsire Castillo-Tong, D., Singer, C. F., Koelbl, H., & Schreiner, W. (2022). Decision Theory versus Conventional Statistics for Personalized Therapy of Breast Cancer. Journal of Personalized Medicine, 12(4), 570. https://doi.org/10.3390/jpm12040570