Edge Pressures Obtained Using FEM and Half-Space: A Study of Truncated Contact Ellipses

Abstract

In rolling or gear contacts, truncation of the contact ellipse can occur, for example, when an undercut extends into the contact area. For an elastic calculation approach, the edge constitutes a mathematical singularity, which is revealed by a theoretically infinitely high pressure peak. However, when elastic–plastic material behavior is taken into account, the pressure peak is limited by local hardening and yielding of the material, leading to plastic deformations. As a result, those calculations are rather challenging and the results partly unexpected due to the discontinuity contained in the geometry. Nevertheless, to the authors’ knowledge, hardly any published studies exist on elastic–plastic simulations of truncated contact ellipses. Therefore, a numerical study concerning the contact of a rigid ball with an elastic–plastic plane is presented. Due to an undercut in the plane, a quarter of the theoretical Hertzian contact ellipse is cut off. The aim of the study is to investigate the influence of the undercut angle on the pressure distribution and the elastic and plastic deformation at the edge. The use of FEM shows that the undercut angle has a significant effect on the characteristics of the contact. The results obtained using FEM are then used as a reference for comparison with a semi-analytical method (SAM). It is shown that the SAM, based on the half-space, provides comparable results only for very small undercut angles.

1. Introduction

When dimensioning machine elements, the occurrence of stresses due to contact pressures exceeding the yield point is usually avoided or defined specifically to a very small extent by appropriate design. Nevertheless, situations occur in operation where an edge may come into the area of contact unintentionally. An example of this is truncation in rolling bearings: The rolling elements reach the rim of the raceway—for example, due to excessive axial load, shaft misalignment, or large deformations. The elliptical contact between ball and raceway is cut off. For the elastic calculation, the edge constitutes a mathematical singularity, which is revealed by a theoretically infinitely high pressure peak [1]. In reality, the infinitely high pressure peaks do not occur because metals have elastic–plastic material behavior. The high pressure leads to correspondingly high stresses and to yielding, i.e., plastic strains are formed and the material work-hardens. The strains manifest themselves in the form of local plastic deformations in an area near the surface, which modify the contact geometry and lead to a slight redistribution of the load. The pressures are thus limited. To estimate a possible early failure of the bearing, the knowledge of the correlation of pressures and plastic deformations at the edge is crucial.

However, even the elastic–plastic contact calculation of basic contact situations is rather challenging as soon as a discontinuity in the geometry is involved. An example of this is the contact between a rigid ball and an elastic–plastic plane containing an undercut (compare Figure 1).

The elementary contact between ball and plane is well known and can be calculated for the elastic case according to the formulas of Hertz [1,2]. Whereas analytical solutions are limited to some particular contact problems, numerical methods such as the finite element method (FEM) or the semi-analytical method (SAM) allow the calculation of any more complex contact geometries and the consideration of elastic–plastic material behavior. In particular, the idealized contact between ball and plane has been studied for many decades [3]. Either the ball or the plane is considered rigid [4,5], or both contact bodies can deform elastically or plastically [6]. In contrast, the special case of a truncated contact ellipse resulting in edge-pressures is hardly investigated.

If contacts containing edges are calculated, very fine local discretization is needed due to the high slope of the stress concentration. Using FEM, very high element numbers in return require high computing power. For this reason, the semi-analytical method (SAM) is becoming increasingly beneficial for contact calculations, as it allows for much faster computation [7] for many use cases compared to FEM. The SAM dates back to work by Jacq et al. [7] and has been further developed by many scientists for various applications, e.g., overrolling simulations [8,9,10,11,12] or the simulation of wear and fretting [13,14]. The SAM is based on half-space assumptions. Thus, the dimensions of the bodies must be very large compared to the contact zone, and the stresses must not depend significantly on the geometry of the contact partners at a significant distance from the contact zone. The bodies are considered in approximation as semi-infinite bodies, limited in their extension only by a plane [1]. In order to calculate bodies of finite length in half-space, a correction method was proposed by Hétenyi [15] and further developed by various scientists [16,17,18,19]. This is referred to as the quarter-space method. Najjari [20] extended the method to the calculation of stresses below the surface. However, with respect to the present problem of a contact ellipse truncated by an undercut, these approaches are insufficient. In the existing work on the quarter-space, elastic material behavior was assumed and the stress singularity caused by edge loading was not accounted for. Moreover, by definition, the quarter-space represents an edge with an angle of ${90}^{\circ }$. The contact calculation considering undercuts—for example, an angle of ${15}^{\circ }$, i.e., between half-space ($0^{\circ }$) and quarter-space (${90}^{\circ }$)—is thus apparently only possible by means of FEM.

To the authors’ knowledge, the discussion of a truncated elliptical contact considering elastic–plastic material behavior has not been addressed in literature, neither by using SAM nor by using FEM. Therefore, a numerical study was performed to analyze how the edge-pressure and plastic deformation manifest for a truncated contact. A rigid ball was pressed vertically onto an elastic–plastic plane with undercut, cutting off a quarter of the theoretical Hertzian contact ellipse (see Figure 1). The angle of the undercut $\alpha$ was varied, as the authors expect $\alpha$ to have a strong influence on the characteristics of the contact.

The study was first carried out using FEM, as it is not limited by the prerequisites of the half-space and thus allows for arbitrary geometries. The results were then used as a reference for comparison with SAM. The aim was to clarify the extent to which the results of the FEM can be reproduced with the half-space model. The existing quarter-space methods were deliberately not used, whereby deviations are expected due to the violation of the boundary conditions of the half-space by the undercut geometry.

2. Methods

2.1. Finite Element Method

The calculation and modeling were performed using the commercial FEM software Abaqus 3DEXPERIENCE R2018x HotFix 3. The Abaqus/Standard solver was used in a static simulation. The results were evaluated along the centerline of the contact at the surface. All results were evaluated for the non-deformed geometry. The plastic deformation $u_{pl}$ was evaluated as the deformation after unloading the contact and the total deformation u in fully loaded state. Elastic deformation $u_{el}$ was then calculated as the difference of total deformation and plastic deformation. The pressure distribution was evaluated in the loaded state.

2.2. Semi-Analytical Method

As no commercial or freely available software was used for the SAM, the calculation schema, see Figure 2, and the basic principles are briefly summarized below. For a more detailed description, please refer to [7,8,11].

SAM is based on the half-space assumptions, using semi-infinite bodies. The computational domain $\Gamma$ on the surface of the half space is discretized into $k\times l$ equal rectangular elements by an equidistant grid. For each surface element, an averaged value is calculated for each of the quantities of the contact problem. In the contact solver, the conjugate gradient method (CGM) [21] is used to solve the following coupled equations to calculate the load balance, Equation (1); the surface separation, Equation (2); and the contact conditions, Equations (3) and (4), which determine the contact area.

$$F={\int }^{}p(k,l)d\Gamma$$

(1)

$$h(k,l)=h_0(k,l)+\delta +u(k,l)\ge 0$$

(2)

$$h(k,l)=0,p(k,l)\ge 0\mathrm{if}(k,l)\in {\Gamma }_c$$

(3)

$$h(k,l)>0,p(k,l)=0\mathrm{if}(k,l)\notin {\Gamma }_c$$

(4)

The total applied load F corresponds to the integral of the pressure p over the computational domain $\Gamma$. The surface separation h is composed of the initial gap $h_0$, the rigid body displacement $\delta$, and the total surface deformation u. In the contact zone ${\Gamma }_c$, the surface separation is zero. Outside the contact zone, the surface separation is positive and the pressure is zero. Traction forces and deformations parallel to the surface are not considered in this work.

In the plastic loop, the 2D surface grid of the contact solver is extended perpendicular to the surface into a 3D computational domain that is meshed into constant-sized cuboid elements. For the cuboid elements, an average value is calculated for each of the stress and strain quantities. The elastic stresses are calculated directly from the pressure distribution on the surface [22]. The residual stresses can be calculated from the plastic strains that may be present [23,24]. Assuming small deformations and strains, the elastic and residual stresses can be superimposed. From the total stress state, a return-mapping algorithm [25] is used to calculate the change in plastic strains. Because a change in the plastic strain state results in a change in the underlying residual stresses, an iterative calculation is performed, as indicated by the name plastic loop. The plastic deformation of the surface can then be calculated from the converged strain state [7]. For the fast calculation of convolution products in the determination of residual stresses and plastic deformations, the discrete-convolution fast Fourier transformation DC-FFT [26] is applied.

As the plastic deformations locally change the contact geometry, the overall problem is solved iteratively in an outer loop between contact solver and plastic solver with a convergence criterion for the plastic deformation.

As shown in Figure 3, the geometry of the undercut is considered in the initial gap $h_0$. Thus, according to Equation (5), the geometry of the undercut $f(k,l)$ is added to the initial gap $h_0^{\prime }$ without undercut. In the contact solver, the undercut is thus correctly captured.

$$h_0(k,l)=h_0^{\prime }(k,l)+f(k,l)$$

(5)

While in the contact solver, the undercut can be captured even if it may violate the assumptions of the half-space; this is not possible in the plastic solver. The calculation of the plastic solver is done for the half-space independent of the surface separation h. The larger the undercut angle, the more the model deviates from the assumptions of the half-space. This is manifested by stresses and strains, which are calculated near the surface in the region of the undercut where there is actually no material. The extreme case is the undercut of 90°—the calculation is performed in the half-space, although it is a quarter-space.

To obtain the presented results for SAM, the software Telos from Schaeffler Technologies AG & Co. KG (Herzogenaurach, Germany) was used. Although Telos is not publicly available, similar results can be obtained with other SAM-based tools.

As was done with the results obtained using FEM, the plastic and elastic deformation as well as the pressure distribution obtained using SAM were evaluated along the center plane, which are directly available as output in the calculation tool used. As no tangential deformation in x and y direction is considered in the SAM, the outputs are best comparable with the outputs of the FEM for the undeformed geometry.

3. Model

In the presented study, a ball was pressed vertically onto a plane with undercut (see Figure 1). The ball was assumed to be rigid. The plane was modeled as AISI 52100 bearing steel with elastic–plastic material behavior. Young’s modulus and Poisson’s ratio were $E=210\mathrm{GPa}$ and $\nu =0.3$, respectively. The yield surface was modeled by isotropic strain hardening using Swifts’s law [27] according to Equation (6) in conjunction with the von Mises criterion. The hardening parameters for AISI 52100 were $B=945$, $C=20$, and $n=0.121$, with ${ϵ}_{\mathit{eff}}^p$ corresponding to the effective plastic strain [8,11]. The hardening curve is depicted in Figure 4.

$${\sigma }_y=B{(C+{10}^6\times {ϵ}_{\mathit{eff}}^p)}^n$$

(6)

The radius of the ball was $R=10$ mm. The load $F=90$ N was constant. For the classical elastic Hertzian point contact—i.e., without undercut—a maximum pressure of $p_H=2.1$ GPa and a half contact width of $a=0.143$ mm results. Those values are used to normalize all lengths and all stress values within this study. According to Hertz, in the elastic case, the selected load leads to a maximum von Mises equivalent stress of 96% of the yield point of the material. Thus, without truncation, yielding just does not occur. The choice of load seems reasonable, as plastic deformation for the complete contact ellipse is usually avoided by appropriate dimensioning.

Throughout this paper, the center of the coordinate system is fixed below the center of the ball on the surface of the undeformed plane. Whereas the x-axis and y-axis lie in the surface plane, the positive z-axis points perpendicular into the plane, as can be seen in Figure 1. The undercut had a sharp edge at $x=0.5a$. The angle of the undercut $\alpha$ was varied according to

Table 1. Values for the varied undercut angle $\alpha$.

↓  Half-Plane				←  Undercut Angle $\mathit{\alpha }$ in ${}^{\circ }$ →								Quarter-Space   ↓
0	0.5	1	1.5	2	3	5	10	20	30	40	50	60	70	80	90

in steps between $0^{\circ }$ and ${90}^{\circ }$. The two extreme values represent the half-space for $\alpha =0^{\circ }$ and the quarter-space for $\alpha ={90}^{\circ }$.

3.1. FEM Model

In Abaqus, the ball was defined as rigid. The contact was defined as node-to-surface and normal hard contact that was tangentially frictionless. As shown in Figure 5, the plane was divided into three increasingly finely meshed regions (I to III) connected by tie-constraints. The outer region (I) was modeled with a large size and a coarse meshing to meet the half-space characteristics in the FEM. The innermost region (III)—where contact occurs—was meshed with linear hexahedral elements of type C3D8S. Due to the expected stress concentration at the edge, a very fine discretization was chosen locally. Thus, an equidistant element length of $\Delta x=0.00156a$ in the x-direction, an equidistant element length of $\Delta y=0.05a$ in the y-direction, and an element length starting at $\Delta z_1=0.00187a$ with a bias towards $\Delta z_2=0.239a$ in the z-direction was defined. The selected mesh density was benchmarked for the purely elastic contact with the analytical Hertzian solution (see Figure 6a,b), and a mesh convergence study was performed. The result for an undercut angle $\alpha =3^{\circ }$ is shown in Figure 7. As shown schematically in Figure 5, the bottom surface of the outer region (I) was pinned, i.e., all translational degrees of freedom were disabled. To reduce the number of elements, the symmetry of the model to the xz-plane was utilised, i.e., only half the geometry was modelled and a corresponding symmetry boundary condition (fixed translation in y-direction and fixed rotation in x- and z-direction) was defined for all regions (I to III).

Figure 8a,b shows an enlarged section of the hexaeder-mesh at the edge. For an undercut angle of $\alpha =0^{\circ }$, i.e., without undercut (see Figure 8a), all hexaeder elements were undistorted cuboids. For higher undercut angles, the cuboid elements became visibly distorted in the undercut region $x>0.5a$ (see Figure 8b). To address this problem, a second meshing model was used for larger undercut angles (see Figure 9a,b). As can be seen in Figure 9a, the elements for meshing model 2 were undistorted cuboids for $\alpha ={90}^{\circ }$, whereas the distortion was stronger the smaller $\alpha$ was (see Figure 9b). To check the continuity of the two models, the meshing models overlapped for undercut angles $\alpha$ of ${40}^{\circ }$, ${50}^{\circ }$, and ${60}^{\circ }$.

3.2. SAM Model

Unlike in the FEM, in the SAM an equidistant discretization had to be applied for each of the three coordinate directions: $\Delta x=0.00156a$ in the x-direction, $\Delta y=0.05a$ in the y-direction, and $\Delta z=0.0156a$ in the z-direction. This potentially resulted in a very large element number. Whereas the two-dimensional elastic computational domain ${\Gamma }_{el}$ covered the entire contact region, the three-dimensional plastic computational domain ${\Gamma }_{pl}$ represented only a subset near the edge, as illustrated in Figure 10. This approach limited the element number in the computationally intensive plastic loop and thus made the computation time manageable. Due to the choice of load, significant plastic strains formed only in the region near the edge. The calculation of possibly existing small plastic strains and deformations in areas outside ${\Gamma }_{pl}$ were omitted in favor of the computation times. Analogous to the FEM model, the SAM model was benchmarked for the purely elastic contact with the analytical Hertzian solution (see Figure 6a,b), and a mesh convergence study was performed (see Figure 7).

4. Results and Discussion

In the following, the results obtained using FEM and SAM are presented and discussed. Special attention is paid to the characteristics of the pressure distribution p, the plastic deformations $u_{pl}$, elastic deformations $u_{el}$, and their dependence on the undercut angle $\alpha$.

4.1. FEM

Figure 11, Figure 12 and Figure 13 show the pressure distribution p, the profiles of plastic deformation $u_{pl}$, and elastic deformation $u_{el}$ at the surface in the x-z plane for undercut angles $\alpha$ from $0^{\circ }$ to ${30}^{\circ }$.

The undercut angle $\alpha =0^{\circ }$ represents the closed point contact between sphere and plane. According to Hertzian theory, the pressure p (Figure 11) as well as the normal elastic deformation $u_{z,el}$ (Figure 13a) showed a symmetric parabolic profile. The tangential elastic deformation profile $u_{x,el}$ (Figure 13b) was point symmetric with a change in sign near the contact center point, which indicates that the regions near the contact edge were elastically pulled towards the contact center. The plastic deformations $u_{pl,z}$ and $u_{pl,x}$ were zero, because the load was chosen in such a way that the material just did not yield in the absence of an edge.

As can be seen from the contact pressure distributions in Figure 11, for small undercut angles up to approximately $\alpha =5^{\circ }$, due to the elastic deformation, contact occurred in the region $x>0.5a$ despite the undercut geometry. The larger $\alpha$, the more the contact area was delimited. Additionally, a pressure peak, typical for truncated contacts, formed at the edge at $x=0.5a$. In a purely elastic calculation, this pressure would be theoretically infinite due to the mathematical singularity noted above. However, by considering elastic–plastic material behavior, the material starts to yield due to local high stresses. The material work-hardens according to the yield curve, and plastic strains build up. The plastic strains manifest in the form of permanent plastic deformations, which change the contact geometry and, together with the work-hardening of the material, limit the pressure peak. These plastic strains and deformations were present in a very small area near the surface at the edge where the very high stresses due to the pressure peak occurred. The illustration of the plastic deformations is therefore limited to the highly enlarged area around the edge in all figures throughout the paper. Following the theory, the larger plastic deformation $u_{pl}$ occurred, the larger the undercut angle $\alpha$ was chosen. The edge was thereby indented ($u_{pl,z}>0$), whereas in the undercut region a shoulder formed ($u_{pl,z}>0$) (see Figure 12a). The tangential plastic deformation $u_{pl,x}$ described a small displacement of the edge away from the contact center ($u_{pl,x}>0$) (see Figure 12b). Due to smaller contact areas for larger undercut angles $\alpha$, the elastic deformation $u_{el,z}$ increased in the contact area and decreased slightly in the non-contact area of the undercut (see Figure 13a). In the x-direction, the edge region was pulled towards the contact center to an increasing extent (see Figure 13b).

For undercut angles $\alpha$ from $5^{\circ }$ to approximately ${30}^{\circ }$, despite elastic deformations and local plastic deformations, the contact area no longer extended into the undercut region, i.e., $p=0$ for $x>0.5a$. The contact was sharply truncated. The magnitude of the pressure peak increased degressively, the larger the undercut angles $\alpha$ were chosen, to the maximum at $\alpha ={20}^{\circ }$ (see Figure 11). The rest of the pressure distribution hardly changed. Due to the higher pressure peaks and thus higher local stresses in the edge region, the plastic deformation $u_{pl}$ also increased, and the maxima of the plastic deformations $u_{pl,z}$ and $u_{pl,x}$ were reached for $\alpha ={30}^{\circ }$, as can be seen in Figure 12. The elastic deformations $u_{el,z}$ and $u_{el,x}$ followed this tendency (see Figure 13).

Figure 14, Figure 15 and Figure 16 show the pressure distribution p, the profiles of plastic deformation $u_{pl}$, and elastic deformation $u_{el}$ at the surface in the x-z plane for undercut angles $\alpha$ from ${30}^{\circ }$ to ${90}^{\circ }$.

Starting from $\alpha ={30}^{\circ }$ up to $\alpha ={70}^{\circ }$, the pressure distribution and the plastic deformation both showed an opposite behavior than before: The emerging pressure peak was smaller, the larger $\alpha$ was chosen (see Figure 14). In addition to that, the contact zone grew slightly on the side facing away from the edge. In accordance with the pressure, the plastic deformations $u_{pl}$ also built up to smaller magnitudes. Considering $u_{pl,z}$, for $\alpha ⩾{40}^{\circ }$, no shoulder, but only an indent at the edge was build up, and for $\alpha ={70}^{\circ }$, hardly any plastic deformation occurred (see Figure 15). Similarly, with a larger angle $\alpha$, a smaller tangential plastic deformation $u_{pl,x}$ occurred and was barely present at $\alpha ={70}^{\circ }$. As can be seen in Figure 16, the elastic deformation $u_{el}$ maintained its trend, with larger elastic deformations occurring for larger undercut angles $\alpha$. Particular attention should be paid to the elastic deformation $u_{el,x}$: as can be seen in Figure 16b, elastic deformations with negative magnitude were present up to $\alpha ={50}^{\circ }$ in the range of $x>0.5a$. For $\alpha ⩾{50}^{\circ }$, in contrast, larger elastic deformations occurred in the entire contact area, which also had a consistently positive magnitude for $x>0.5a$. Considering the coordinate system, this means that the entire contact area was pushed in the direction of the undercut.

For an undercut angle of $\alpha ={80}^{\circ }$, no pressure peak occurred at all. The magnitude of the pressure at the edge was smaller than its magnitude in the contact center. In the case of $\alpha ={90}^{\circ }$, the contact zone ended even before the edge (see Figure 14). Because there was no pressure peak with high local stresses, the yield point was not exceeded for these large undercut angles. Accordingly no plastic deformations $u_{pl,z}$ and $u_{pl,x}$ built up (see Figure 15). The contact stayed purely elastic. As can be seen in Figure 16, the elastic deformations $u_{el,z}$ and $u_{el,x}$, however, were maximum in comparison over all undercut angles $\alpha$.

The presented results obtained by using FEM show that the undercut angle has a significant influence on the characteristics of the contact for the considered model. This can be summarized and explained as follows: For very small angles $\alpha <5^{\circ }$, the undercut leads to a reduction of the contact area and for angles $\alpha ⩾5^{\circ }$ to a sharp truncation of the contact by the edge. As a result, the pressure distribution is delimited by a pressure peak at the edge at $x=0.5a$. Because the resulting locally occurring high stresses exceed the yield point, plastic strains and plastic deformations build up. These are characterized by an indentation of the edge and a small shoulder in the undercut region near the edge. The modification of the contact geometry and the hardening of the material limit the magnitude of the pressure peak. The normal elastic deformation in the contact increases slightly. In the tangential direction, there is only a very slight elastic deformation toward the contact center. For undercut angles $\alpha >{30}^{\circ }$, the larger $\alpha$, the lower the pressure peaks and the lower the plastic deformation. The elastic deformations, however, are even larger. The tangential elastic deformations $u_{el,x}$ illustrate that the whole edge is pushed away from the contact center—that is, the edge deflects elastically. This can be explained by the reduced structural stiffness of the undercut geometry for larger undercut angles. The observed enlargement of the contact area is consistent with those larger normal elastic deformations. For the considered model of this study, the elastic deflection effect reaches the point where for $\alpha ={90}^{\circ }$ the contact area does not even include the edge, so the pressure and the plastic deformations are zero at $x=0.5a$. The occurrence of this extreme case is of course dependent on the specific contact parameters, in particular the distance of the edge to the contact center.

The following generalized hypothesis can be derived: Very small and very large undercut angles can be considered rather uncritical. The large contact area for small angles and the deflection of the entire edge for large undercut angles prevent the occurrence of a significant pressure peak. No or very little plastification occurs at the edge. For the medium angle range, the contact area is limited by the undercut, but the structural stiffness of the edge geometry is too high to allow a relevant elastic deflection of the edge. Thus, the highest magnitude of the pressures peak and plastic deformations occur at medium undercut angles $\alpha$.

4.2. SAM

In the following, the results obtained by using SAM are presented. Again the pressure distribution p (see Figure 17), the normal plastic deformation $u_{pl,z}$ (see Figure 18), and the tangential elastic deformation $u_{el,z}$ (see Figure 19) were examined as in dependence of the undercut angle $\alpha$.

For an undercut angle of $\alpha =0^{\circ }$, i.e., the untruncated contact, the results were as expected: a symmetric parabolic pressure distribution p and elastic deformation $u_{el,z}$ as well as the absence of a plastic deformation $u_{pl,z}$.

For undercut angles up to ${20}^{\circ }$, the results obtained using SAM showed the same characteristic as the results obtained using FEM. The larger the angle $\alpha$, the smaller the contact area, until at $\alpha =5^{\circ }$ the contact was sharply delimited by the edge and the well-known pressure peak occurred (see Figure 17). In line with this, for larger undercut angles, the plastic deformation $u_{pl,z}$ formed an indentation at the edge and a small shoulder in the undercut area near the edge, as the yield point was exceeded locally (see Figure 18). The elastic deformation $u_{el,z}$ increased slightly in the contact area and decreased in the non-contact area of the undercut (see Figure 19).

For an undercut angle of ${20}^{\circ }$, the maximum values for the pressure and the plastic and elastic deformations occurred. The contact area remained almost constant. Remarkably, for $\alpha ⩾{20}^{\circ }$, both the pressure distribution and the profiles of the plastic and elastic deformation were constant regardless of the undercut angle. Thus, in Figure 17, Figure 18 and Figure 19, the curves for ${20}^{\circ }$ to ${90}^{\circ }$ are not shown separately.

The presented results obtained using SAM can be explained as follows: The SAM is based on the half-space. For the untruncated contact without undercut at $\alpha =0^{\circ }$, all relevant assumptions are fulfilled. The result is good, as expected. However, the larger the undercut angle $\alpha$, the more the assumptions of the half-space are violated. Nevertheless, by using the CGM in the contact-solver, the pressure distribution and the contact zone are well captured, as the undercut geometry is taken into account by the surface separation h (see Equations (2) and (5)). For an undercut angle $\alpha ⩾{20}^{\circ }$ the pressure distribution calculated in the contact-solver does not change, presumably because—despite a very fine discretization—no more differences are detected on the elastic grid even if the undercut angle is increased. The calculations of the plastic loop are only based on the pressure distribution. The undercut geometry itself and the reduced structural stiffness resulting from larger undercut angles are therefore not considered. This effect is further intensified because tangential deformations $u_{el,x}$—which represent the relevant elastic edge deflection as shown in the FEM—cannot be calculated. As the pressure distribution is constant for $\alpha ⩾{20}^{\circ }$, the model and thus the result no longer differ from the perspective of the plastic loop. The results of the SAM are therefore not plausible for larger undercut angles, as was to be expected.

4.3. Comparison of FEM and SAM

In the following, the results obtained using FEM and SAM, which were previously discussed separately, are compared. The results of the FEM seem plausible and are used as a reference for the evaluation of the SAM. With regard to the partially implausible results, it is to be answered to what extent the SAM is suitable for the calculation of truncated contacts. For this purpose, the pressure p, plastic deformation $u_{pl,z}$, and elastic deformation $u_{el,z}$ at the edge ($x=0.5a$) are plotted over the undercut angle $\alpha$ (see Figure 20, Figure 21 and Figure 22). Note the nonlinear ticks of the abscissa corresponding to Table 1.

As can be seen in Figure 20, the SAM and the FEM agreed well up to an angle of approximately $\alpha =3^{\circ }$. The pressure calculated by SAM for $\alpha =2^{\circ }$ was about $13\%$ and for $\alpha =3^{\circ }$ about $25\%$ higher than the value obtained using FEM. For larger angles, however, the results of the two methods diverged strongly qualitatively and quantitatively: In both models, the edge pressure increased up to the maximum for $\alpha ={20}^{\circ }$, but the obtained edge pressure using SAM reached an unrealistically high value of about $257\%$ of the value obtained using FEM and remained on this level as explained. In the FEM, however, the edge pressure dropped to zero at an angle of 90°.

The results of the two meshing models of the FEM showed the same results when overlapping: see Fem1 and Fem2 in Figure 20. This transition suggests that the simulation results were, as desired, independent of the different meshing.

In Figure 21, a comparable behavior can be seen analyzing the plastic deformation $u_{pl,z}$. In the range up to $\alpha =3^{\circ }$, there was good agreement between the SAM and the FEM. Whereas the maximum plastic deformation obtained using FEM was reached for $\alpha ={30}^{\circ }$ and then decreased again, the plastic deformation calculated by SAM showed a constant value for $\alpha ⩾{20}^{\circ }$. The maximum plastic deformation $u_{pl,z}$ built up using SAM was significantly lower than the maximum plastic deformation built up using FEM. The lower plastic deformation calculated in the SAM could be a contributory reason for the significantly higher edge pressure, as the contact geometry was not modified to the same extent as it was in the FEM.

As can be seen in Figure 22, the normal elastic deformation $u_{el,z}$ agreed well for FEM and SAM up to $\alpha ={40}^{\circ }$. Again, $u_{el,x}$ remained constant for the SAM, it increased strongly up to an undercut angle of $\alpha ={90}^{\circ }$ in the FEM, due to the decreasing structural stiffness that was only considered by the FEM.

The comparison of FEM and SAM reveals the strong deviation of the SAM from the FEM for larger undercut angles. For very small angles up to approximately $\alpha =3^{\circ }$, the boundary conditions of the half-space are satisfied quite well. The models agree well. The larger the undercut angle, the more noticeable the missing consideration of the tangential deformations in conjunction with the incapability to account for the reduction of the structural stiffness. In the plastic loop, inaccurate stresses and strains are calculated in the areas of the undercut, which result in inaccurate deformations at the surface, looping back to the pressure distribution. In conclusion, it must be stated that the SAM is unable to take into account the fact that high undercut angles tend to result in lower pressures and hardly any plastic deformation. However, this is crucial for the evaluation of truncated contacts.

The quarter-space method, which was not used here, is certainly an approach to improve the quality of results for very large undercut angles, because the quarter-space represents the contact geometry much better or meets it directly for $\alpha ={90}^{\circ }$. However, as can be concluded from the FEM results, it is the very small angles that are well captured by the half-space and the very large angles that are potentially well captured by the quarter-space that are not critical with respect to the edge pressure and plastic deformations. The relevant range of medium undercut angles, however, cannot be accessed so far by any of the methods based on the half-space.

5. Conclusions

This paper presents the results of a numerical study of the contact between rigid sphere and elastic–plastic plane, where due to an undercut, a quarter of the theoretical Hertzian contact ellipse is cut off. FEM calculation results reveal interesting characteristics of the truncated contact concerning pressure distribution and elastic and plastic deformation:

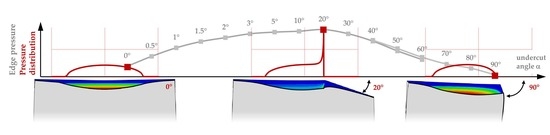
• Very small undercut angles can be considered uncritical. The contact area is slightly limited, but not yet completely delimited by the edge due to deformations. Only moderate pressure peaks and plastic deformations occur.
• For very large angles, the contact area is sharply limited by the edge. Due to the steep edge, however, the local structural stiffness of the plane is reduced to such an extent that the entire contact area can deform elastically to a relatively high extent. The edge deflects. Therefore, only minor or no pressure peaks and plastic deformations occur. The contact is significantly characterized by elastic deformation. Thus, also very large angles seem to be uncritical.
• Medium angle ranges result in the highest pressure peaks and plastic deformations, as the contact area is significantly limited by the edge, but the edge still has a high structural stiffness. Elastic deflection of the edge is only marginally possible.

The analysis of the results obtained using SAM and the comparison with the results obtained using FEM clearly revealed the weaknesses of the SAM with respect to the calculation of truncated contact ellipses. In particular, the plastic solver for calculating plastic strains and deformations cannot correctly represent the geometry of larger undercut angles by definition and thus leads to unrealistic results. The quarterspace method does not promise a better solution either, as the more critical medium angle range is located between the halfspace and quarterspace models. Thus, the application of the SAM to calculate truncated contacts seems to be unsuitable without more complex approaches or tricks, which still need to be developed.

The results presented and conclusions derived within this paper apply to the geometry considered in this study of a rigid ball on an elastic–plastic plane with undercut, that is, a truncated contact ellipse. Further studies should be conducted to determine whether these findings can also be applied to a truncated line contact, e.g., cylinder on plane with undercut.