CFD Modeling of the Effect of Different Surface Texturing Geometries on the Frictional Behavior

Abstract

In order to understand the effect of surface texturing parameters on the frictional behavior of textured surfaces and to correlate results of different lubrication regimes, Computational Fluid Dynamics (CFD) numerical analysis of the fluid flow was performed for four different textured surface geometries. The aim of the present research paper is to get theoretical background for the frictional behavior of textured surfaces under hydrodynamic lubrication. Since it is unrealistic to make a direct analysis of a real problem that can possess more than several thousand micro-dimples, the purpose is then to investigate the flow in single cells of periodical micro-dimple patterns and to extract useful conclusions for the lubrication’s framework. Among all geometries studied, optimum geometry shapes in terms of hydrodynamic performance were reported. It was found that the best hydrodynamic performance was achieved with the rectangular geometry (lowest shear force).

1. Introduction

1.1. Lubrication Theory

The purpose of lubrication is to generate a separating force between two closely spaced surfaces separated by a fluid in relative motion in order to reduce friction and wear. The separation and load-carrying capacity are achieved by generating a pressure in the fluid film between the surfaces [1]. For a good understanding of lubrication theory, three different regimes must be considered: boundary lubrication, mixed lubrication and hydrodynamic lubrication. If a full lubricating film is separating the surfaces and there are no asperities in contact, this regime is denoted as hydrodynamic or full-film. When hydrodynamic lubrication occurs, full film lubrication problems can be analyzed using the Reynolds equation to model the lubricant pressure and fluid flows, and the interaction between the lubricant and surfaces. However, due to an increasing availability of user-friendly, commercial CFD codes, there has been a growing application of the full Navier-Stokes equations to solve some lubrication problems [2].

If the amount of asperities in contact increases, the lubrication regime is denoted as mixed. In a mixed lubrication regime, modeling is more complicated since a full lubricating film does not exist and at the same time, only a part of the surface is in contact. Finally, when the load is carried by the asperities in contact, this is called a boundary lubrication regime. Thus, surface contact becomes the major part of the load-supporting mechanisms, and both plastic and elastic deformations occur. Some models on lubricant chemistry and contact mechanics do exist and can help to understand this lubrication regime. Therefore, contact under starved lubrication can be simulated using a Finite Element Model (FEM). The results obtained are valid for a “dry” sliding contact, but they may be extended to boundary-lubricated contacts with a small film thickness [3]. For large film thickness, FEM analysis is not valid since hydrodynamic effects would be dominant.

The three main lubrication regimes are illustrated schematically in Figure 1 in a typical Stribeck curve, that shows the evolution of the coefficient of friction “μ” with the non-dimensional parameter “H” that is defined as ηu/p, in which “η” is the lubricant dynamic viscosity, “u” is the velocity of the contacting surfaces and “p” is the mean contact pressure. H is strongly related to the film thickness.

As can be seen in Figure 1, at the right part of the Stribeck curve for high speeds, and/or lower loads, and/or consistent film viscosity conditions, the region could be associated with a hydrodynamic regime where friction increases almost linearly with H. It is thus realistic to assume that lubricant film is thick enough to fully support normal pressure during sliding. With diminishing H, friction coefficient reaches a minimum. The lubricant film thickness is reduced, revealing the limit of the hydrodynamic lubrication regime, and thus the beginning of the mixed lubrication regime. Consequently, for lower H, the surfaces in contact are supported on a combination of asperities and/or fluid. The left-hand section of the Stribeck curve is associated with the boundary lubrication regime where friction coefficient rises up to the quasi-static values in correspondence of critical pressure and/or vanishing sliding speed.

1.2. Modelling Textured Surfaces

Recent publications [1,4,5,6,7,8,9,10,11,12,13] have shown that the pressure-generating effect of textured surfaces that operate in full film lubrication conditions may be the result of three different mechanisms: micro-cavitation [5,6,7,8,12,13] that happens when the pressure in a fluid suddenly drops due to an enlargement of the flow section, convective inertia [1,9] that consists of the inertial force due to the convective acceleration in a flow, and piezo viscosity [10,11], a pressure dependence of viscosity. However, from all these mechanisms that happen in textured surfaces, it seems that micro-cavitation can make a decisive contribution in order to understand the load-carrying capacity effect.

Micro-cavitation can occur when the amplitude of the pressure variation, induced by the textured surface, is larger than the nominal pressure level at the particular location. Numerical simulations can account for micro-cavitation phenomena and thus help elucidate this issue. By using the Reynolds equation for an incompressible flow, the pressure variation in the surrounding area of the dimple should result in antisymmetry about a point located in a mid-plane (x = 0 and y = 0), since the pressure first decreases due to the channel height enlargement then increases under the influence of the diminishing transversal flow section at the right corner, as demonstrated by Sahlin et al. [1] where they showed a comparison between Navier-Stokes and Stokes solutions for the pressure distribution on the upper smooth wall for a cylindrical geometry. The usual practice is then to consider that the incompressible fluid will cavitate and pressures lower than the cavitation threshold are discarded in the calculation of the load-carrying capacity. One thus obtains a nonsymmetrical pressure distribution that leads to a lift effect that is exemplified in Figure 2. A second model proposed by Elrod and Adams [8] has as main advantage that it enforces mass conservation, which is not satisfied in the Reynolds model. However the Reynolds base method should be sufficient to illustrate the problem. In order to include inertia effects, the full Navier-Stokes equations have to be used instead of the Reynolds equations since the Reynolds equation does not incorporate convective inertia forces.

1.3. Simplifications to the Reynolds Equation

The Reynolds equation is a differential equation governing pressure distribution in a thin fluid film. This equation is frequently used in fluid film lubrication and in three dimensions can be written in the form [15]:

$$\frac{\partial }{\partial x}\left(\frac{h^3}{\eta }\frac{\partial p}{\partial x}\right)+\frac{\partial }{\partial y}\left(\frac{h^3}{\eta }\frac{\partial p}{\partial y}\right)=6\left(U\frac{\partial h}{\partial x}+V\frac{\partial h}{\partial y}\right)+12\left(w_h-w_0\right)$$

(1)

The terms on the left-hand side of the Reynolds equation represent the flow due to pressure gradients where ∂p/∂x and ∂p/∂y are the pressure gradients acting respectively along the “x” axis and along the “y” axis. The right-hand side shows the shear induced flow by the (top) surface sliding with velocity components U and V in the “x” and “y” directions, respectively. The second term on the right-hand side shows the flows induced by normal (squeeze) motions of the bounding surface where “w₀” is the velocity at which the bottom of the column moves up and “w_h” is the velocity at which the top of the column moves up. The film thickness is represented by “h” and “η” is the lubricant viscosity.

Some simplifications to the Reynolds equation are required before it can be used in practical engineering applications [15].

Unidirectional Velocity Approximation (It is always possible to choose axes in such a way that one of the velocities is equal to zero, i.e., V = 0) [15].

Assuming that V = 0, Equation (1) can be rewritten in a more simplified form:

$$\frac{\partial }{\partial x}\left(\frac{h^3}{\eta }\frac{\partial p}{\partial x}\right)+\frac{\partial }{\partial y}\left(\frac{h^3}{\eta }\frac{\partial p}{\partial y}\right)=6U\frac{\partial h}{\partial x}+12\left(w_h-w_0\right)$$

(2)

Steady Film Thickness Approximation (Movement of surfaces normal to the sliding velocity, known as a squeeze film effect, is not considered) [15].

It is always possible to assume that there is no vertical flow across the film, i.e., w_h − w₀ = 0. This assumption requires that the distance between the two surfaces remains constant during the operation. Assuming, however, that there is no vertical flow and w_h − w₀ = 0, Equation (2) can be written in the form:

$$\frac{\partial }{\partial x}\left(\frac{h^3}{\eta }\frac{\partial p}{\partial x}\right)+\frac{\partial }{\partial y}\left(\frac{h^3}{\eta }\frac{\partial p}{\partial y}\right)=6U\frac{\partial h}{\partial x}$$

(3)

Isoviscous approximation (This approach is known in the literature as the “isoviscous” model where the thermal effects in hydrodynamic films are neglected. However lubricant viscosity varies with thermal effects in hydrodynamic films and must be considered in a more elaborate and accurate analysis) [15].

For many engineering applications it is assumed that the lubricant viscosity is constant over the film, i.e., η = constant. Assuming that η = constant Equation (3) can further be simplified [15]:

$$\frac{\partial }{\partial x}\left(h^3\frac{\partial p}{\partial x}\right)+\frac{\partial }{\partial y}\left(h^3\frac{\partial p}{\partial y}\right)=6U\eta \frac{\partial h}{\partial x}$$

(4)

where the terms on the left-hand side of the Reynolds equation represent the flow due to pressure gradients and the right-hand side shows the shear induced flow by the (top) surface sliding with velocity U.

Or in dimensionless coordinates:

$$\frac{\partial }{\partial \overline{x}}\left({\overline{h}}^3\frac{\partial \overline{p}}{\partial \overline{x}}\right)+\frac{\partial }{\partial \overline{y}}\left({\overline{h}}^3\frac{\partial \overline{p}}{\partial \overline{y}}\right)=\frac{\partial \overline{h}}{\partial \overline{x}}$$

(5)

This is the most common form of the Reynolds equation used for solving engineering problems.

In the area outside the dimples the Laplace equation is applied:

$$\frac{{\partial }^2\overline{p}}{\partial {\overline{x}}^2}+\frac{{\partial }^2\overline{p}}{\partial {\overline{y}}^2}=0$$

(6)

The Laplace equation is also applied on the discontinuity nodes because the film thickness is considered to be equal with the film thickness of the nodes situated on nearby. The above equations are solved using the finite difference method.

1.4. Reynolds vs. Navier-Stokes Equation

One recurrently used approximation to the governing equations for fluid flow in tribology is the Reynolds equation, which is used in thin fluid films [16]. For a film thickness that is of the order or larger than the dimple depth (h_m/h_c ≥ 1), a large difference in pressure solution was found [4] between the Navier-Stokes and Reynolds equation. This is due to convective inertia. The magnitude of the pressure variation is relatively small and will not lead to micro-cavitation. For a film thickness that is small compared to the dimple depth (h_m/h_c < 1) the contribution of convective inertia becomes negligible. The amplitude of the pressure is large and micro-cavitation is almost certain to occur. In this last case the Reynolds equation can lead to a good approximation. However if the walls contain some geometrical perturbations, the inertial term can significantly influence the flow and the Reynolds approximations are not obvious as showed by Sahlin et al. [1].

1.5. Load-Carrying Capacity and Coefficient of Friction Equations

When the pressure distribution is integrated over the area of the cell surface the corresponding load-carrying capacity of the lubricating film can be calculated. Since including a cavitation model would increase the complexity and time consuming, a simple model (where pressures smaller than zero are forced to zero inside each iteration) was used. The real pressure occurring inside the contact is certainly higher than the pressure obtained without taking cavitation into account, but the difference is extremely small [3]. The mean pressure would be practically the same using the model with or without cavitation [3]. As a consequence the load-carrying capacity is calculated using only the positive values of the pressure:

$$\overline{F}={\displaystyle \underset{0}{\overset{L}{\int }}}{\displaystyle \underset{0}{\overset{L}{\int }}\overline{p}}\cdot d\overline{x}\cdot d\overline{y}$$

(7)

By definition the coefficient of friction is expressed as a ratio of the friction and normal forces acting on the surface:

$$\mu =\frac{F_f}{F}$$

(8)

where the friction force “F_f” generated due to the shearing of the lubricant is obtained by integrating the shear stress “τ” over the area of the cell surface.

$$F_f={\displaystyle \underset{0}{\overset{L}{\int }}}{\displaystyle \underset{0}{\overset{L}{\int }}\tau }\cdot dx\cdot dy$$

(9)

As was performed with load, coefficient of friction can also be expressed in a so-called normalized form. Therefore “μ” is defined entirely in terms of other non-dimensional parameters [17]:

$$\overline{\mu }=\frac{\overline{F_f}}{\overline{F}}=\mu \frac{L}{h_m}$$

(10)

The aim of the present research paper is to get theoretical background for the frictional behavior of textured surfaces under hydrodynamic lubrication.

2. Materials and Methods

2.1. Computational Fluid Dynamic (CFD) Analysis

Modeling using simplified the Reynolds equation showed that texturing provides pressure increase at the trailing edge of the dimples, which then creates lift force and consequently leads to reduced friction. However, in order to investigate in detail the effect of different texturing parameters and to get correlation with experimental results, computational fluid dynamic analysis (CFD) was carried out [18,19].

The present work was carried out by numerically integrating the full system of Navier-Stokes equations for a laminar, incompressible and isothermal flow in macro-roughness cells. Contact under full film lubrication was modeled through computational fluid dynamics (CFD) using FLUENT v6.3. Simulation of a fully wetted smooth plate sliding (u = 0.1 m/s) over a stationary groove separated by 5 μm of lubricating film was performed for 2D steady-state flow of viscous incompressible fluid (density 940 kg/m³, dynamic viscosity 1.06 kg/ms). In simulation, where periodicity in the direction of movement was taken into account (Figure 3 and Figure 4), a Semi-Implicit Method for Pressure-Linked Equations (SIMPLE) pressure velocity coupling was used. The SIMPLE algorithm, used to solve a steady-state problem iteratively, consists of the following steps [18,19]: (1) An approximation of the velocity field was obtained by solving the momentum equation and then the pressure gradient term was calculated using the pressure distribution from the previous iteration or an initial guess; (2) The pressure equation was formulated and solved in order to obtain the new pressure distribution; (3) Velocities were corrected and a new set of conservative fluxes was calculated. The convergence criteria was set to ε = 10⁻⁴.

The equations are steady and solved in the x- and y-direction only. The Navier-Stokes and the continuity equations can be written as follows:

In the x-direction,

$$\rho \left(u\frac{\partial u}{\partial x}+v\frac{\partial u}{\partial y}\right)=-\frac{\partial p}{\partial x}+\eta \left(\frac{{\partial }^{2}u}{\partial x^2}+\frac{{\partial }^{2}u}{\partial y^2}\right)$$

(11)

and in the y-direction,

$$\rho \left(u\frac{\partial v}{\partial x}+v\frac{\partial v}{\partial y}\right)=-\frac{\partial p}{\partial y}+\eta \left(\frac{{\partial }^{2}v}{\partial x^2}+\frac{{\partial }^{2}v}{\partial y^2}\right)$$

(12)

The continuity equation becomes:

$$\frac{\partial u}{\partial x}+\frac{\partial v}{\partial y}=0$$

(13)

where “u” and “v” are the components of the velocity vector, “x” and “y” are the coordinate directions, “p” is the pressure, “$\rho$“ the mass density, and “$\eta$“ the dynamic viscosity of the fluid.

2.2. Geometrical Model

Figure 3 represents the elementary textured cell considered in this study, and its geometrical parameters. In the case of cylindrical geometry the groove was described by a circular arc of defined depth and width, which are given in

Table 1. Individually varied parameters (with the standard fluid model indicated in “Bold”).

Varied Parameters	Geometry	Cavity Depth (μm)	Cavity Width (μm)	Spacing (μm)	Sliding Speed (m/s)
Study the influence of geometry	Cylindrical	22.8	128	500	0.1
	Rectangular	22.8	128	500	0.1
	Triangular	22.8	128	500	0.1
	Wedge	22.8	128	500	0.1
Study the influence of cavity depth	Cylindrical	8	128	500	0.1
	Cylindrical	16	128	500	0.1
Study the influence of cavity width	Cylindrical	22.8	40	500	0.1
	Cylindrical	22.8	80	500	0.1
Study the influence of spacing	Cylindrical	22.8	128	150	0.1
	Cylindrical	22.8	128	200	0.1
Study the influence of sliding speed	Cylindrical	22.8	128	500	0.01
	Cylindrical	22.8	128	500	0.05
	Cylindrical	22.8	128	500	0.2

. The length in the x-direction was defined by spacing (Table 1) and in y-direction set to 5 μm. The film thickness of the fluid field was set to 5 μm as predicted by Hamrock and Dowson equation [7] for given contact conditions.

In the present research work, four different textured geometries have been studied. The first geometry is the cylindrical geometry and can be seen in Figure 3. The other three geometries are: rectangular, triangular and wedge and are shown in

Table 2. Schematic representation of textured geometries.

Cylindrical
Rectangular
Triangular
Wedge

.

2.3. Varied Parameters

A standard fluid model (cylindrical geometry, depth = 22.8 μm, width = 128 μm, spacing = 500 μm and u = 0.1 m/s; light grey color in Table 1) was used as a reference and then certain parameters have been changed in a systematic order to investigate their effect on pressure distribution, velocity field and fluid flow. The influence of the cavity geometry (cylindrical, rectangular, triangular and wedge) in the flow characteristics was studied first, whereas the other reference conditions remain unchanged. A parametric study was performed by considering the cylindrical geometry and three different cavity depths, namely 8, 16, and 22.8 μm. The cavity width, spacing and sliding speed were kept constant within the reference conditions. The cavity width was also varied from 40 up to 128 μm and spacing from 150 up to 500 μm, whereas the other reference conditions remain unchanged. Finally, the effect of different sliding speeds (0.01, 0.05, 0.1 and 0.2 m/s) was also studied. The cylindrical geometry was used with cavity depth of 22.8 μm, cavity width of 128 μm and spacing 500 μm. A summary of the parameters that are being varied, entirely independently from one another, are listed in Table 1 and Table 2.

Although the form of the cavity can be described by a different number of parameters depending on whether it is rectangular, triangular, cylindrical, or wedge shaped, at least the peak to bottom distance (cavity depth) can be always defined and used for comparison of all shapes.

2.4. Boundary Conditions

In Figure 4, the boundary conditions for the fluid domain are presented. The fluid is experiencing no-slip conditions at the walls. The upper wall is moving with a velocity equal to u = 0.1 m/s while the lower wall is stationary (u = 0). Periodic boundary conditions are imposed on the left and on the right boundaries (edges at high and low x-coordinates) and a symmetry condition is applied in the z-plane. Periodic boundary conditions indicate that full periodicity in terms of field values and fluxes are ensured.

2.5. Computational Grid

Computational area was discretized with quadrilateral cells of a maximum length of 0.2 μm as shown in Figure 5. The discretization of 2nd order of pressure and 2nd order with upwinding of momentum as well as under-relaxation (pressure = 0.3, momentum = 0.7) were applied.

3. Results and Discussion

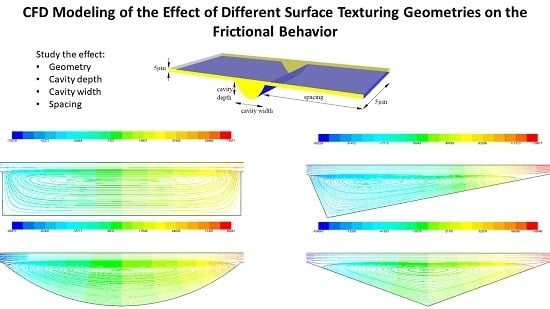
3.1. Influence of Cavity Geometry

Figure 6 shows streamlines and velocity vectors for the smooth surface. It can be seen that if the walls are parallel without a cavity, a simple Couette flow is to be found with an overall laminar flow of the viscous fluid in the space between the two parallel surfaces.

Streamlines for the four different groove geometries are shown in Figure 7a, Figure 8a and Figure 9a. It can be seen that the streamlines present the expected pattern with a recirculation zone located in the cavity. In the case of square-shaped cavity, the disturbance in streamlines is the most obvious and the largest followed by wedge shape, where asymmetry in streamlines can also be observed due to asymmetry in geometry. The smallest effect on fluid flow and the smallest vortex can be observed for triangular and semicircular type cavities. Figure 7b, Figure 8b and Figure 9b show the velocity field and illustrate how the vortex formation influences the inward fluid with a consequent development of a frontier layer next to the upper surface. This boundary layer does not expand to cover the dimples, so that a high-velocity gradient is maintained close to the moving surface even with deep dimples for the four different geometries. Figure 7c, Figure 8c and Figure 9c present the static pressure for the different geometries and show that pressure first diminishes at the left corner of the cavity and then increases when encountering the right corner. The pressure decrease and increase corresponds to an enlargement and to a diminishing transversal flow section. This is the well-known “ram effect” that occurs at rapidly converging constrictions. It can be seen that the static pressure is nearly symmetrical about a point located on the mid-section for the triangular, rectangular and cylindrical geometries. However for the wedge geometry the pressure rise is higher than the pressure drop as shown in Figure 10c.

Pressure variations on the upper wall are presented in Figure 11 for different geometries. The pressure first decreases due to the channel height enlargement at the left corner then increases when encountering the right corner due to the diminishing transversal flow section. The rectangular geometry produces lower amplitude of pressure distribution than the other three geometries. This was already seen in Figure 7c, Figure 8c and Figure 9c where the static pressure for the different geometries inside the cavity showed lower amplitude of values for the rectangular geometry (−75,079 to 74,971 Pa), followed by the cylindrical geometry (−89,271 to 89,261 Pa) and triangular geometry (−104,807 to 105,040 Pa). For the wedge geometry, due to asymmetry in geometry, the pressure rise was higher than the pressure drop (−85,229 to 139,817 Pa).

Following the pressure curves in Figure 11, the curves are entirely anti-symmetric about the point located at x = 0 and y = 0 for the rectangular, cylindrical and triangular geometry and the amplitude of the pressure distribution increases in the mentioned order with the curves being more sharp, whereas for the wedge geometry shows a net pressure rise in the domain. For the wedge geometry, the pressure distribution becomes asymmetric; namely, the pressure rise closer to the right corner being more important than the pressure drop.

In Figure 12 the shear force is plotted for the four different geometries (cylindrical, rectangular triangular and wedge). The rectangular geometry produces the lowest shear force between all the geometries investigated. This is in part explained by the fact that the rectangular groove inherits a greater area than the other three, using the same width and depth, which in turn gives rise to a lower friction force. Also, greater disturbances in fluid flow and greater vortex formation can be observed for rectangular geometry. As will be seen in next subsection (influence of cavity depth), the vorticity is clearly dependent on groove depth, increasing with its depth and giving rise to lower shear force.

3.2. Influence of Cavity Depth

Streamlines for different depths of semicircular cavity, shown in Figure 13, can give a qualitative idea about how the flow is organized and how it influences the hydrodynamic performance. In Figure 13a the streamlines are ordered and smooth, but as depth increases to a value of 16 and 22.8 μm, as can be seen in Figure 13b,c, a recirculation zone is developed in the cavity having closed contours. This shows that the vorticity/recirculation is clearly dependent on groove depth and increases with its depth.

The graphics, showing streamlines for the cylindrical geometry with cavity depths of 8 and 16 μm (Figure 13a,b, respectively), were already shown in a previous study [20] in order to illustrate the formation of the vortex inside the cavity, that are responsible for the shear force and global friction reduction. These were achieved by comparing fluid dynamic modeling with experimental tribological investigation showing friction results for different dimple depths.

Comparisons of pressure distribution for the cylindrical geometry are made in Figure 14, where the pressure is plotted as a function of the spatial dimension x for different values of cavity depth. The other parameters remain constant for all subfigures. Before arriving at the groove edge, located at x = −64 μm, pressure continues decreasing until it reaches the groove edge where the pressure curve suddenly changes to a pressure rise at a cavity depth of 8 μm. As already observed before, the total pressure rise is completely anti-symmetric to the total pressure drop, about a point located at y = 0 on the vertical midsection. As the depth of the cavity is increased it is clear that the pressure magnitude in the dimple region is decreased and change in pressure inside the cavity shifts away from linear to more exponential, as shown in Figure 14.

In Figure 15 the shear force in the lubrication film is plotted for three different cavity depths. As shown, the shear force decreases when the dimple depth increases from 8 to 22.8 μm. The result is lower friction and thus a reduced friction coefficient. Thus, a minimum value of F_x = 0.46 N is found for a cavity depth of 22.8 μm. However to obtain a true estimate of the performance benefit of the cavity, comparison should be made between a grooved surface and a smooth surface, under the same contact conditions. The shear force, for a smooth surface (cavity depth is set to zero), corresponds to a value of F_x = 0.55 N, with the result that the 22.8 μm deep cavity produces a considerable overall reduction of 16 % in shear force and gives rise to lower friction.

Hydrodynamic efficiency depends on load-carrying capacity (normal wall force) and shear force (tangential wall force), respectively, in the y- and x-direction. As seen in the previous section, the load-carrying capacity results from the integration of the pressure distribution over the area of the cell surface. If considered a simplified cavitation model where pressures smaller than zero are forced to zero it can be concluded that the highest load-carrying capacity is achieved by using dimple depth of 8 μm and is decreasing as dimple depth increases. At the same time, it is seen that the shear force is also monotonically decreased by increasing values of dimple depth, due to a local increase in film thickness. It can be seen that a recirculation zone occurs in the dimple when the depth increases from 8 to 16 μm. Increasing the depth of the dimples tends to generate a stretched recirculation zone. According to Shankar et al. [21] this backflow leads to a lower pressure gradient and lower pressure generation, which can explain the obtained results for pressure distribution. Since the main objective is to achieve as high a load-carrying capacity at as low a shear force as possible, the increase of dimple depth gives contradictory results for this range of dimple depth variation. However, the decrease in shear force with the increase in dimple depth from 8 to 22.8 μm is also in agreement with the experimental results published in previous papers from the same authors [22]. For higher sliding speeds, especially at 0.45 m/s where the contact is under full film lubrication, as the dimple depth increases friction gets reduced as shown in previous studies performed by Vilhena et al. [22], where they showed the variation of the coefficient of friction with the cavity depth.

3.3. Influence of Cavity Width

In Figure 16, streamlines are plotted for the cylindrical geometry with constant depths but different widths. At a sufficiently small value of width (see Figure 16a) no vortex and no back-flow exists in the groove anymore. As width increases to a value of 80 μm, see Figure 16b, a recirculation zone is developed in the cavity. It can be seen that the vortex decreases in size as the cavity width increases from 80 to 128 μm.

Comparisons of pressure distribution for the cylindrical geometry are made in Figure 17, where the pressure is plotted as a function of the spatial dimension x for different values of cavity width. The same observations hold for the pressure distribution presented in Figure 14. The distribution is anti-symmetrical about the x = 0 and y = 0 midsection. However, it is clear that the amplitude of the pressure variation in the dimple region and the maximum pressure at the dimple edge increases with increasing width.

Figure 18 shows how the shear force is affected by different values of cavity width for the cylindrical geometry. As the cavity width increases, the shear force, F_x decreases monotonically. When compared to un-textured or smooth surface, a drop in shear force for 40 μm wide grooves is only about 5%. However, as the width increases to 80 and 128 μm wider groves, reduction in shear force increases to 10 and 20%, respectively.

The best hydrodynamic performance is achieved for cavity width of 128 μm since the shear force decreases with increasing values of cavity width and the load-carrying capacity, which can be related to the amplitude of the pressure distribution on the flat moving wall, increases with cavity width as well.

3.4. Influence of Distance between Cavities (Spacing/Density)

In Figure 19, streamlines are plotted for the cylindrical geometry with constant depth and width but for different spacing. As the spacing increases vortex is shifted closer to the cavity surface. It can also be observed that as the distance goes from 150 to 250 μm and then to 500 μm, vortex changes its shape becoming more “flat” and narrow, with only a thinner section/layer affected by the vortex.

Pressure variations on the upper wall are presented in Figure 20 for different distances between cavities (spacing). As for all cases, the pressure first decreases due to the channel height enlargement then increases under to the influence of the diminishing transversal flow section at the right corner. However, it can be seen that the distance between cavities influences the amplitude of the pressure variation and the pressure curves are convexly shaped across the left half of the dimple and have concave shapes at the right half, with the curve for 250 μm spacing, showing extreme convexity and concavity and lower amplitude variation.

Since a reference pressure must be imposed in a point of the fluid field, and the resulting pressure field is computed with respect to this imposed value (zero in this case). By imposing different spacings, we are shifting the periodic boundary conditions and the reference pressure is considered at different locations. Consequently, a longer pressure cycle is obtained in case where spacing is 500 μm (blue line in Figure 20), while a shorter cycle is obtained in case where spacing is 250 or 150 μm (yellow line in Figure 20).

In Figure 21, the shear force is plotted as a function of distance between cavities (spacing). There exists an optimal value of spacing in terms of shear force that could fit in the range 150 < spacing < 500.

Making a comparison between Figure 19, Figure 20 and Figure 21 reveals the relationship between vortex formation, amplitude of the pressure distribution and shear force in terms of different values of spacing. This discussion shows that the minimum shear force and minimum amplitude of pressure distribution appears at a certain value of vorticity represented by more spaced streamlines, which means that lower velocity can be found.

This simulation is in agreement with the experimental results from previous studies performed by Podgornik et al. [20], where they showed the variation of the coefficient of friction with the cavity density. At higher sliding speeds, as the lubricant fluid film thickness increases and the contact enters the full fluid film lubrication regime, an optimal value of density in terms of coefficient of friction, that could fit in the range between 3.5 % (300 μm spacing) and 31.2 % (100 μm spacing), was observed. The minimum coefficient of friction was obtained for 7.8 % density (200 μm spacing).

3.5. Influence of Sliding Speed

Figure 22 shows the variation of shear force at different sliding speeds. It is shown that the shear force also monotonically increases by increasing the sliding speed, for a given thickness. For very small sliding speeds, when viscous effects are dominant the shear force is very small; with the augmentation of the sliding speed and the increased importance of inertia forces the shear force increases exponentially. However, in real contacts, lubrication film thickness is not constant and is a function of viscosity, sliding speed, and applied load. This, in turn, determines the lubrication regime. As sliding speed increases, the film thickness also increases and starts to move from “boundary” where the two surfaces mostly are in contact with each other and results in very high friction, to “mixed” where the two surfaces are partly separated, partly in contact and a sharp drop in coefficient of friction is observed, and, finally, to full film or hydrodynamic lubrication where the two surfaces are separated by a fluid film and the coefficient of friction reach its minimum. However in hydrodynamic lubrication the coefficient of friction slightly increases with sliding speed. This is due to the friction produced by the fluid. At higher sliding speeds, the fluid film becomes thicker. However, the fluid drag on the moving surfaces also increases, which can explain the results shown in Figure 22. Therefore, Reynolds and Computational Fluid Dynamics (CFD) analysis of fluid flow between parallel surfaces are only valid when contact is under full film lubrication.

Strong similarities between CFD analysis of textured surfaces presented in this study and results reported by Sahlin et al. [1] can be further underlined. Thus, Sahlin et al. [1] analyzed the influence of micro-patterned surfaces in hydrodynamic lubrication. Their calculations were made for two types of parameterized grooves with the same order of depth as the film thickness. They show that an introduction of a micro groove with a given geometry on one of the surfaces affects the fluid flow and pressure pattern and that the shear force decreases with increasing values of groove depth and width. It was also noticed that shear force increased with Re number. These results corroborate entirely our CFD simulation (see Figure 22). They also show that load-carrying capacity increases with groove width and a general optimum is achieved when dimensionless groove depth (d⁺) is in between 0.5< d⁺ <0.75. However, for dimensionless groove depth higher than 0.75 it was shown that an increase in groove depth leads to a decrease in load-carrying capacity. This agrees with our experiments since the magnitude of pressure distribution decreases with increasing dimple depth in the range of 8, 16 and 22.8 μm (dimensionless dimple depth of 1.6, 3.2 and 4.6 for a given film thickness of 5 μm). Based on our experiments and Sahlin et al. results [1], it can be concluded that if the depth is below some critical value, the increase of dimple depth increases the load-carrying capacity. If it is above, contributes to a reduction of the load-carrying capacity.

4. Conclusions

A limited number of analytical models to study surface texturing have been proposed [1,2,4,19,23], mostly considering hydrodynamic effects of micro-texturing, while the majority of studies have been experimental by trial and error approach [20,21,22,24,25,26]. For full film lubrication, another frequently used approximation to the governing equations for fluid flow is the Reynolds equation where the inertia term is neglected. The current work is based on the full system of Navier-Stokes equations and provides the following conclusions:

• For low Reynolds numbers, an analogous result can be obtained using the Reynolds and the Navier-Stokes equations since the pressure distribution is anti-symmetrical about the point located at the mid-plane of the cell, as shown during the present investigation. However, for large Reynolds numbers the pressure distribution becomes asymmetric, resulting in a positive net force, which requires the use of the Navier-Stokes equation.
• The CFD simulation performed in this research work discussed only the effect of the shear stress due to the presence of the micro-dimple. However, for the conditions simulated in this study (high viscosity fluid), the Reynolds number, Re << 1 shows that the convective inertia forces can be neglected. (The Reynolds number is defined as Re = ρuh/μ where ρ and μ are the density and dynamic viscosity of the fluid, h the film thickness and u is the velocity of the moving wall.) Although these results need further investigation, they clearly indicate that optimization of surface texturing for full-film lubrication can be done through CFD.
• An introduction of a micro-groove on one of the surfaces affects the flow and pressure distribution. For very small Reynolds numbers, when viscous effects are largely dominant and the approximation of the Stokes flow regime is acceptable, the pressure distribution is anti-symmetrical about the point located at x = 0 and y = 0. The shear force is also monotonically decreased by increasing values of cavity depth, due to a local increase in film thickness. The result is lower friction and thus a reduced friction coefficient. This agrees with our CFD simulation since the magnitude of pressure distribution decreases with increasing dimensionless dimple depth from 1.6 to 3.2 and 4.6.
• CFD simulation for different distances between cavities (densities) is also in agreement with the experimental results obtained under full-film lubrication in previous work [20]. They clearly showed that there exists an optimal value of spacing in terms of shear force. Furthermore, according to the CFD simulation the best hydrodynamic performance is expected with the rectangular geometry (lowest shear force).