Design Optimization of an Automotive Turbocharger Thrust Bearing Using a CFD-Based THD Computational Approach ^†

Abstract

In a quest to reduce fuel consumption and emissions of automotive combustion engines, friction losses from many different sources need to be minimized. For modern designs of turbochargers commonly used in the automotive industry, reduction of friction losses results in better efficiency and also contributes to a faster transient response. The thrust bearing is one of the main contributors to the mechanical losses of a turbocharger. Therefore, it is crucial to optimize the design of the thrust bearing so that it has minimum friction losses while keeping sufficient thrust carrying capacity. One of the main challenges of turbocharger thrust bearing design, is that rotation speed is not fixed: the turbocharger may have a rotation speed which varies between 0 to as much as 250 kRPM. Moreover, the thrust bearing generates considerable heat, which changes the temperature of the oil film and its surroundings. In the present work, the design of the thrust bearing of an automotive turbocharger has been optimized. A CFD-based Thermohydrodynamic (THD) computational approach has been developed, taking into consideration heat dissipation, conjugate heat transfer throughout the bearing domain including the surrounding parts, as well as shear thinning and cavitation in the lubricant domain. An optimizer has been coupled to the CFD solver, with the aim of identifying bearing designs with reduced friction losses. Two bearing concepts have been evaluated: a taper-land design—which is a commonly applied thrust bearing concept—as well as a pocket bearing design. The resulting optimum pocket designs exhibit improved performance, in comparison to the optimum taper-land design. The present results indicate that (a) the pocket design concept can substantially contribute to further reducing the friction losses of a turbocharger, and (b) optimal design parameters of pocket bearings depend on the specific application (size, operating conditions), therefore detailed calculations should be performed to verify optimum performance.

1. Introduction

Turbochargers have enabled combustion engines to become smaller and more efficient while remaining equally powerful. The amount of turbocharged gasoline passenger vehicles has grown considerably the past decades. Moreover, almost all diesel engines for passenger vehicles are nowadays equipped with turbochargers [1]. A turbocharger is basically a rotor that features a turbine on one side and a compressor on the other side (Figure 1). The turbine scavenges energy from the exhaust gas flow and delivers it to the compressor, which compresses ambient air and feeds it to the engine. As the density of the air is increased by compression, more air can be admitted at each combustion stroke and hence more power can be made [2].

Turbochargers operate at high rotational speeds, with maxima typically well over 200 kRPM. To support the rotor at these rotation speeds, either ball bearings or fluid film bearings are used. Although fluid film bearings have, in general, higher friction losses than ball bearings, their low-cost price (when produced in large volumes) and their lower sensitivity for out of balance induced vibrations and consequent whining noise render them the bearing type of choice for the vast majority of passenger vehicle turbochargers [2,3,4]. The fluid film bearing system of a turbocharger commonly consists of semi- or full floating ring bearings for radial support as well as a tapered-land thrust bearing for support in axial direction [5].

The thrust bearing carries the following two thrust loads [2]:

• the static pressures acting on the compressor wheel and the turbine wheel.
• the change of momentum of the air flowing from axial direction to radial direction in the compressor and vice versa for the turbine.

Depending on the operating condition of the turbocharger, the static thrust load is either directed towards the turbine or towards the compressor. Therefore, the thrust bearing is two-sided: it contains a taper-land profile at both sides of the bearing. Furthermore, as the exhaust gas flow of a combustion engine is mostly a pulsating flow, consequently the thrust load has a relatively high dynamic component [6].

Minimization of friction losses is generally pursued to increase turbocharger efficiency and to decrease transient response times. Particularly at low engine speeds, turbocharger friction losses play a significant role [7], contributing to the well-known turbo lag [8]. Depending on the operating conditions and the design of the bearing system, the thrust bearing may be responsible for roughly half of the total friction losses of the bearing system [7,9]. Therefore, the friction losses of turbocharger thrust bearings have already been studied extensively [7,8,9,10,11,12,13,14].

One of the ways to reduce the friction losses in a turbocharger thrust bearing is by application of surface texture features. Recent research has been carried out to investigate the effect of periodic irregularities of various shapes (rectangular, trapezoidal, cylindrical or spherical), imprinted on part of the stator of fixed inclination thrust bearings on bearing performance. The reported numerical [15,16,17,18,19,20,21,22] and experimental studies [23,24,25], demonstrated potential for improving bearing performance. As current technology has enabled the accurate manufacturing of such micro-scale patterns, contemporary research on the performance of textured bearings is growing more intense, with the optimization of texture geometry and placement being attempted by several researchers [5,6,7,8]. Apart from research aiming at identifying the potential of surface texturing to fixed pad thrust bearings, relevant studies on pivoted-pad thrust bearings have also been reported [26,27,28,29,30], showcasing substantial performance improvements in terms of increased load carrying capacity and reduced power losses.

Detailed modeling is required for accurate representation and study of thrust bearings. In general, the use of the Reynolds equation gives satisfactory results for problems of hydrodynamic lubrication of interacting surfaces with simple geometry and low values of rotation speed. However, for more complex geometries (such as textured geometries) and high values of rotational speed, additional phenomena need to be taken into consideration. The applicability of the Reynolds equation for textured, infinite-width sliders has been investigated in [31], where it was shown that its validity cannot be decided by the Reynolds number alone, as the geometric parameters of surface texturing (in particular the texture length-to-depth ratio) may have an equally important influence. Generally, the use of Navier-Stokes equation solvers has lately become increasingly popular for accurate flow analysis of fluid bearings. In particular, detailed CFD numerical analyses can be advantageous since (a) they provide increased calculation accuracy in cases with relatively high values of Reynolds number, especially for highly loaded thrust bearings and high values of rotational speed, (b) heat dissipation in the lubricant domain and heat transfer through the bearing and rotor solid can be efficiently simulated, and (c) flow phenomena in the bearing groove region can be accurately calculated by simulating the mixing of hot oil at the pad outlet with cold oil fed to the groove region (i.e., by detailed simulation of the hot-oil-carry-over phenomenon) [32]. Further, lubricant behaviour at extreme conditions, in particular dependence of oil viscosity on temperature and pressure [33], cavitation [34,35,36] and shear thinning can be simulated in detail, adding to the complexity of the built models and to the required computational time. In the literature, several optimization techniques have been suggested for refining bearing design, either in terms of macroscopic geometric design parameters, [37,38,39], or by introducing artificial surface texturing [21,22].

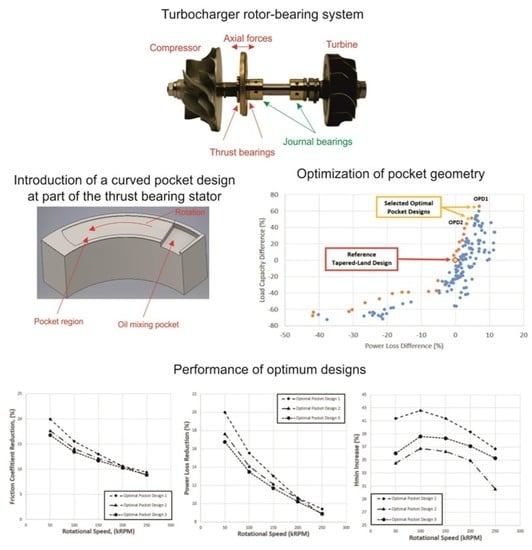
In the present work, a design optimization study of two different configurations of automotive turbocharger thrust bearings is performed. In particular, the two different configurations studied are a conventional taper-land bearing and a curved pocket bearing design. For both bearing configurations, a parametric CFD-based THD model is generated, capable of accounting for heat dissipation, conjugate heat transfer throughout the bearing domain including the surrounding parts, as well as shear thinning and cavitation in the lubricant domain. A design optimization problem is stated, seeking sets of design (geometric) variables that optimize the frictional behaviour of the bearing. Finally, the optimization results are evaluated for determination of bearing designs that exhibit low friction losses, while maintaining reliable operational characteristics.

2. Problem Setup

In the present work, a thermohydrodynamic (THD) approach is utilized for the study of a low-load, high-speed turbocharger thrust bearing. The present approach is based on CFD instead of the conventional Reynolds equation. Turbocharger thrust bearings are characterized by high values of rotational speed and oil temperature. Therefore, fluid inertia may play a role [8], which is conveniently included by utilising the Navier-Stokes equations. In the present study two different thrust bearing designs are analysed, in particular (a) a tapered-land thrust bearing and (b) a pocket thrust bearing. For the optimization process, reference bearing designs have been selected based on parametric analyses utilising the Reynolds equation. Further, parametric CFD-based THD models have been generated, and optimization simulations have been carried out utilizing an in-house optimizer based on genetic algorithms.

2.1. Bearing Geometries

The thrust bearing configurations investigated in the present study consists of four sector pads. The bearings main geometric parameters are given in

Table 1. Thrust bearing geometry parameters.

Geometric Parameter	Inner Diameter	Outer Diameter	Pad Area	Pad Thickness	Rotor Thickness
Value	7.5 mm	10.5 mm	9.79 mm2	2.73 mm	2 mm

. Regarding the tapered-land bearing geometry, a wedge-shaped geometry of the lubricating film is generated between the tapered part of the pad and the rotor, which leads to pressure buildup. The remaining part of the bearing is parallel to the rotor surface. Circumferentially, at the outer part of the pad, a lip is present in order to reduce side leakage and pressure drop at the high-pressure region of the bearing (Figure 2). The shape and dimensions of the tapered-land bearing was such that an automatic mesh procedure was not feasible. It is noted that an automated meshing procedure is essential for performing unattended design optimization. To overcome this issue, an equivalent slider geometry has been generated, with main dimensions identical to those of a single bearing pad (Figure 3). In order to better approach the physics of the bearing geometry, the velocity of the fluid in the fluid-rotor interface has been set as proportional to the radial coordinate, to accommodate the velocity variation that is observed in the thrust bearing geometry. However, the total area of the generated slider cannot be equal to that of the reference bearing, thus, differences in performance are expected. To this end, for performance comparisons, a reference slider bearing has been assumed; all optimal tapered-land designs are presented in comparison to the reference slider design.

The curved pocket bearing geometry (Figure 4) corresponds to a simple plain parallel bearing geometry, featuring a pocket geometry with circular circumferential edges, a straight radial aft edge and a circular radial fore edge. The curved pocket bearing features an oil inlet groove in the inner surface of the bearing in order to be able to have a large inflow of fresh low temperature oil, and avoid cavitating conditions at the oil inlet region due to starvation.

2.2. Numerical Model

The conservation equations, solved with the CFD code ANSYS CFX for steady, incompressible flow, with zero gravitational and external body forces, are:

Mass conservation equation:

∇⋅V = 0

(1)

Momentum equations:

ρ(V⋅∇)V = −∇p + ∇⋅(μ·∇V)

(2)

Energy equation, fluid domain:

ρc_pf V⋅∇Τ = ∇⋅(λ_f·∇Τ) − τ:∇V

(3)

Energy equation, solid domains:

∇⋅(λ_s·∇Τ) = 0

(4)

where, V is the fluid velocity vector (m/s), p is the fluid pressure (Pa), T is the fluid/solid temperature (K), τ is the viscous stress tensor (Pa), ρ is the oil density (kg/m³), μ is the oil dynamic viscosity (kg/(m·s)), c_pf is the oil specific heat capacity (J/(kg·K)), λ_f is the oil thermal conductivity (W/(m·K)), and λ_s corresponds to the thermal conductivity of the pad and the rotor (W/(m·K)).

In the present work, the utilized values of thermophysical properties for the lubricant are given in

Table 2. Lubricating oil parameters.

Oil Parameters
Symbol	Value	Units	Comments
ρ	855	Kg·m3	Oil density
c	2.1	kJ/(kg·K)	Heat capacity
k	0.145	W/(m·K)	Thermal conductivity
A	0.44	mPa·s	Temperature coefficient.
B	633	°C	Temperature coefficient
C	88.6	°C	Temperature coefficient
rl	0.5	-	Shear rate coefficient
m	0.8	-	Shear rate coefficient
K	7.2 × 10−7	s	Shear rate coefficient

. In particular, a 5W30 lubricant is assumed, characterized by a density value of 855 kg/m³, whereas the rheological properties of the lubricant are described using the Vogel equation for the dependence of viscosity on temperature T and the Cross equation to describe the shear-rate influence on viscosity, according to the following relation [10]:

$$\mu (T,\dot{\gamma })=A{\mathrm{e}}^{B/(T+C)}(r_1+(1-r_1)/(1+(K\dot{\gamma }{)}^m))$$

(5)

where $\dot{\gamma }$ is the strain rate of the lubricant, c the specific heat capacity and k the thermal conductivity. Parameters A, B, C, r, m and K characterizing the rheological behaviour of the present lubricant are also given in Table 2 [10]. The thermophysical properties of the solid components of the bearing (rotor/stator) are presented in

Table 3. Thermophysical properties of the pad and rotor materials.

Property	Pad Material	Collar Material
Specific Heat Capacity	434 (J·kg−1·K−1)	434 (J·kg−1·K−1)
Thermal Conductivity	122 (W·m−1·K−1)	50 (W·m−1·K−1)
Molar Mass	61 (kg·kmol−1)	55 (kg·kmol−1)
Density	8470 (kg·m−3)	7854 (kg·m−3)

.

Regarding cavitation, the Rayleigh-Plesset model is utilized [13]; vapour pressure is calculated following the Antoine equation (Equation (6)) [13].

logp = A_a − B_a/(C_a + T_f)

(6)

where A_a = 10.6751275622054, B_a = 2764.82814496125 and C_a = 24.0334359061956.

The Reynolds number is defined based on the rotor velocity and the minimum film thickness, H_min. For the thrust bearing, the rotor circumferential velocity U = ωD_m/2 is taken as the reference velocity, where D_m is the bearing mean diameter. As fluid viscosity decreases due to heating and shear thinning, a local value of the Reynolds number can also be considered; in the present study, a maximum value of about 340, accounting for 250 kRPM, has been obtained, therefore the flow in the lubricant domain is laminar for all studied cases.

2.2.1. Mesh Characteristics

Appropriate unstructured meshes of the fluid and the solid domains of the systems have been generated, involving approximately 4 × 10⁵ and 7 × 10⁵ cells, respectively. In the fluid film region of the tapered-land bearing, a minimum of 20 cell layers in the cross-flow direction (along film thickness) has been used, whereas in the pocket bearing model, a minimum of 40 cell layers in the cross flow direction has been used (20 layers have been used in the pocket region). In Figure 5 and Figure 6, the meshes can be visualized for both studied geometries. A mesh dependence study has been conducted.

2.2.2. Boundary Conditions

All walls are considered impermeable, and the no-slip condition is applied. The bearing rotor of the thrust bearing is rotating at a constant angular velocity, ω, giving a circumferential local velocity U = ω·r, where r is the local radius; rotational speed of the bearings varies from 50 kRPM to 250 kRPM. The inner fluid surface of the fluid domain (see Figure 6), is considered to be an opening, allowing flow in both directions. For the inner surface of the lubricant, a boundary pressure of 4 bar is considered. There, the feeding oil temperature is assumed to be constant at 150 °C, being a typical value of temperature of a highly loaded automotive engine. The outer fluid surface is considered as a pressure outlet, with a constant value of 0.0 MPa relative to atmospheric; a Neumann boundary condition is considered for the velocity and temperature, while no inflow is permitted. Rotational periodicity is considered for the inflow-outflow sides of the fluid and solid domains. This boundary, applied at the fluid domain accounts for hot-oil-carry-over between consecutive pads. At the fluid-solid interfaces, continuity of temperature and heat flux is implemented. In

Table 4. Thermal boundary conditions of the computational model.

Collar
Top surface	Heat transfer coeff: kair/(15·r)·Re2/3·Pr1/3, Tamb = 100 °C
Outer surface	Heat transfer coeff: kair/(15·r)·Re2/3·Pr1/3, Tamb = 100 °C
Bottom	Fluid-Solid interface: Continuity of heat flux and temperature
Inner surface	Heat transfer coeff: 1000 W/(m2·K),Tamb = 100 °C
Sides	Periodic Conditions
Pad
Top	Fluid-Solid interface: Continuity of heat flux and temperature
Bottom/Inner surface	Heat transfer coeff: 100 W/(m2·K), Tamb = 50 °C
Outer surface	Heat transfer coeff: 300 W/(m2·K), Tamb = 100 °C
Sides	Periodic Conditions
Fluid Domain
Inlet	Rotational periodicity (hot-oil carry-over taken into account)
Outer surface	Outlet: zero relative pressure
Sides	Periodic Conditions

Nomenclature: r: Rotor radius; Re: Local value of Reynolds number; Pr: Local value of Prandtl number, k_air: Specific heat capacity of air.

, all thermal boundary conditions of the model surfaces are identified. Operating conditions of the reference tapered-land bearing design are presented in

Table 5. Operating conditions of the reference tapered-land bearing.

Operating Conditions (Extreme)
Lubricating oil	5W30
Oil feed temperature	150 °C
Ambient temperature	100 °C
Oil feed pressure	4 bar
Rotational speed	200 kRPM

.

2.3. Optimization Procedure

The principal performance indices of a thrust bearing are load carrying capacity and friction coefficient. To optimize the performance of a thrust bearing, maximization of load carrying capacity will lead to larger film thickness for a given load (therefore less bearing wear and better performance in transient loads/impact loads), or to smaller bearing dimensions for a given value of minimum film thickness, which results in reduced friction power losses. Furthermore, minimization of the friction coefficient will contribute to reduced power losses. In the present study, two multi-objective optimization problems have been formulated:

Optimization Problem 1:	Optimization Problem 2:
Objective functions:	Objective functions:
(a) maximization of load capacity	(a) maximization of minimum film thickness
(b) minimization of friction coefficient	(b) minimization of friction coefficient
Minimum film thickness is considered constant.	Thrust load is considered constant.

3. Tapered-Land Geometry Optimization

3.1. Optimization Problem Setup

The geometric parameters used for the optimization of the tapered-land bearing are (a) the extent of the tapered part of the bearing as percentage of the length, and (b) the maximum taper depth in microns. Here, only the results of the first optimization problem are presented, since the second optimization problem did not demonstrate any significant improvements in terms of bearing performance.

3.2. Optimization Results

The present optimization of the tapered-land bearing geometry, aimed at minimization of power loss and maximization of load carrying capacity, for constant minimum film thickness, rotational speed of 200 kRPM and oil inflow temperature of 150 °C. In Figure 7a, the Pareto front of the present optimization is presented. In terms of power loss, there has been a mild improvement in the optimized geometries in relation to the reference case. Two optimal points on the Pareto front have been selected. Both designs exhibit values of load carrying capacity slightly higher than that of the reference case, followed by a reduction in friction power losses, ranging between 5% and 6%. In Figure 7b, the friction coefficient of the selected optimal designs can be visualised in the range between 50 and 250 kRPM, in comparison to that of the reference case. Further, in Figure 8, additional bearing performance indices (power loss, maximum temperature, maximum pressure) of the selected optimal designs are presented over the same RPM range. Based on the present results, power loss is shown to exhibit a substantial reduction, being higher than 10% at values of rotational speed less that 100 kRPM. Pressure and temperature distributions (depicted in Figure 9) present similar characteristics, due to the same principal geometric properties of the lubrication domain. In

Table 6. Operating conditions and performance indices of the optimal tapered-land designs, in comparison with the reference design, for constant value of minimum film thickness.

	Optimal Tapered-Land Design 1	Optimal Tapered-Land Design 2
Rotational Speed (kRPM)	200	200
Thrust Load difference (%)	+1.2	+1
Power Loss difference (%)	−7.35	−7.63
Maximum Temperature difference (K)	−10.47	−10.51
Maximum Pressure (%)	−0.6	−0.3

, a comparison between the performance indices of the two optimal tapered-land designs is shown for operation at 200 kRPM.

4. Curved Pocket Geometry Optimization

4.1. Optimization Problem Setup

Regarding the pocket geometry optimization, two optimization problems have been formulated and solved:

• Maximization of load capacity and minimization of power loss for given operating conditions (constant minimum film thickness, rotational speed of 200 kRPM, oil inflow temperature of 150 °C)
• Maximization of minimum film thickness and minimization of power loss for given operating conditions (thrust load, rotational speed of 200 kRPM, oil inflow temperature of 150 °C). Thrust load is set to the value obtained by the reference tapered-land design.

4.2. Optimization Results

The design variables of the pocket geometry optimization problems are the pocket extent, width, depth and curvature, as well as the oil inlet pocket extent and depth. As presented in Figure 10 and Figure 11, two Pareto fronts have been generated, one for each optimization problem.

Regarding the Pareto front of Figure 10: A substantial improvement of load carrying capacity is noticed. In terms of power loss, a minor increase is observed for the majority of the optimal designs. It should be noted that load carrying capacity improvement for a given minimum film thickness is equivalent to an increased minimum film thickness for a given working load, or to the possibility of the reduction of the thrust bearing external diameter, which can effectively reduce the power losses of the bearing. Two optimal designs of this Pareto front have been selected for further processing, which exhibit load carrying capacities substantially higher than that of the reference design (of the order of 60%) and slightly increased power loss (in the range of 4% to 6%).

Regarding the Pareto front of Figure 11: All optimal designs have shown a significant improvement in both minimum film thickness and power loss. One optimized design has been selected for further processing.

In Figure 12, bearing performance indices (power loss, maximum temperature, maximum pressure) of the selected optimal designs are presented in the range between 50 and 250 kRPM, in comparison to those of the reference tapered-land bearing design. Pressure and temperature distribution of the optimal pocket bearing designs (depicted in Figure 13) present similar distributions, due to the same principal geometric properties of the lubrication domain. Maximum pressure is observed at the pocket end region, whereas the smoother temperature distribution in the oil domain leads to larger areas of low viscosity oil, which substantially aids in enhancing pressure build-up.

In Table 6, the geometric parameters of the selected optimal designs are presented, followed by the comparison of operating and performance indices between the two optimal pocket designs and the reference tapered-land design in

Table 7. Operating conditions and performance indices of optimal pocket bearing designs, in comparison with the reference tapered-land bearing.

Optimal Designs (200 kRPM, Constant Load ± 2%)
Compared parameters	Optimal Design 1	Optimal Design 2	Optimal Design 3
Difference in Minimum Film Thickness [%]	+39.3%	+35%	+37%
Difference in Power Loss [%]	−10.63%	−10.62%	−10.24%
Difference in Maximum Temperature [K]	−17.35	−15.80	−15.92
Difference in Maximum Pressure [%]	−31.15%	−22.91%	−24.26%

.

4.3. Effect of Shear Thinning on Bearing Performance

In the present CFD simulations, the Cross equation has been used to describe the shear-rate influence on lubricant viscosity (see Section 2.2). Here, additional simulations have been performed for quantifying the effect of shear thinning on the principal performance indices of the bearing. In particular, in Figure 14, bearing performance indices (thrust load, friction torque, maximum pressure and power loss) are plotted against rotational speed for the pocket bearing design OPD 1 (Optimal Pocket Design 1). The blue dotted curves correspond to calculations utilizing the Cross equation for shear-rate influence on viscosity, whereas the red dotted curves correspond to calculations without considering the Cross equation. The results demonstrate that shear thinning substantially affects bearing performance, mostly at high values of rotational speed. The overestimation of thrust load and friction torque when shear thinning is not considered may be above 40% at values of rotational speed of 250 kRPM. Therefore, detailed numerical simulations for predicting bearing performance, taking into consideration shear thinning of the lubricant, are imperative in the design stage for obtaining accurate results.

4.4. Effect of Cavitation on Bearing Performance

In the present work, the Rayleigh-Plesset model has been used to predict cavitation occurrence in the lubricant domain (see details in Section 2.2). In Figure 15, contours of oil pressure, temperature and oil volume fraction are plotted against rotational speed for the pocket bearing design OPD 1. It can be observed that the probability of cavitation occurrence in the interior of the lubricant domain is very small, throughout the rotational speed of interest. At high values of rotational speed, a small cavitating region is observed at the outer bearing diameter, in the oil mixing pocket region, due to high values of lubricant temperature being present. However, the extent of the cavitation region is limited, and its effect on the pressure build-up of the bearing is negligible.

4.5. Parametric Study for Optimal Pocket Depth

In Figure 16, the effect of pocket depth on bearing load capacity for given value of minimum film thickness is presented. Two different CFD modeling approaches have been utilized, namely a thermohydrodynamic approach, accounting for viscosity variations in the lubricant domain, and an isothermal approach, where lubricant viscosity is assumed constant. In the latter case, the fixed value of viscosity is selected appropriately, so as to yield equal thrust load, as that of the THD model. For both models, a parametric analysis is performed to identify the effect of pocket depth on bearing load capacity. For the parametric analysis, the geometric parameters of the optimal pocket bearing design OPD 1 have been utilized. The results of the parametric analysis, presented in Figure 16, demonstrate that for isothermal conditions, the optimal ratio of pocket depth to minimum film thickness attains a value of 4.17, whereas the corresponding optimal ratio in THD conditions is substantially higher, attaining a value of 5. The observed behaviour may be explained based on considerations of optimum pocket geometry and of heat storage capacity of the lubricant in THD conditions. In particular, at isothermal conditions, an optimum pocket depth to minimum film thickness ratio corresponds to the value where pressure build-up is maximized. The behaviour of the bearing is similar to that of a Rayleigh step bearing. In THD conditions, lubricant viscosity decreases in the flow direction due to lubricant shear stress and heat dissipation. A smaller pocket will lead to better pressure build-up, however, the total lubricant mass in the pocket will be less, yielding increased temperature for given dissipated heat. If pocket depth is increased, heat capacity of the lubricant in the pocket region is increased, therefore temperature increase is milder, leading to higher values of lubricant viscosity. Therefore, optimum pocket depth may be evaluated as an interplay between a geometrically optimal step bearing, and a sufficiently large pocket volume for reducing the effect of lubricant heating.

Further, the present bearing design is characterized by very small-size, high values of rotational speed and very low values of film thickness. The larger pocket depth identified in this work, in comparison to that corresponding to conventional pocket bearing designs can be further attributed: (a) to the presence of substantial centrifugal forces of the present bearing, not considered in the Reynolds equation typically used in relevant studies; centrifugal fluid forces increase lubricant outflow rates at the outer bearing radius, requiring larger bulk amount of lubricant for optimal operation, (b) to the small width of the bearing pad, in comparison to length (small width to length ratio), which leads to rapid pressure drop at the inner and outer radii of the pad, and (c) to the lack of a fluid mixing groove before each pad of the present design, which leads to hot fluid mixing with cold fluid within the pocket domain. Thus, the optimizer, as the optimization process develops, favors values of the design variables which compensate for the above phenomena, concluding with optimal designs which are characterized by substantially larger pocket depth than that expected. Based on the present results, it can be concluded that detailed numerical simulations for predicting bearing performance, taking into consideration thermohydrodynamic behaviour of the lubricant and solid bearing parts, should be utilized in the design stage for obtaining accurate results. Bearing design based on the solution of Reynolds equation, or based on the assumption of isothermal conditions will yield designs that will perform sub-optimally under the actual operating conditions.

5. Conclusions

The present study was concerned with the design optimization of the thrust bearing of an automotive turbocharger. The reference design is a small footprint, four-pad, grooveless, tapered-land thrust bearing design, with a lip at the outer radius of the bearing pad, in order to minimise side oil leakage. The goals of the present study were the geometry optimization of (i) a tapered-land bearing design, similar to the reference one, and (ii) a pocket bearing design with the same principal dimensions. Optimization has been carried out for a rotational speed of 200 kRPM. The optimization goals were (a) to minimize power losses and maximize minimum oil film thickness for given load capacity, and (b) to minimize friction coefficient and maximize load capacity for given minimum oil film thickness. Optimization has been performed with an in-house optimizer, which was coupled to ANSYS CFX code. The Pareto fronts of the optimization problems have been obtained, and different optimum designs have been identified. The optimum bearing designs have been further studied by means of a parametric analysis for different values of rotational speed (50 kRPM to 250 kRPM).

Regarding the tapered-land bearing, two optimal designs have been selected. Optimal design 1 exhibits the best performance for operation at 200 kRPM. In particular, for constant value of oil minimum film thickness, power loss has shown a decreasing trend by 7.5%, in comparison to the reference design. Maximum pressure has shown to exhibit a moderate decrease (approximately 6% at high values of rotational speed), in comparison to the reference design, whereas maximum temperature has exhibited a negligible decrease (approximately 1 °C at high values of rotational speed). The identified optimal taper depths are substantially higher than those of common designs, attributed to the peculiarities of the present design, characterized by very small-size, high values of rotational speed and very low values of film thickness, giving rise to high values of operating oil temperature.

Regarding the pocket bearing, three optimal designs have been identified. Optimal design 1 exhibits the best performance, in operation at 200 kRPM for a constant Load. In particular, minimum oil film thickness is increased by 40%, whereas power loss is decreased by 12%, in comparison to the reference geometry design. Maximum pressure exhibits a substantial decrease (approximately 30% at high values of rotational speed), in comparison to the reference design. Maximum temperature also exhibits a substantial decrease (reaching approximately 16 °C at high values of rotational speed). A parametric analysis of the effect of pocket depth on bearing performance reveals that pocket depths of the order of five times the value of film thickness are required for optimal bearing performance.

Based on the present results, the following conclusions can be drawn:

(a)

Properly designed pocket bearings may aid in substantially improving the performance of turbocharger thrust bearings, by operation at higher oil film thickness and substantially reduced power losses. In the studied regime, the pocket extent should be approximately 80%, whereas the pocket depth should be approximately 4–6 times the minimum film thickness. A relatively deep oil entrance pocket is essential for providing fresh oil and minimizing the effect of hot-oil-carry-over. In all cases, the pocket curvature should be mild.

(b)

Optimal parameters of pocket bearing designs may be different in different applications, being mostly affected by the bearing size, thrust load and environment conditions. Therefore, detailed calculations should be performed to verify optimum performance in the design stage.

(c)

In thrust bearing applications, high loads, low values of minimum film thickness and high values of temperature give rise, on one hand to shear thinning, which may affect substantially lubricant viscosity, and on the other hand to cavitation, which may reduce bearing load capacity, degrade gradually the lubricating oil properties and increase the wear rate of the system. Therefore, detailed numerical simulations for predicting bearing performance are imperative in the design stage.