7.1. Steady Load, Numerical Error, and Perturbed Reynolds Equation Verification
Prior to examining the dynamic coefficients evaluated using the transient Reynolds equation or CFD with a moving boundary, the steady-state load predicted for the linear slider bearing is compared between the Reynolds equation and CFD. Additionally, discretization and iterative convergence errors are quantified as well as the effect of advective inertia under steady operating conditions.
As a final precursor to evaluation of dynamic coefficients using transient Reynolds and transient CFD with a moving boundary, the stiffness and damping coefficients are predicted using the perturbed Reynolds equation and verified against previously published results [
13]. The perturbed Reynolds equation results will serve as a basis for comparison for the linear slider bearing results using the proposed method of dynamic coefficient computation in conjunction with transient Reynolds and CFD with moving boundaries.
7.1.1. Linear Slider Bearing, Steady Numerical Error and Advective Inertia Effects
For the infinitely long, linear slider bearing, the steady Reynolds equation can be solved analytically for the dimensionless, steady-state load per unit length (
, where
w is the dimensional load per unit length) the result given in Equation (
29) as a function of the taper ratio (
) [
31] is
The steady-state load predicted by a finite difference numerical solution of the steady-state Reynolds equation has a 0.05% error relative to the Equation (
29) (for a taper ratio
). The small error validates the finite-difference discretization and iterative schemes (Gauss–Seidel) used to numerically solve the steady-state Reynolds equation. Note that iterative convergence is achieved when the normalized residual for pressure (normalized sum of values at all the grid points) is less than 1 × 10
. The steady-state load resulting from the CFD solution of the Stokes formulation has a 1% error relative to the exact solution, when an evenly spaced grid was used (15 cells across the lubricant film, and 221 cells in the sliding direction).
In order to estimate the discretization errors associated with steady-state load, the grid convergence index (GCI) detailed in Celik et al. [
32] is applied. At its core, the GCI is a Richardson Extrapolation method, a widely accepted method for reporting discretization errors in CFD. Application of the GCI requires numerical computations on three successively refined grids, which will be denoted “coarse”, “nominal”, and “fine” grids. The discretization error associated with the steady-state load can then be computed for the nominal and fine grids.
Reynolds equation’s numerical solution, grids of 25, 50, and 100 evenly spaced points (in the sliding direction) result in discretization errors in the steady-state load of 0.07% and 0.02% on the nominal and fine grids, respectively.
For the Stokes CFD solution, evenly spaced grids are examined. The “coarse” grid has 10 cells in the y-direction and 147 cells in the x-direction. The “nominal” grid has 15 and 221 cells in the y- and x-directions, respectively. The “fine” grid has 20 and 294 cells in the y- and x-directions, respectively. Discretization errors in the steady-state load of 1.3 and 0.9 percent on the nominal and fine grids are respectively found. The Reynolds equation solution exhibits an order of convergence of 2.07 consistent with the second-order discretization scheme. The apparent order of convergence of the Stokes CFD solution is 1.66. Overall, the nominal grids for the Reynolds equation and Stokes CFD solutions exhibit discretization errors of approximately 1% or less, warranting their usage and providing confidence that differences between CFD and Reynolds equation-based results exceeding 1% are not attributable to discretization errors associated with the respective methods.
For the nominal geometric dimensions and operating conditions, the reduced sliding Reynolds number
(
) results in steady load differences predicted using NSE (with advective inertia) and Stokes equations (without advective inertia) of less than 1%. These results are consistent with the assertion that advective inertia effects can be neglected for
, Szeri [
21].
7.1.2. Pure Squeeze Motion Transient Numerical Error
Mesh motion can introduce additional numerical errors with the CFD results that are not captured in the GCI presented above. Therefore, the GCI is re-evaluated for flow between parallel plates subject to pure squeeze, harmonic motion on the three successively refined grids described above. The transient Stokes CFD solution is obtained for each grid and the predicted damping coefficients provide the quantitative metric for the GCI computation.
The dimensionless damping coefficients (per unit length) predicted (using the frequency domain method) on the “coarse”, “nominal”, and “fine” grids are 0.1729, 0.1746, and 0.1751, respectively. The “fine” and “nominal” GCI corresponding to the damping coefficient are 0.3% and 0.7%, respectively. The apparent order of convergence is 2.5. Proceeding with the nominal grid, the discretization errors for the transient cases (which are compounded by the presence of mesh motion) are assumed to remain less than 1% for integrated quantities such as stiffness coefficient, damping coefficient, and added mass coefficient.
The effect of local grid density on the damping coefficient was also assessed for the pure squeeze motion between parallel plates. If the “nominal” grid is used but the 15 cells distributed across the thin fluid film are packed more closely to the oscillating boundary, the resulting damping coefficient is 0.1724. The relative error in damping coefficient due resulting from an evenly spaced grid rather than a locally refined grid near the oscillating boundary is 1.3%. For the locally refined grid, the ratio of the height of the cell adjacent to the osciallating boundary to the height of the cell adjacent to the stationary boundary is 0.1.
7.1.3. Linear Slider Bearing, Perturbed Reynolds Equation Verification
The stiffness and damping coefficients predicted using the perturbed Reynolds equation are verified by comparison with the results of Lin and Hung [
13] as well as our analytic solution. In
Figure 2, the dimensionless stiffness and damping coefficients are plotted over a range of taper ratios. The numerical solution of the perturbed Reynolds equation from the present work matches the analytic solution and confirms that discretization and iterative convergence errors are sufficiently small. The perturbed Reynolds equation results from the present work are comparable with [
13] (which were also predicted using the perturbed Reynolds equation). Discrepancies in
K and
D are attributable to the method by which the results of Lin and Hung were extracted from the original paper [
13].
K and
D were extracted from a digitized version of a figure in the original paper and then scaled by a factor of six (to reconcile differences in non-dimensionalization).
7.2. Transient, Pure Squeeze Motion between Infinite Parallel Plates
As the sliding velocity of the linear slider bearing approaches zero () and the taper ratio approaches unity (), the flow within the infinitely long, linear slider bearing becomes that of flow between infinitely long, parallel plates. When the lower wall (“movingWall”) of the bearing is given a harmonic displacement normal to the sliding direction (y-direction), the flow becomes pure squeeze motion between infinitely long parallel plates. This type of flow may be viewed as the simplest type of transient flow that develops within a linear slider bearing, warranting it as the first test case to evaluate the dynamic coefficients using transient Reynolds and transient CFD with a moving boundary.
The same form of the dimensionless dynamic coefficients is applied to pure squeeze motion between parallel plates as to the linear slider bearing, while, for pure squeeze motion, the sliding velocity prescribed in the Reynolds equation and CFD models is zero, and a sliding velocity (other than zero) is nonetheless required as part of the non-dimensionalization of the dynamic coefficients. For pure squeeze motion between parallel plates, a sliding velocity (m s) (sliding velocity of linear bearing) is used within the non-dimensionalization of the dynamic coefficients to maintain consistency.
For pure squeeze motion between infinitely long, parallel plates, the transient Reynolds equation can be solved analytically and results in a dimensionless load given by Equation (
30) San Andrés [
31]:
If the dimensionless film thickness
is substituted into Equation (
30), the result is Equation (
31):
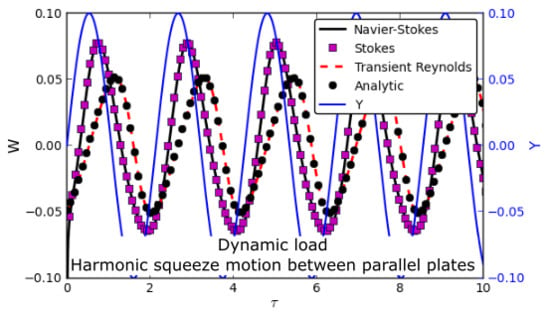
The dynamic load predicted by the transient Reynolds equation and transient CFD with a moving boundary are both compared in
Figure 3 against the analytic solution for the dynamic load offered by Equation (
31).
In
Figure 3, the numerical solution of the transient Reynolds equation (red dashed line) lies on top of the analytic solution given by Equation (
31) (black solid circle). Using CFD with a moving boundary (Stokes and Navier–Stokes), the transient load does not match the analytic solution. While solutions of the Navier–Stokes equations (with inertia, black solid line) and the Stokes equations (without inertia, magenta square) result in dynamic loads comparable with each other, both differ in both magnitude and phase from the analytic solution. The dynamic load predicted using CFD with a moving boundary has a larger amplitude and lags the analytic, dynamic load. Since the CFD solution of the NSE and Stokes equations result in the same dynamic load, advective inertia effects for
can be considered negligible.
The dynamic loads in
Figure 3 can be used to estimate the dynamic properties of the squeeze film between the parallel plates. The analytic solution for the dynamic load results in zero stiffness and a dimensionless damping coefficient per unit length,
. The time and frequency domain estimates based on the dynamic load from the transient Reynolds equation also result in zero stiffness and the same damping coefficient,
. However, the dynamic load predicted by CFD with a moving boundary results in stiffness and damping coefficients,
and
, respectively, using both the time and frequency domain estimates. The time and frequency domain methods for estimating the dynamic coefficients described in the present work are verified through the accuracy of the damping coefficient predicted. There is negligible error when using the dynamic load from transient Reynolds to determine the damping coefficient. Additionally, the error is only
% when dynamic load from CFD with a moving boundary is used to estimate the coefficients.
The non-zero value for K is not physically relevant. This is clear if we evaluate the change in force generated by the flow between parallel plates when the film thickness is subject to a small, finite displacement, . If the flow is steady, and the film thickness is , the load is zero, . If the film thickness is increased slightly, , the steady load will again be zero, . The stiffness can then be approximated as . In the case of pure squeeze motion between parallel plates, the stiffness K must be zero. A non-zero, non-physical value for K results because the dynamic model of the bearing is not correct for transient CFD with temporal inertia effects. In reality, it is not K that is being computed but the dynamic stiffness, . The temporal inertial effects must be captured through the addition of an added mass coefficient to the dynamic model.
The increased amplitude and phase lag in the dynamic load predicted by CFD with a moving boundary and the corresponding non-physical
K result from temporal inertia effects. Temporal inertia effects arise due to the presence of the transient, or temporal inertial terms,
, in the linear momentum conservation equations. Temporal inertia is present within the linear momentum equations of both the transient Navier–Stokes and transient Stokes equations—Equations (
4) and (
5), respectively. In pure squeeze flow, the oscillating lower boundary of the domain pushes and pulls on the fluid, causing it to accelerate and causing the acceleration,
, within the linear momentum equation in the
y-direction “activate”. Through the services of the continuity equation for the incompressible flow, the temporal inertia term in the
y-direction activates the temporal inertia term in the
x-direction of linear momentum,
. As an example, consider the squeezing of an incompressible column of fluid situated between the parallel plates. As the fluid is squeezed, the column of fluid perpendicular to the direction of squeeze will have to expand in the
x-direction in order to preserve volumetric and mass continuity. The phenomenon is akin to the Poisson ratio and the transverse contraction strain resulting from logitudinal extension strain. In the linear momentum equation in the
x-direction, the additional fluid acceleration
has to be balanced by an increase in the pressure gradient
and subsequently an increase in the pressure and normal load (integrated pressure). By contrast, in the steady-state form of the linear momentum equation in the
x-direction, the pressure gradient balances only the viscous shear.
One can therefore conclude that the net effect of the temporal inertia term on the flow between parallel plates (and by extension the flow in a linear slider bearing or any other bearing subject to the same effect) is to increase the magnitude of the dynamic load and change its phase. To account for the temporal inertia, it is necessary to modify the dynamic model of the slider bearing behavior. In addition to a spring and damper, a dimensionless added mass coefficient per unit length,
(where
m is the dimensional added mass per unit length), must be incorporated into the linear dynamic model of the total, transient, dimensionless bearing load per unit length, resulting in Equation (
32):
Both the time domain and frequency domain estimates of the linearized dynamic coefficients (
K,
D,
M) can be modified to include the added mass coefficient. The time domain estimate can be made by solving the overdetermined system, Equation (
33), for the bearing parameters
K,
D, and
M:
In the frequency domain, Equation (
33) leads to the frequency response function given by Equation (
34):
The particular form of the frequency response function given by Equation (
34) is also known as the dynamic stiffness and consists of both real and imaginary components. The imaginary component can be used to determine the damping coefficients as introduced previously:
It is noteworthy, however, that the real component contains both the static stiffness and the added mass of the fluid within the bearing:
Equation (
32) applies only to the dynamic load predicted by CFD with a moving boundary. The classical Reynolds equation (perturbed form or transient) has by initial assumption excluded temporal inertia as part of its derivation. As a result, there are no added mass effects within the load resulting from Reynolds equation and for that reason alone a spring-damper model should be used to model the bearing dynamic behavior in the present work. Added mass coefficients (inertia parameters) would be required if inertia effects were retained within the Reynolds equation as in Dousti [
33].
Tichy and Modest [
34] previously investigated discrepancies between CFD and Reynolds equation results for squeeze film flow between parallel and inclined plates. As in the present work, Tichy and Modest identified fluid inertia as the source of increased load amplitude predicted by CFD. However, the authors did not attempt to capture temporal inertia effects through an added mass coefficient within the dynamic model of the bearing.
For flow between parallel plates, the stiffness, K is zero and the added mass coefficient resulting from the temporal inertia of the fluid can be solved for directly. Using the dynamic models of the slider bearing described above and modified to account for temporal inertia effects, new estimates of the dynamic properties of squeeze flow between parallel plates using CFD with a moving boundary are made. The damping coefficient remains the same, (% larger than transient Reynolds), and the dimensionless, added mass coefficients per unit length predicted using time and frequency domain methods are and , respectively. As the Reynolds equation does not account for temporal inertia, the resulting dynamic load exhibits no added mass effects and the dynamic response of the fluid film subject to boundary oscillation is very different from that predicted by CFD.
The need to include an added mass coefficient to account for temporal inertia effects within the CFD-predicted loads is rather surprising. The reduced squeeze Reynolds number, , is comparatively small when viewed alongside the reduced sliding Reynolds number . While the present work supported the claim that advective inertia effects are negligible for , it seems that a different, and much smaller threshold reduced Reynolds number exists. The determination of a threshold value of is reserved for a subsequent paper.
7.3. Transient, Infinitely Long Linear Slider Bearing with Oscillating Boundary
The dynamic load of an infinitely long, linear slider bearing subject to harmonic oscillation perpendicular to the direction of sliding (harmonic squeeze motion) is plotted in
Figure 4. The linear slider bearing has a taper ratio
and is subject to a sliding velocity
(m s
), in addition to the motion of the oscillating boundary that oscillates at a frequency of 141 (rad s
) and with an amplitude equal to 10% of
.
As with the pure squeeze motion between parallel plates, in
Figure 4, the dynamic load predicted by CFD with a moving boundary is markedly different than the dynamic load predicted by the transient Reynolds equation. Both the amplitude and the phase of the predicted dynamic loads differ, owing to the presence of temporal inertia within the CFD results. The dimensionless stiffness and damping coefficients predicted from the transient Reynolds force in
Figure 4 are 0.056 and 0.053, respectively, using the time domain estimate. The frequency domain estimates of
K and
D from the transient Reynolds equation are 0.055 and 0.053, respectively. The analytic solution of the Reynolds equation predicts
and
. Differences between the transient Reynolds equation and analytic results for
K and
D are within errors associated with discretization and iterative convergence errors of the transient Reynolds equation numerical solution. In fact, the coincidence of the results is very good and reassuring in regard to the correctness of the methodology.
For the linear slider bearing dynamic model comprised only of a spring and damper; using the time domain estimation method, the dynamic force from CFD with a moving boundary (
Figure 3) results in
and
. Evaluation of the stiffness and damping using the frequency domain method yields almost identical values of
and
, respectively. The negative direct stiffness coefficient is non-physical and results from the absence of an added mass coefficient within the dynamic model of the slider bearing. If an added mass coefficient is introduced in the dynamic model, the negative stiffness would make more sense since it would represent a component of the dynamic stiffness,
, rather than just a static stiffness
K. Note that, unlike for the pure squeeze motion between parallel plates, it is not possible to separate
K and
M from
by just using a single forced oscillation frequency
. It would be necessary to fit the stiffness and mass parameters,
K and
M, respectively, over a range of excitation frequencies
. The determination of
K and
M from the quantity
is the subject of a subsequent paper. However, it is noteworthy to mention that a preliminary investigation into resolving
K and
M separately from CFD with a moving boundary, determined that both dynamic parameters exhibit some excitation frequency dependence not predicted by Reynolds equation.
Table 1 summarizes
K,
D, and
for the linear slider bearing at various taper ratios predicted by our analytic solution, as well as by the proposed frequency domain estimation method using the dynamic forces obtain through both the transient Reynolds equation and transient CFD with a moving boundary.
K and
D predicted by our analytic solution and transient Reynolds equation match exactly for higher taper ratios, while a 10%, difference in
K manifests itself at the lowest taper ratio,
.
For the CFD with a moving boundary, it was possible to directly compare the damping coefficients with our analytic and transient Reynolds equation predicted results. Generally, CFD with a moving boundary over-predicted the damping coefficient when compared to our analytic solution and transient Reynolds equation. For , CFD predicts a 6% higher D, while, for , the over-prediction rises to 104%. We believe that the CFD model predicts higher values than our analytic solution due to the increased role played by additional viscous terms present in the CFD model (Stokes equations vs. Reynolds equation). The additional viscous terms may increase energy dissipation results in higher values of D predicted by CFD with a moving boundary. In a subsequent paper, numerical errors will be directly quantified for the transient CFD with a moving boundary, and the role of additional viscous terms within the governing equations will be investigated.