Development of a Constitutive Model for Friction in Bulk Metal Forming
Abstract
:1. Introduction
2. Materials and Methods
2.1. Test Samples
2.2. Pin-on-Disk Tribometer
2.3. Lubricant System
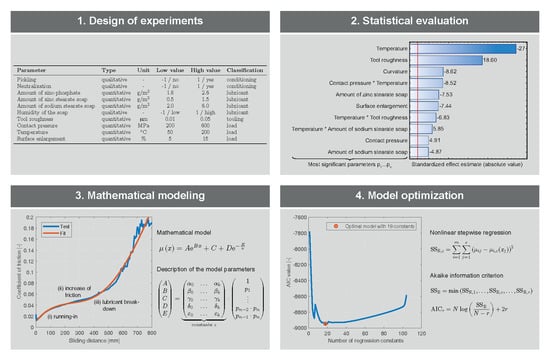
2.4. Design of Experiments
3. Results and Discussion
- Perform the experiments based on the randomized experimental design.
- Identifiy the friction influencing factors by statistical evaluation.
- Determine a mathematical function that can describe the measured friction curves.
- Build a global friction model as a function of the friction influencing factors.
- Optimize and simplify the friction model by stepwise nonlinear regression.
3.1. Friction Curves
3.2. Friction Influencing Parameters
- temperature
- tool roughness
- amount of zinc stearate soap
- surface enlargement
- contact pressure
- amount of sodium stearate soap
3.3. Friction Modeling
3.4. Friction Model for Tube Drawing
4. Conclusions
- Design of experiments: A two-level screening plan was used for efficient and systematic testing of friction under varying contact conditions. To identify possible nonlinearities, center point experiments were applied. The experiments were conducted on a pin-on-disk tribometer based on a randomized experimental design.
- Statistical evaluation: Key parameters that mainly affect the coefficient of friction were identified by statistical evaluation of the measured friction curves using the design of experiments approach.
- Mathematical modeling: Based on the shapes of the measured friction curves, a mathematical model was selected. The model coefficients were described as a function of the key parameters that mainly affect the coefficient of friction. This led to an initial friction model with a high number of regression constants, where over-fitting may be an issue.
- Optimization: An optimal friction model with less regression constants was obtained as a trade-off between model accuracy and complexity by using stepwise nonlinear regression and a modified version of the Akaike information criterion.
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Altan, T.; Vazquez, V. Numerical Process Simulation for Tool and Process Design in Bulk Metal Forming. CIRP Ann. 1996, 45, 599–615. [Google Scholar] [CrossRef]
- Tekkaya, A.E.; Martins, P.A.F. Accuracy, reliability and validity of finite element analysis in metal forming: A user’s perspective. Eng. Comput. 2009, 26, 1026–1055. [Google Scholar] [CrossRef]
- Bay, N.; Eriksen, M.; Tan, X.; Wibom, O. A friction model for cold forging of aluminum, steel and stainless steel provided with conversion coating and solid film lubricant. CIRP Ann. Manuf. Technol. 2011, 60, 303–306. [Google Scholar] [CrossRef]
- Wang, W.; Zhao, Y.; Wang, Z.; Hua, M.; Wei, X. A study on variable friction model in sheet metal forming with advanced high strength steels. Tribol. Int. 2016, 93, 17–28. [Google Scholar] [CrossRef]
- De Coulomb, C.A. Théorie des Machines Simples: En Ayant égard au Frottement de Leurs Parties et à la Roideur des Cordages; Bachelier: Paris, France, 1821. [Google Scholar]
- Amontons, G. De la resistance cause’e dans les machines. Memoire de l’Académie Royale des Sciences 1699, 2, 206–227. [Google Scholar]
- Bowden, F.P.; Tabor, D. Mechanism of metallic friction. Nature 1942, 150, 197–199. [Google Scholar] [CrossRef]
- Orowan, E. The Calculation of Roll Pressure in Hot and Cold Flat Rolling. Proc. Inst. Mech. Eng. 1943, 150, 140–167. [Google Scholar] [CrossRef]
- Shaw, M.C.; Ber, A.; Mamen, P.A. Friction characteristics of sliding surface undergoing plastic flow. Trans. ASME J.Basic Eng. 1960, 82, 342–346. [Google Scholar] [CrossRef]
- Schey, J.A. (Ed.) Metal Deformation Processes: Friction and Lubrication; Dekker: New York, NY, USA, 1970. [Google Scholar]
- Wanheim, T.; Bay, N. A Model for Friction in Metal Forming Processes. CIRP Ann. Manuf. Technol. 1978, 27, 189–194. [Google Scholar]
- Nielsen, C.V.; Bay, N. Review of friction modeling in metal forming processes. J. Mater. Proc. Technol. 2018, 255, 234–241. [Google Scholar] [CrossRef]
- Hashiguchi, K.; Ozaki, S. Constitutive equation for friction with transition from static to kinetic friction and recovery of static friction. Int. J. Plast. 2008, 24, 2102–2124. [Google Scholar] [CrossRef]
- Ozaki, S.; Ito, C.; Hashiguchi, K. Experimental verification of rate-dependent elastoplastic analogy friction model and its application to FE analysis. Tribol. Int. 2013, 64, 164–177. [Google Scholar] [CrossRef]
- Hol, J.; Cid Alfaro, M.V.; de Rooij, M.B.; Meinders, T. Advanced friction modeling for sheet metal forming. Wear 2012, 286–287, 66–78. [Google Scholar] [CrossRef]
- Hol, J.; Meinders, V.T.; Geijselaers, H.; van den Boogaard, A.H. Multi-scale friction modeling for sheet metal forming: The mixed lubrication regime. Tribol. Int. 2015, 85, 10–25. [Google Scholar] [CrossRef]
- Hol, J.; Meinders, V.T.; de Rooij, M.B.; van den Boogaard, A.H. Multi-scale friction modeling for sheet metal forming: The boundary lubrication regime. Tribol. Int. 2015, 81, 112–128. [Google Scholar] [CrossRef]
- Ludwig, M.; Stahlmann, J.; Groche, P. Advanced Friction Model for Cold Forging Processes. In Metal Forming; Wiley-VCH Verlag GmbH & Co.: Weinheim, Germany, 2012; pp. 1003–1006. [Google Scholar]
- Horwatitsch, D. Entwicklung eines Reibmodells für hohe Temperaturen und hohe Umformgrade: @Kassel Univ., 2012, Dissertation; Berichte zur Metallformgebung; Kassel University Press: Kassel, Germany, 2013. [Google Scholar]
- Tamai, Y.; Inazumi, T.; Manabe, K.I. FE forming analysis with nonlinear friction coefficient model considering contact pressure, sliding velocity and sliding length. J. Mater. Proc. Technol. 2016, 227, 161–168. [Google Scholar] [CrossRef]
- Rigaut, J.M.; Oudin, J.; Bricout, J.P.; Cabezon, J.; Ravalard, Y. A new friction test procedure for the improvement of drawing and similar processes. J. Mater. Proc. Technol. 1990, 21, 3–28. [Google Scholar] [CrossRef]
- Bay, N.; Wibom, O.; Nielsen, J.A. A New Friction and Lubrication Test for Cold Forging. CIRP Ann. Manuf. Technol. 1995, 44, 217–221. [Google Scholar] [CrossRef]
- Bay, N.; Olsson, D.D.; Andreasen, J.L. Lubricant test methods for sheet metal forming. Tribol. Int. 2008, 41, 844–853. [Google Scholar] [CrossRef]
- Groche, P.; Müller, C.; Stahlmann, J.; Zang, S. Mechanical conditions in bulk metal forming tribometers—Part one. Tribol. Int. 2013, 62, 223–231. [Google Scholar] [CrossRef]
- Groche, P.; Stahlmann, J.; Müller, C. Mechanical conditions in bulk metal forming tribometers—Part two. Tribol. Int. 2013, 66, 345–351. [Google Scholar] [CrossRef]
- Müller, C.; Groche, P. Tribological measurement in cold forging. Tribol. Schmier. 2014, 61, 28–37. [Google Scholar]
- Velkavrh, I.; Lüchinger, M.; Kern, K.; Klien, S.; Ausserer, F.; Voyer, J.; Diem, A.; Schreiner, M.; Tillmann, W. Using a standard pin-on-disc tribometer to analyse friction in a metal forming process. Tribol. Int. 2017, 114, 418–428. [Google Scholar] [CrossRef]
- Freeman, D.B. Phosphating and Metal Pre-Treatment: A Guide to Modern Processes and Practice; Woodhead-Faulkner: Cambridge, UK, 1986; Volume 1986. [Google Scholar]
- Adjerid, S.; Hivart, P.; Bricout, J.P. Some stressing and environmental parameters related to phosphate-stearate coating performance in cold forging of steel. Tribol. Lett. 1996, 2, 55–70. [Google Scholar] [CrossRef]
- Bricout, J.P.; Hivart, P.; Oudin, J.; Ravalard, Y. New testing procedure of zinc phosphate coatings involved in cold forging of cylindrical steel billets. J. Mater. Proc. Technol. 1990, 24, 3–12. [Google Scholar] [CrossRef]
- Hivart, P.; Bricout, J.P.; Oudin, J. New real-time test for prediction of zinc phosphate/stearate coatings breakdown: optimal stearate settling parameters for steel billets in cold forging. Tribol. Int. 1992, 25, 45–51. [Google Scholar] [CrossRef]
- Groche, P.; Zang, S.; Müller, C. Einfluss der Relativgeschwindigkeit auf tribologische Systeme der Kaltmassivumformung. Tribol. Schmier. 2014, 61, 26–32. [Google Scholar]
- Montgomery, D.C.; Runger, G.C.; Hubele, N.F. Engineering Statistics, 5th ed.; Wiley: Hoboken, NJ, USA, 2010. [Google Scholar]
- Akaike, H. A New Look at the Statistical Model Identification. IEEE Trans. Autom. Control 1974, 19, 716–723. [Google Scholar] [CrossRef]






| Parameter | Type | Unit | Low value | High value | Classification |
|---|---|---|---|---|---|
| Pickling | qualitative | - | −1/no | 1/yes | conditioning |
| Neutralization | qualitative | - | −1/no | 1/yes | conditioning |
| Amount of zinc-phosphate | quantitative | g/m | 1.8 | 2.6 | lubricant |
| Amount of zinc stearate soap | quantitative | g/m | 0.5 | 1.5 | lubricant |
| Amount of sodium stearate soap | quantitative | g/m | 2.0 | 6.0 | lubricant |
| Humidity of the soap | qualitative | - | −1/low | 1/high | lubricant |
| Tool roughness | quantitative | m | 0.01 | 0.05 | tooling |
| Contact pressure | quantitative | MPa | 200 | 600 | load |
| Temperature | quantitative | C | 50 | 200 | load |
| Surface enlargement | quantitative | % | 5 | 15 | load |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lüchinger, M.; Velkavrh, I.; Kern, K.; Baumgartner, M.; Klien, S.; Diem, A.; Schreiner, M.; Tillmann, W. Development of a Constitutive Model for Friction in Bulk Metal Forming. Lubricants 2018, 6, 42. https://doi.org/10.3390/lubricants6020042
Lüchinger M, Velkavrh I, Kern K, Baumgartner M, Klien S, Diem A, Schreiner M, Tillmann W. Development of a Constitutive Model for Friction in Bulk Metal Forming. Lubricants. 2018; 6(2):42. https://doi.org/10.3390/lubricants6020042
Chicago/Turabian StyleLüchinger, Marco, Igor Velkavrh, Kerstin Kern, Michael Baumgartner, Stefan Klien, Alexander Diem, Michael Schreiner, and Wolfgang Tillmann. 2018. "Development of a Constitutive Model for Friction in Bulk Metal Forming" Lubricants 6, no. 2: 42. https://doi.org/10.3390/lubricants6020042
APA StyleLüchinger, M., Velkavrh, I., Kern, K., Baumgartner, M., Klien, S., Diem, A., Schreiner, M., & Tillmann, W. (2018). Development of a Constitutive Model for Friction in Bulk Metal Forming. Lubricants, 6(2), 42. https://doi.org/10.3390/lubricants6020042