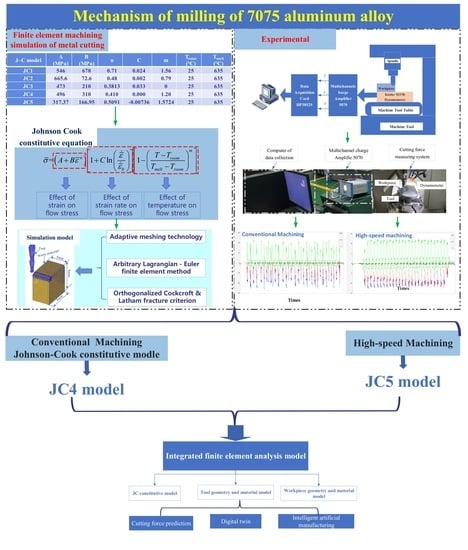
Research on Conventional and High-Speed Machining Cutting Force of 7075-T6 Aluminum Alloy Based on Finite Element Modeling and Simulation

Abstract

In current industrial practice, the finite element modeling of the metal cutting process is essential. In this paper, finite element analysis of conventional and high-speed cutting of 7075-T6 aluminum alloy is carried out. A finite element model of the 7075-T6 aluminum alloy was developed using the Johnson Cook instant on equation to investigate the milling behavior of the alloy under conventional and high-speed conditions. The cutting forces in the X-direction, Y-direction, and Z-direction were predicted analytically for five groups of different Johnson Cook models with different material constants, and the predicted results were compared with the experimentally determined cutting forces to investigate the influence of the Johnson Cook constitutive model parameters on the simulation of the cutting forces of the 7075-T6 aluminum alloy. The results showed that the constitutive model parameters are inconsistent for conventional and higher speed cutting conditions. Under conventional cutting conditions, the JC4 model predicts the material factor cutting forces in good agreement with the experimental results, while under high-speed cutting conditions, the JC5 model predicts the material factor cutting forces in good agreement with the experimental results, but that the finite element model has good applicability in predicting machining performance. Only the experimental data obtained by covering the real strain, strain rate and temperature range to determine the material constant of the Johnson Cook constitutive equation can accurately predict the cutting force in all directions.

1. Introduction

Aluminum alloys have long been favored in the aerospace industry, as well as transportation applications such as marine and automotive, and manufacturing and construction [1,2,3]. Because of its low density, good plasticity, corrosion resistance, heat-treatable characteristics, high strength-to-weight ratio, and machinability equivalent to various metals, 7075-T6 (Al-Zn-Mg-Cu) aluminum alloy is particularly appealing to manufacturers, engineers, and researchers in the applications listed above [4,5,6]. Moreover, many aspects of machining, chip formation, cutting forces, cutting temperatures, and surface integrity of machined products are affected by mechanical and thermal properties [7,8,9]. The material flow stress, which is influenced by strain, strain rate, and temperature, is one of the most crucial mechanical properties [10]. There is an increasing requirement to accurately anticipate material flow stress using numerical methodology or analytical approaches. Therefore, it is required to build a trustworthy FE model for the ordinary cutting speed regime and, notably, for high-speed machining, in order to maximize productivity and mechanical surface integrity in the machining of Al7075-T6. Knowledge of material constitutive behavior under these extreme loading circumstances is a must for effectively analyzing this process using numerical methods such as finite element analysis (FEA), and hence precise work material flow stress data must be employed.

In reality, work material flow stress, friction parameters between the tool and work material interfaces, the fracture criteria, and thermal parameters all play a role in the success and reliability of numerical models. Malea et al. [11] briefly presented the basic methodologies and techniques utilized in numerical modeling and simulation of machining by analyzing current studies. Melkote et al. [12] examined recent developments in constitutive and friction data and models for metal machining simulations, and introduced and analyzed phenomenological and physically-based constitutive models typically employed in machining simulations. Islam et al. [13] presented numerical simulations of metal cutting processes using Eulerian and Total Lagrangian Smoothed Particle Hydrodynamics. From an analysis of the literature above, the precise selection of these parameters is often seen as a crucial step if the objective is to predict cutting characteristics such as cutting forces, chip morphology and temperature fields.

Moreover, several research groups have sought to construct material constitutive equations and have proposed their own formulations by combining empirically-obtained data into a single equation. Johnson and Cook [14] created a constitutive equation that assumed the stress’s dependence on strain, strain rate, and temperature can be multiplicatively decomposed into three separate functions, each with five constants defined by experimental data for a given material. In order to simulate serrated chip formation, Calamaz et al. [15] proposed another modification of the J-C model for finite element simulations. The strain softening effect resulting from strain softening and temperature softening was introduced by this modification model. Jung et al. [16] developed a user-defined material model and incorporated the model into the Johnson−Cook constitutive relationship, and a gas-gun system experiment was used to investigate the behavior of 7075-T651 aluminum alloy plate in high-speed impact. Trimble et al. [17] evaluated the prediction capability of several constitutive models to characterize the hot deformational flow stress behavior of AA7075 using statistical factors. To predict the flow stress of Al7075, Rasaee et al. [18] proposed a modified Johnson Cook model that takes into account hardening and softening behavior; the accuracy of the modified model is significantly improved by experimental verification. In addition, some scholars have studied the microstructure evolution [19], softening mechanism [20], dislocation mechanics [21], strain rate hardening [22] and other characteristics of 7075 aluminum alloy during hot forming through hot compression experiments, and established a modified constitutive model. In contrast to the research methods of the above scholars, Lee et al. [23] and Yong et al. [24] investigated the heat flow behavior and microstructure evolution of 7075 aluminum alloy under low temperature and pre-cooling conditions, respectively.

A review of the literature on finite element simulation of cutting forces shows that there are few finite element simulation models that predict them separately for conventional and high-speed cutting, and few integrated models that predict them. In this study, the paper primarily focused on determining the impact of various Johnson Cook constants collected from the literature on the modeling of cutting force during conventional and high-speed machining of 7075-T6 aluminum alloy. The three-dimensional finite element model for milling 7075-T6 aluminum alloy was developed using Johnson Cook’s five constitutive equation parameters. The results predicted by the simulation (forces in the X, Y, and Z directions) were compared with the experimental results to verify the validity of the simulation model and to analyze the effect of different pairs of different Johnson Cook constitutive equation parameters on the cutting forces in each direction. The study not only provides an idea and method in the finite element analysis and prediction of cutting forces, but also constructs an integrated model containing the JC constitutive model, the tool geometry and material model, and the workpiece geometry and material model, which can also be applied to the field of digital twin and smart manufacturing in the future.

2. Constitutive Equation Model of 7075-T6 Aluminum Alloy

Metal cutting is a process in which a portion of the workpiece material is plastically deformed by the squeezing action of the tool and then stripped from the surface of the workpiece material and transformed into chips. The constitutive equation of a metallic material is a general equation describing all the basic information about the macroscopic stress variation with strain in a metallic material under certain deformation conditions. To a certain extent, it can describe the relationship between the various thermal parameters of deformation under the action of thermal coupling, such as the interrelation-ship between flow stress and strain, strain rate and temperature. The construction of a material model that can truly reflect the correspondence between stress, strain, strain rate and temperature of the workpiece material is a prerequisite for the correctness and reliability of the dynamic simulation results of the cutting process.

The Johnson Cook model takes into account the three effects of strain hardening, strain rate strengthening and thermal softening that exist in metal materials during cutting and machining, and can reflect the behavior of mechanical changes in metals under large strains, high strain rates, and high temperatures, which can be described by the following model (1) expressions

$$\overline{\sigma }=\left(A+B{\overline{\epsilon }}^n\right)\left[1+C\ln \left(\frac{\dot{\overline{\epsilon }}}{{\dot{\overline{\epsilon }}}_0}\right)\right]\left[1-{\left(\frac{T-T_{room}}{T_{melt}-T_{room}}\right)}^m\right]$$

(1)

where:

$\overline{\sigma }$—the flow stress of the material, MPa;

A—the initial yield stress of the material, MPa;

B—the strain hardening coefficient, MPa;

$\overline{\epsilon }$—the equivalent plastic strain of the material;

n—the hardening coefficient;

C—the strain rate strengthening coefficient;

$\dot{\overline{\epsilon }}$—the equivalent plastic strain rate of the material, s⁻¹;

${\dot{\overline{\epsilon }}}_0$—the reference strain rate of material, s⁻¹;

T—the evolution of temperature; °C

T_room—the transition temperature; °C

T_melt—the melting temperature of the material; °C

m—the thermal softening coefficient.

This model is an empirical constitutive relationship model that can reflect the mechanical behavior of metallic materials at high strains, high strain rates and high temperatures, and is applicable to different metallic materials, and the input interface of the Johnson Cook constitutive model is integrated in Deform-3D. The material constants obtained by several researchers are given in

Table 1. 7075-T6 aluminum alloy material constants obtained by several research papers.

J–C Model	A (MPa)	B(MPa)	n	C	m	Troom (°C)	Tmelt (°C)
JC1 [25]	546	678	0.71	0.024	1.56	25	635
JC2 [26]	665.6	72.6	0.48	0.002	0.79	25	635
JC3 [27]	473	210	0.3813	0.033	0	25	635
JC4 [28]	496	310	0.410	0.000	1.20	25	635
JC5 [29]	317.37	166.95	0.5091	−0.00736	1.5724	25	635

.

3. Finite Element Simulation Analysis of 7075-T6 Aluminum Alloy Machining

Commercial FEM code SFTC Deform TM (V11.0, Scientific Forming Technologies, Inc., Columbus, OH, USA) was used in the simulation machining of aluminum alloy 7075-T6. The software can be used to calculate the cutting force, the temperature between the tool and the workpiece. ALE (Arbitrary Lagrange-Euler) adaptive meshing was used in the simulation to maintain a high-quality mesh and to prevent the analytical calculations from being terminated due to severe mesh distortion, and FE model was developed to validate the formulated constitutive models. The geometry of the three-dimensional FE cutting model is shown in Figure 1. In the meshed model, the workpiece material is represented as an elastic-viscoplastic deformable body with 50,000 iso-parametric quadrilateral elements, while the tool is modeled as rigid, represented with 50,000 elements. The boundary conditions are to constrain the translational degrees of freedom in the X, Y, and Z directions of each face of the workpiece except the top.

The experimental conditions of tool geometry and dimensions used in the numerical simulations were consistent, the simulated cutting conditions were identical to those on the actual machine, and the mechanical and thermal boundary conditions of the materials used (

Table 2. Mechanical and thermo-physical properties of materials considered in finite element simulations.

Material/ Parameter	Young’s Modulus (GPa)	Thermal Conductivity (W/m·°C)	Specific Heat Capacity (J/kg·°C)	Poisson’s Ratio	Density (kg/m3)
Al 7075-T6	68.9	180.175	910	0.3	2700
WC	650	58.988	400	0.25	11,900

) were defined accordingly [30,31] to allow heat transfer between the workpiece and the tool. No cutting fluid was used in the tests. According to the test conditions and the considered machining environment, the capability of the developed intrinsic model in terms of relevant thermo-force was demonstrated.

4. Experimental Work

The studied material is the high-strength aluminum alloy 7075-T6, which is well accepted in the manufacturing of several aeronautical structural parts. Dry machining tests were conducted on a high precision five-axis JDGR200_A10SH NC machine-tool (Beijing Jingdiao Technology Group Co., Ltd., Beijing, China) and using a taper ball end milling cutter with 2 flutes; the cutter material was uncoated carbide. The cutting forces were measured with the 9257B Kistler dynamometer and high-speed data acquisition devices HP3852S (Kistler, Winterthur, Switzerland). With the experimental set-up indicated in Figure 2 and Figure 3, dry cutting was used throughout the experiment. A set of machining tests were carried out as per the experimental conditions adopted in

Table 3. Conditions adopted in FE simulation and machining experiment.

Parameter	Conditions
Workpiece material	7075-T6 aluminum alloy
Chemical composition (wt.%)	Zn-5.6, Mg-2.5, Cu-1.6, Fe-0.5, Si-0.4, Mn-0.3, Cr-0.23, Ti-0.2, Al-Rem.
Cutting condition	Spindle speed n = 5000, 16,000 r/min, Cutting depth ap = 0.2 mm, Cutting width aw = 0.6 mm.
Machining test environments	Dry machining tests
Cutting tool and tool geometry	Rake angle (γ) = 8°, Clearance angle (α) = 10°, Helical angle (β) = 30°, Taper angle of the ball end mill (η) = 6°, Radius of the ball end mill (R) = 0.5 mm, Length of cutting edge in axis direction (L) = 15 mm.

and the workpiece is made from a 7075-T6 aluminum alloy bar, measuring Φ150 mm × 60 mm, solid solution treated and pre-stretched. To reduce the effect of clamping forces on the deformation of the part, the upper part of the workpiece was machined into a square of 100 mm × 100 mm × 35 mm and then divided into 25 pieces of 12 mm × 12 mm × 2 mm. Two bolts held the lower part of the workpiece to the dynamometer and two pressure plates held the dynamometer to the machine table.

The equipment and workpiece materials required for the experiment were shown in

Table 4. Experimental equipment information.

Equipment	Experimental Condition
Machine tool	JDGR200 A10SH five-axis high precision machining center
Cutting tool	φ1 mm carbide double-edge taper ball milling cutter without coating
Workpiece material	7075-T6 Aluminum alloy
Milling force measuring equipment	9257B Kistler dynamometer
Data acquisition card	HP3852S
Charge amplifier	5070A

.

5. Results and Discussion

5.1. FEA Simulation in Conventional Machining

The predicted and experimentally measured cutting force of each dimension were compared and discrepancies highlighted to verify the FEM cutting model.

For each of the five Johnson−Cook constitutive models, the average experimental and predicted cutting forces in the X, Y, and Z directions are shown in Figure 4. As seen in Figure 4, the cutting forces for each direction with five different material coefficients, the predictions of the cutting force for the material coefficients of the JC1 model are large and vary significantly compared to the experimental results. When considering the material coefficients of the JC2 and JC5 models, the difference between the simulation-derived cutting forces and the experimental results is close, but small compared to the experimental values. The material coefficients of the JC3 model ignore the effect of thermal softening of the material on the flow stress and cannot be simulated using the Johnson−Cook constitutive model. The predicted results of the material coefficients of the JC4 model for cutting force are less different from the experimental results than the other models, and they are in good agreement with the experimental results.

The experimental cutting forces, predicted cutting forces, and errors in the X, Y, and Z directions for the five Johnson−Cook constitutive models under conventional cutting conditions are reported in

Table 5. Comparison between experimentally and numerically obtained average cutting force (n = 5000 r/min; a_p = 0.2 mm, a_w = 0.6 mm. Values in brackets are error values).

	Cutting Force (N)
	Fx	Fy	Fz
Experimental results	32.75	9.45	18.46
JC1	54.38 (66.05%)	32.75 (246.56%)	41.35 (124.00%)
JC2	13.32 (−59.33%)	7.62 (−19.37%)	11.28 (−38.89%)
JC3	-	-	-
JC4	24.35 (−25.65%)	7.85 (−16.93%)	18.41 (−0.2409%)
JC5	17.58 (−46.32%)	5.04 (−46.67%)	14.10 (−23.62%)

.

The predicted cutting forces in the X-direction are 1.66 times greater than the experimental cutting forces, the predicted cutting forces in the Y-direction are 3.47 times greater than the experimental cutting forces and the predicted cutting forces in the Z-direction are 2.24 times greater than the experimental cutting forces, as can be seen from Table 3. This is because the coefficients (A, B, n, C and m) of the Al7075-T6 material model were derived at room temperature and 250 °C high temperature and do not truly reflect the changes in high strain rate tensile stress-strain data during the cutting process, so the errors in the predicted cutting forces derived would be significant. The material coefficients from the JC2 model give a small simulated cutting force and are much smaller than the experimental cutting force figures, which are 2.46 times greater in the X direction, 1.24 times greater in the Y direction and 1.64 times greater in the Z direction. This is because the coefficients (A, B, n, C and m) used for the Al7075-T6 material model were derived at a reference temperature of 300 K and a strain rate of 1 s⁻¹, which does not cover the actual temperature and strain rate range for the entire cutting process, so the error in the predicted cutting forces derived is significant. The material coefficients of the JC3 model cannot be simulated to derive cutting forces because the JC3 model ignores the effect of thermal softening of the material on flow stresses and cannot be simulated using the Johnson−Cook constitutive model. The predicted cutting forces derived from the material coefficients of the JC4 model are closest to the experimental cutting forces, and this material coefficient is obtained from the CTH and EPIC band codes. The analysis was obtained from the results of strain testing of bullet impact 7075-T6 thin plates. CTH is a Eulerian code for modelling material properties at large deformations and high strain rates. EPIC is a Lagrangian code that also has the ability to model the behavior of materials at high strain rates. The predicted cutting forces from the material coefficients of the JC5 model are also small compared to the test cutting forces, which are 1.86 times greater in the x-direction, 1.88 times greater in the y-direction and 1.31 times greater in the z-direction. This is because the coefficients (A, B, n, C and m) used for the Al7075-T6 material model were derived at reference temperatures of 300–623 K and strain rates of 0.1, 0.01, 0.001, 0.0001 s⁻¹. This covers part of the actual temperature and strain rate range of the cutting process, but the elastic state is neglected in the true stress-true strain curve when the standard equation is used to convert the load-displacement data into true stress-strain data. Therefore, the resulting predicted cutting forces are also subject to error.

The influence law of each parameter of the Johnson−Cook constitutive structure model on the cutting force is shown in Figure 5. From Figure 5, it can be seen that: parameter A is the initial yield stress of the material, and its influence on the cutting force increases at first then decreases, reaching the maximum value at JC1, and then the cutting force starts to decrease with the increase of A value, and the influence on the cutting force is more significant at the stage of change from JC4 to JC1. The parameter B is the strain hardening parameter of the material, and the change in cutting force is positively related to the change of parameter B. As the parameter B increases, the cutting force also increases. The parameter n is the hardening index of the material, and its influence on the cutting force decreases first and then increases, and the influence on the cutting force is more significant at the stage of change from JC5 to JC1. The parameter C is the strain rate strengthening parameter of the material, and its influence on the cutting force increases first, then decreases and finally increases, and the influence on the cutting force is more significant at the stage of change from JC2 to JC1. The parameter m is the thermal softening parameter of the material, and its influence on the cutting force increases first and then decreases, and the influence on the cutting force is more significant at the stage of change from JC1 to JC5.

5.2. FEA Simulation in High−Speed Machining

High-speed machining is widely used in many industries as an advanced manufacturing technology with rapid development in recent years. The formation of cutting force in high-speed machining is a complex process of material deformation and removal. In the research field of high-speed machining, the finite element analysis and prediction of cutting force is a difficult topic that draws significant interest. To accurately calculate the cutting force through finite element simulation, the parameters in the constitutive equation model need to be more accurate.

Figure 6 shows the predicted cutting forces for the Johnson−Cook constitutive model for five different sets of material factors. The results show that the cutting forces for high-speed machining are lower than those for conventional machining, and the predicted cutting forces for the material factor of the JC1 model are the highest. With the material factor of the JC2 model, the difference between the simulated cutting forces and the experimental results is close, but small compared to the experimental values. When using the material factor of the JC4 model, the resulting cutting forces are close to the experimental values but are not as large as the experimental values. The difference between the predicted cutting forces and the experimental values for the material coefficients of the JC5 model is smaller than the other models and agrees well with the experimental results. A possible reason for this could be that the constants for the Johnson−Cook model in JC5 work were determined by mechanical testing of high strain rates over a reasonable range of values (i.e., true strain, strain rate and temperature), which is more consistent with the high strain rates of high−speed cutting, so the resulting predicted cutting forces are closer to the experimental results.

The experimental cutting forces, predicted cutting forces, and errors in the X, Y, and Z directions for the five Johnson−Cook constitutive models under high-speed cutting conditions are reported in

Table 6. Comparison between experimentally and numerically obtained average cutting force (n = 16,000 r/min; ap = 0.2 mm, aw = 0.6 mm. Values in brackets are error values).

	Cutting Force (N)
	Fx	Fy	Fz
Experimental results	13.79	8.32	12.63
JC1	40.00 (190.07%)	23.44 (181.73%)	34.58 (173.79%)
JC2	16.10 (16.75%)	6.35 (−23.68)	10.68 (−15.44%)
JC3	-	-	-
JC4	20.79 (50.76%)	9.08 (9.13%)	16.52 (30.80%)
JC5	14.58 (5.73%)	8.06 (3.13%)	11.28 (10.69%)

.

Table 6 shows some of the data for the high-speed cutting conditions. The analysis process is consistent with the conventional cutting conditions. The data show that the error in predicting cutting forces is smaller for the high-speed cutting condition than for the conventional cutting condition. The JC5 model parameters predict the cutting forces well for the high-speed cutting condition. This is because the model parameters were determined by mechanical testing at high strain rates within a reasonable range of values (i.e., true strain, strain rate and temperature), which is more consistent with the high strain rates of high-speed cutting, so the resulting predicted cutting forces are closer to the experimental results.

As can be seen in Figure 7, the pattern of influence of parameters A, B, n, C and m on cutting forces is basically the same as for conventional cutting. However, when the JC1, JC2, JC4 and JC5 models are used, the trend of the predicted cutting force values decreases as the spindle speed increases, which is consistent with the trend of the experimental values of cutting force. This can also prove that the cutting force values are smaller for high-speed cutting conditions than for conventional cutting.

6. Conclusions

The aim of this research work was to investigate the influence of material flow stress parameters on the finite element analysis of the machining process of 7075 aluminum alloy under different cutting conditions. The Johnson−Cook constitutive structure equations with five different sets of material constants were implemented in a numerical machining model, and the experimental results were compared with the predicted values. The applicability of the finite element modelling of the machining process is verified by analyzing the predicted results of the cutting forces. The finite element simulation results show that the cutting forces during the cutting process are better predicted using certain models and are in good agreement with the experimental measurements. The average relative error in the prediction of cutting forces for both conventional and high-speed machining using the JC1 model is large, with the largest error of 246.56% for Fy under conventional cutting conditions. The predicted cutting forces from the JC2 model also have large errors, but are much smaller compared to JC1, with the largest error of −59.33% for Fx under conventional cutting conditions. The JC3 model ignores the effect of thermal softening of the material on the cutting forces and the numerical model is incomplete from the point of view of the cutting process and does not allow for finite element simulation of the cutting process. In predicting the cutting forces under conventional conditions, the material coefficients of the JC4 model differed little from the experimental results and were in good agreement with the experimental results, with the smallest error value of −0.2409% for Fz. The material coefficients of the JC5 model showed the smallest difference with the predicted cutting forces at high speeds and were smaller than the other models, so that a reasonable prediction of cutting forces could be made, with a minimum error value of −3.13% for Fy. The effect of parameter changes in the Johnson−Cook intrinsic model on the cutting force simulation results was investigated, and it was found that the temperature softening factor m and the strain strengthening factor B had the most significant effect on the cutting force.

The influence of the variation of the parameters of the Johnson−Cook constitutive model on the simulation results of cutting forces is investigated to provide reference suggestions for the study of the intrinsic model. The finite element analysis method proposed in this paper can be used to study the machining process of 7075 aluminum alloy, and can predict the actual cutting force better. Moreover, the constructed finite element analysis model is an integrated model that combines the JC intrinsic model, geometric and material models of the tool, and geometric and material models of the workpiece, which can be applied not only to the prediction of cutting forces for different cutting speed working conditions, but also in the field of digital twin and intelligent manufacturing.