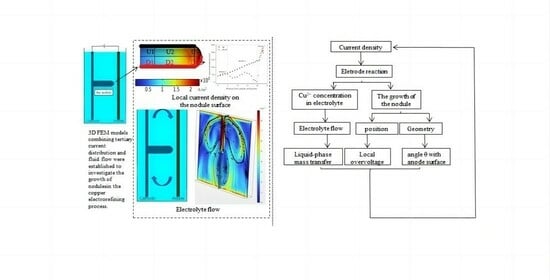
Numerical Simulation of Cathode Nodule Local Effects
Abstract
:1. Introduction
2. Model Description
2.1. Geometry Model
2.2. Numerical Model
2.3. Model Boundary Conditions
3. Results and Discussion
3.1. Characteristics and Analysis of the Electrolytic Process
3.2. Current Density Distribution of Nodule Surface and Analysis
3.3. Surface Concentration Effects of Nodule
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Mori, K.; Yamakawa, Y.; Oue, S.; Taninouchi, Y.-K.; Nakano, H. Effect of Impurity Ions and Additives in Solution of Copper Electrorefining on the Passivation Behavior of Low-Grade Copper Anode. Mater. Trans. 2023, 64, 242–251. [Google Scholar] [CrossRef]
- Schlesinger, E.; King, J.; Sole, C.; Davenport, G. Extractive Metallurgy of Copper, 5th ed.; Electrolytic Refining; Pergamon Press: Oxford, UK, 2011; pp. 251–280. [Google Scholar] [CrossRef]
- Andersen, T.N.; Pitt, C.H.; Livingston, L.S. Nodulation of Electrodeposited Copper Due to Suspended Particulate. J. Appl. Electrochem. 1983, 13, 429–438. [Google Scholar] [CrossRef]
- Dutrizac, J.E.; Chen, T.T. A Mineralogical Study of Nodulated Copper Cathodes. J. Proc. Copper Int. Conf. 1999, 383–403. [Google Scholar]
- Wang, Z.; Meng, Y.; Li, C.; Tie, J.; Zhao, R. Effect of nodules on electrolyte flow and Cu2+ concentration distribution in copper electrolytic refining. In Advances in Energy, Environment and Chemical Engineering; Abdullah, A.Z., Osman, A.F., Eds.; CRC Press: Boca Raton, FL, USA, 2023; pp. 309–313. [Google Scholar]
- Meng, Y.; Liu, H.; Li, C. Cathodic current change and nodulation morphology during short circuit of copper electrolysis. Chin. J. Nonferrous Met. 2022, 32, 262–270. [Google Scholar] [CrossRef]
- Zhao, J.; Meng, Y.; Li, C.; Tie, J. The effect of nodulation on the distribution of concentration and current density during copper electrolytic refining. J. Phys. Conf. Ser. 2022, 2285, 012015. [Google Scholar] [CrossRef]
- Adachi, K.; Nakai, Y.; Kitada, A.; Fukami, K.; Murase, K. FEM Simulation of Nodulation in Copper Electro-Refining. In Rare Metal Technology; Springer: Cham, Switzerland, 2018. [Google Scholar] [CrossRef]
- Nakai, Y.; Adachi, K.; Kitada, A.; Fukami, K.; Murase, K. Experimental Modeling of Nodulation in Copper Electrorefining. In Rare Metal Technology; Springer: Cham, Switzerland, 2018. [Google Scholar] [CrossRef]
- Zeng, Q.; Li, C.; Meng, Y.; Tie, J.; Zhao, R.; Zhang, Z. Analysis of interelectrode short-circuit current in industrial copper electrorefining cells. Measurement 2020, 164, 108015. [Google Scholar] [CrossRef]
- Bard, A.J.; Faulkner, L.R. Electrochemical Methods: Fundamentals and Applications; Chemical Industry Press: Beijing, China, 2005. [Google Scholar]
- Zeng, W. Experimental and Validated Modeling Studies of Electrolyte Flow and Anode Slime Behavior and Transport in Copper Electrorefining; University of Utah: Salt Lake City, UT, USA, 2016. [Google Scholar]
- Miyamoto, M.; Mitsuno, S.; Kitada, A.; Fukami, K.; Murase, K. Mechanism of nodular growth in copper electrorefining with the inclusion of impurity particles under natural convection. Hydrometallurgy 2023, 216, 106013. [Google Scholar] [CrossRef]
- Zeng, W.; Free, M.L.; Werner, J.; Wang, S. Simulation and Validation Studies of Impurity Particle Behavior in Copper Electrorefining. J. Electrochem. Soc. 2015, 162, E338–E352. [Google Scholar] [CrossRef]
- Zeng, W.; Werner, J.; Free, M.L. Experimental studies on impurity particle behavior in electrolyte and the associated distribution on the cathode in the process of copper electrorefining. Hydrometallurgy 2015, 156, 232–238. [Google Scholar] [CrossRef]
- Zeng, W.; Free, M.L.; Wang, S. Simulation Study of Electrolyte Flow and Slime Particle Transport in a Newly Designed Copper Electrorefining Cell. ECS Trans. 2016, 72, 23–42. [Google Scholar] [CrossRef]
- Zeng, W.; Wang, S.; Free, M.L. Experimental and Simulation Studies of Electrolyte Flow and Slime Particle Transport in a Pilot Scale Copper Electrorefining Cell. J. Electrochem. Soc. 2016, 163, E111–E122. [Google Scholar] [CrossRef]
- Kim, K.R.; Choi, S.Y.; Paek, S.; Park, J.Y.; Hwang, I.S.; Jung, Y. Electrochemical Hydrodynamics Modeling Approach for a Copper Electrowinning Cell. Int. J. Electrochem. Sci. 2013, 8, 12333–12347. [Google Scholar] [CrossRef]
- Brown, D.A.; MacDonald, A.R.; McCarron, E.A.; Zarwell, S.; Bernhard, T.; Brüning, R. Properties of an electroless copper process as a function of nickel and cyanide ion concentrations. J. Appl. Electrochem. 2021, 51, 795–802. [Google Scholar] [CrossRef]
- Graydon, J.W.; Kirk, D.W. Suspension codeposition in electrowinning cells: The role of hydrodynamics. Can. J. Chem. Eng. 1991, 69, 564–570. [Google Scholar] [CrossRef]
- Najminoori, M.; Mohebbi, A.; Arabi, B.G.; Daneshpajouh, S. CFD simulation of an industrial copper electrowinning cell. Hydrometallurgy 2015, 153, 88–97. [Google Scholar] [CrossRef]
- Leahy, M.J.; Schwarz, M.P. Experimental Validation of a Computational Fluid Dynamics Model of Copper Electrowinning. Met. Mater. Trans. B 2010, 41, 1247–1260. [Google Scholar] [CrossRef]
- Rosa-Ortiz, S.M.; Khorramshahi, F.; Takshi, A. Study the impact of CuSO4 and H2SO4 concentrations on lateral growth of hydrogen evolution assisted copper electroplating. J. Appl. Electrochem. 2019, 49, 1203–1210. [Google Scholar] [CrossRef]
- Le, A.S. Improved Production Practice of Copper Electrolysis by Enhancing Electrolyte Temperature. J. China Nonferrous Metall. 2017, 46, 11–15. [Google Scholar]
- Li, M.Z.; Huang, J.T.; Tong, C.R. Numerical Analysis of Electrothermal Field in Copper Electrolyzer. Nonferrous Met. Sci. Eng. 2016, 7, 50–55. [Google Scholar]
- Kalliomäki, T.; Aji, A.T.; Jafari, S.; Leskinen, W.; Wilson, B.P.; Aromaa, J.; Lundström, M. Industrial validation of conductivity and viscosity models for copper electrolysis processes. Miner. Eng. 2021, 171, 107069. [Google Scholar] [CrossRef]
- Khayatzadeh, H.; Tahmasebi, K. Optimizing Electrolyte Conditions for the Elimination of Nodules in Copper Electrorefining Process. JOM 2024, 76, 452–463. [Google Scholar] [CrossRef]
- Wang, H.; Wang, Q.; Xia, W.; Ren, B. Effect of Jet Flow between Electrodes on the Cathode Quality in Copper Electrorefining with High Current Density. Metals 2018, 8, 833. [Google Scholar] [CrossRef]
- Sahlman, M.; Aromaa, J.; Lundström, M. Detachment and flow behaviour of anode slimes in high nickel copper electrorefining. Physicochem. Probl. Miner. Process. 2024, 60, 186194. [Google Scholar] [CrossRef]
- Correa, P.P.; Cipriano, A.; Nunez, F.; Salas, J.C.; Lobel, H. Forecasting Copper Electrorefining Cathode Rejection by Means of Recurrent Neural Networks with Attention Mechanism. IEEE Access 2021, 9, 79080–79088. [Google Scholar] [CrossRef]
- Pryor, R.W. Multiphysics Modeling Using COMSOL: A First Principles Approach; Jones and Bartlett Publishers, LLC: Sudbury, MA, USA, 2011. [Google Scholar]
- Adachi, K.; Nakai, Y.; Mitsuno, S.; Miyamoto, M.; Kitada, A.; Fukami, K.; Murase, K. The Mechanism of Nodular Growth in Copper Electrorefining. J. MMIJ 2020, 136, 8–13. [Google Scholar] [CrossRef]
- Price, D.C.; Davenport, W.G. Physico-chemical properties of copper electrorefining and electrowinning electrolytes. Met. Trans. B 1981, 12, 639–643. [Google Scholar] [CrossRef]
- Zeng, W.; Wang, S.; Free, M.L. Two-Phase Flow Modeling of Copper Electrorefining Involving Impurity Particles. J. Electrochem. Soc. 2017, 164, E233–E241. [Google Scholar] [CrossRef]
- Miyamoto, M.; Ishikawa, Y.; Fukami, K.; Murase, K. Surface Roughening and Growth-Promoting Effects of Nickel and Antimony on Nodules in Copper Electrorefining. Met. Mater. Trans. B 2023, 54, 3579–3590. [Google Scholar] [CrossRef]
- Meng, Y.; Liu, H.; Li, C. Study on the growth behavior of nodules under the electrolytic conditions of copper industry. Hydrometall. China 2021, 40, 446–450. [Google Scholar]









| Description | Value |
|---|---|
| Temperature | 338.15 K |
| Exchange current density | 150 A/m2 |
| Anode voltage | 0.25 V |
| Cathode voltage | 0 V |
| Cu2+ diffusion coefficient | 1.13 × 10−9 m2/s |
| H+ diffusion coefficient | 2.26 × 10−9 m2/s |
| SO42− diffusion coefficient | 3.77 × 10−10 m2/s |
| Anodic transfer coefficient | 1.3 |
| Cathodic transfer coefficient | 0.7 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, X.; Li, C.; Tie, J. Numerical Simulation of Cathode Nodule Local Effects. Metals 2024, 14, 457. https://doi.org/10.3390/met14040457
Wang X, Li C, Tie J. Numerical Simulation of Cathode Nodule Local Effects. Metals. 2024; 14(4):457. https://doi.org/10.3390/met14040457
Chicago/Turabian StyleWang, Xiaoyu, Chun Li, and Jun Tie. 2024. "Numerical Simulation of Cathode Nodule Local Effects" Metals 14, no. 4: 457. https://doi.org/10.3390/met14040457
APA StyleWang, X., Li, C., & Tie, J. (2024). Numerical Simulation of Cathode Nodule Local Effects. Metals, 14(4), 457. https://doi.org/10.3390/met14040457