Molecular Dynamics Simulation of Crack Propagation in Nanoscale Polycrystal Nickel Based on Different Strain Rates
Abstract
:1. Introduction
2. Modeling and Methods
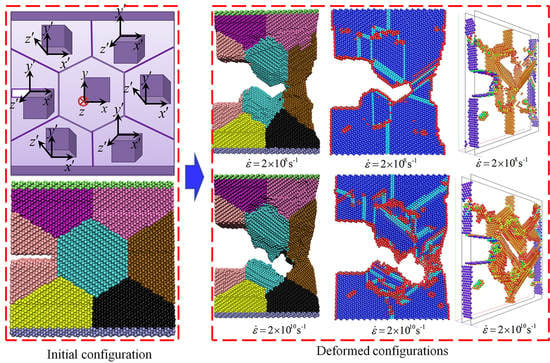
2.1. Simulation Model
2.2. Potential Function
2.3. Simulation Methods
3. Results and Discussion
4. Conclusions
- (1)
- The strain rate has an important effect on mechanisms of crack propagation in nanoscale polycrystal nickel. The yield stress is sensitive to the strain rate, and the yield stress of nanoscale polycrystal nickel at the strain rate of 2 × 1010 s−1 is much higher than the counterpart at the strain rate of 2 × 108 s−1.
- (2)
- When the nanoscale polycrystal nickel is subjected to plastic deformation in the case of 2 × 1010 s−1, local non-3D-crystalline atoms are induced and Lomer-Cottrell locks are formed. However, in the case of 2 × 108 s−1, neither non-3D-crystalline atoms nor Lomer-Cottrell locks are induced, but stacking faults are captured.
- (3)
- Lomer-Cottrell locks are able to impede the movement of dislocations and thus lead to the pile-up of dislocations. In addition, the non-3D-crystalline atoms are easy to be induced near the Lomer-Cottrell locks. Consequently, Lomer-Cottrell locks contribute to accelerating the propagation of crack.
- (4)
- The orientation difference between the adjacent grains leads to slipping of dislocations along the different directions, which results in the initiation of a void in the vicinity of the triple junction of grain boundaries. The coalescence of the void with the crack contributes to accelerating the propagation of cracks.
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Yamakov, V.I.; Warner, D.H.; Zamora, R.J.; Saether, E.; Curtin, W.A.; Glaessgen, E.H. Investigation of crack tip dislocation emission in aluminum using multiscale molecular dynamics simulation and continuum modeling. J. Mech. Phys. Solids 2014, 65, 35–53. [Google Scholar] [CrossRef]
- Cui, Y.; Liu, Z.; Zhuang, Z. Quantitative investigations on dislocation based discrete-continuous model of crystal plasticity at submicron scale. Int. J. Plasticity 2015, 65, 54–72. [Google Scholar] [CrossRef]
- Shilkrot, L.; Miller, R.; Curtin, W.A. Multiscale plasticity modeling: Coupled atomistics and discrete dislocation mechanics. J. Mech. Phys. Solids 2004, 52, 755–787. [Google Scholar] [CrossRef]
- Han, Q.; Wang, Y.; Yin, Y.; Wang, D. Determination of stress intensity factor for mode I fatigue crack based on finite element analysis. Eng. Fract. Mech. 2015, 138, 118–126. [Google Scholar] [CrossRef]
- Benz, C.; Sander, M. Reconsiderations of fatigue crack growth at negative stress ratios: Finite element analyses. Eng. Fract. Mech. 2015, 145, 98–114. [Google Scholar] [CrossRef]
- Ghosh, S.; Anahid, M. Homogenized constitutive and fatigue nucleation models from crystal plasticity FE simulations of Ti alloys, Part 1: Macroscopic anisotropic yield function. Int. J. Plasticity 2013, 47, 182–201. [Google Scholar] [CrossRef]
- Ghosh, S.; Anahid, M. Homogenized constitutive and fatigue nucleation models from crystal plasticity FE simulations of Ti alloys, Part 2: Macroscopic probabilistic crack nucleation model. Int. J. Plasticity 2013, 48, 111–124. [Google Scholar]
- Proudhon, H.; Li, J.; Wang, F.; Roos, A.; Chiaruttini, V.; Forest, S. 3D simulation of short fatigue crack propagation by finite element crystal plasticity and remeshing. Int. J. Fatigue 2016, 82, 238–246. [Google Scholar] [CrossRef]
- Li, J.; Proudhon, H.; Roos, A.; Chiaruttini, V.; Forest, S. Crystal plasticity finite element simulation of crack growth in single crystals. Comp. Mater. Sci. 2014, 94, 191–197. [Google Scholar] [CrossRef]
- Kartal, M.E.; Cuddihy, M.A.; Dunne, F.P.E. Effects of crystallographic orientation and grain morphology on crack tip stress state and plasticity. Int. J. Fatigue 2014, 61, 46–58. [Google Scholar] [CrossRef]
- Sabnis, P.A.; Mazière, M.; Forest, S.; Arakere, N.K.; Ebrahimi, F. Effect of secondary orientation on notch-tip plasticity in superalloy single crystals. Int. J. Plasticity 2012, 28, 102–123. [Google Scholar] [CrossRef]
- Li, L.; Shen, L.; Proust, G. Fatigue crack initiation life prediction for aluminium alloy 7075 using crystal plasticity finite element simulations. Mech. Mater. 2015, 81, 84–93. [Google Scholar] [CrossRef]
- Lin, B.; Zhao, L.G.; Tong, J. A crystal plasticity study of cyclic constitutive behaviour, crack-tip deformation and crack-growth path for a polycrystalline nickel-based superalloy. Eng. Fract. Mech. 2011, 78, 2174–2192. [Google Scholar] [CrossRef] [Green Version]
- Huang, M.; Zhao, L.; Tong, J.; Li, Z. Discrete dislocation dynamics modelling of mechanical deformation of nickel-based single crystal superalloys. Int. J. Plasticity 2012, 28, 141–158. [Google Scholar] [CrossRef] [Green Version]
- Quek, S.S.; Wu, Z.; Zhang, Y.W.; Srolovitz, D.J. Polycrystal deformation in a discrete dislocation dynamics framework. Acta. Mater. 2014, 75, 92–105. [Google Scholar] [CrossRef]
- Fan, H.; Aubry, S.; Arsenlis, A.; El-Awady, J.A. The role of twinning deformation on the hardening response of polycrystalline magnesium from discrete dislocation dynamics simulation. Acta Mater. 2015, 92, 126–139. [Google Scholar] [CrossRef]
- Segurado, J.; Llorca, J. Dsicrete dislocation dynamics analysis of the effect of lattice orientation on void growth in single crystals. Int. J. Plasticity 2010, 26, 806–819. [Google Scholar] [CrossRef] [Green Version]
- Liang, S.; Huang, M.; Li, Z. Discrete dislocation modeling on interaction between type-I blunt crack and cylindrical void in single crystals. Int. J. Solids Struct. 2015, 56–57, 209–219. [Google Scholar] [CrossRef]
- Huang, M.; Tong, J.; Li, Z. A study of fatigue crack tip characteristics using discrete dislocation dynamics. Int. J. Plasticity 2014, 54, 229–246. [Google Scholar] [CrossRef]
- Sung, P.H.; Chen, T.C. Studies of crack growth and propagation of single-crystal nickel by molecular dynamics. Comp. Mater. Sci. 2015, 102, 151–158. [Google Scholar] [CrossRef]
- Zhang, J.; Ghosh, S. Molecular dynamics based study and characterization of deformation mechanisms near a crack in a crystalline material. J. Mech. Phys. Solids 2013, 61, 1670–1690. [Google Scholar] [CrossRef]
- Zhou, Y.; Yang, Z.; Lu, Z. Dynamic crack propagation in copper bicrystals grain boundary by atomistic simulation. Mater. Sci. Eng. A 2014, 599, 116–124. [Google Scholar] [CrossRef]
- Shimokawaa, T.; Tsuboi, M. Atomic-scale intergranular crack-tip plasticity in tilt grain boundaries acting as an effective dislocation source. Acta Mater. 2015, 87, 233–247. [Google Scholar] [CrossRef]
- Zhang, Y.; Jiang, S.; Zhu, X.; Zhao, Y. A molecular dynamics study of intercrystalline crack propagation in nano-nickel bicrystal films with (0 1 0) twist boundary. Eng. Fract. Mech. 2016, 168, 147–159. [Google Scholar] [CrossRef]
- Foiles, S.M.; Baskes, M.I.; Daw, M.S. Embedded-atom-method functions for the FCC metals Cu, Ag, Au, Ni, Pd, Pt, and their alloys. Phys. Rev. B 1986, 33, 7983–7991. [Google Scholar] [CrossRef]
- Plimpton, S.; Parallel, F. Fast parallel algorithms for short-range molecular dynamics. J. Comput. Phys. 1995, 117, 1–19. [Google Scholar] [CrossRef]
- Kelchner, C.L.; Plimpton, S.J.; Hamilton, J.C. Dislocation nucleation and defect structure during surface indentation. Phys. Rev. B 1998. [Google Scholar] [CrossRef]
- Tsuzuki, H.; Branicio, P.S.; Rino, J.P. Structural characterization of deformed crystals by analysis of common atomic neighborhood. Comput. Phys. Commun. 2007, 177, 518–523. [Google Scholar] [CrossRef]
- Li, J. AtomEye: An efficient atomistic configuration viewer. Model. Simul. Mater. Sci. Eng. 2003, 11, 173–177. [Google Scholar] [CrossRef]
- Humphrey, W.; Dalke, A.; Schulten, K. VMD-Visual Molecular Dynamics. J. Mol. Graph. 1996, 14, 33–38. [Google Scholar] [CrossRef]










© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Y.; Jiang, S. Molecular Dynamics Simulation of Crack Propagation in Nanoscale Polycrystal Nickel Based on Different Strain Rates. Metals 2017, 7, 432. https://doi.org/10.3390/met7100432
Zhang Y, Jiang S. Molecular Dynamics Simulation of Crack Propagation in Nanoscale Polycrystal Nickel Based on Different Strain Rates. Metals. 2017; 7(10):432. https://doi.org/10.3390/met7100432
Chicago/Turabian StyleZhang, Yanqiu, and Shuyong Jiang. 2017. "Molecular Dynamics Simulation of Crack Propagation in Nanoscale Polycrystal Nickel Based on Different Strain Rates" Metals 7, no. 10: 432. https://doi.org/10.3390/met7100432
APA StyleZhang, Y., & Jiang, S. (2017). Molecular Dynamics Simulation of Crack Propagation in Nanoscale Polycrystal Nickel Based on Different Strain Rates. Metals, 7(10), 432. https://doi.org/10.3390/met7100432