The Influence of Thermal History on the Multistage Transformation of NiTi Shape-Memory Alloys
Abstract
:1. Introduction
2. Experimental Results
2.1. Transformation Evolution under Cycling
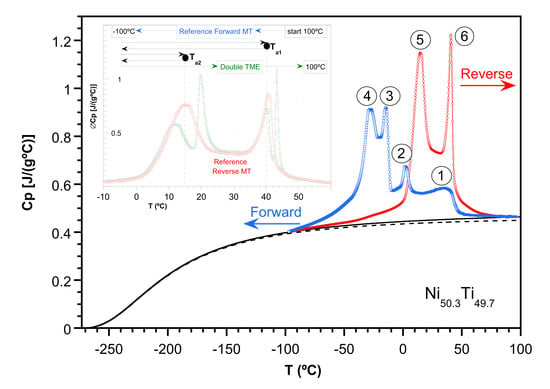
2.2. Study of the Transformation Stages
- -
- Cooling down to those temperatures that include stage 1 (Ts1 = 24 °C and Ts2 = 10 °C) increases successively the Cp of stage 6 upon heating.
- -
- Cooling down to Ts below stage 2 (Ts3 = −10 °C) shows an equal increase for Cp at both stages 5 and 6 upon heating.
- -
- Cooling down to Ts below stage 3 (Ts4 = −20 °C) mainly increases the Cp values around stage 6 up to its total final value upon heating.
- -
- Finally, cooling down to Ts below stage 4 (Ts5 = −40, Ts6 = −60 °C) only increases the Cp of stage 5, approaching its total final value upon heating.
2.3. Evidence of the Temperature Memory Effect
3. Summary and Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Otsuka, K.; Wayman, C.M. Shape Memory Materials; Cambridge University Press: Cambridge, UK, 1999; ISBN 978-0-521-66384-7. [Google Scholar]
- Lagoudas, D.C. Shape Memory Alloys: Modeling and Engineering Applications; Springer: Berlin, Germany, 2008; ISBN 978-0-387-47685-8. [Google Scholar]
- Ohkata, I.; Tsuchiya, K.; Miyazaki, S. Shape Memory and Superelastic Alloys: Applications and Technologies; Yamauchi, K., Ed.; Reprint Edition; Woodhead Publishing: Cambridge, UK, 2016; ISBN 978-0-08-101701-2. [Google Scholar]
- Schryvers, D.; Potapov, P.; Santamarta, R.; Tirry, W. Applications of advanced transmission electron microscopic techniques to Ni–Ti based shape memory materials. Mater. Sci. Eng. A 2004, 378, 11–15. [Google Scholar] [CrossRef]
- Otsuka, K.; Ren, X. Physical metallurgy of Ti–Ni-based shape memory alloys. Prog. Mater. Sci. 2005, 50, 511–678. [Google Scholar] [CrossRef]
- Povoden-Karadeniz, E.; Cirstea, D.C.; Lang, P.; Wojcik, T.; Kozeschnik, E. Thermodynamics of Ti–Ni shape memory alloys. Calphad 2013, 41, 128–139. [Google Scholar] [CrossRef]
- Frenzel, J.; George, E.P.; Dlouhy, A.; Somsen, C.; Wagner, M.F.-X.; Eggeler, G. Influence of Ni on martensitic phase transformations in NiTi shape memory alloys. Acta Mater. 2010, 58, 3444–3458. [Google Scholar] [CrossRef]
- Matsumoto, H. Transformation behaviour with thermal cycling in NiTi alloys. J. Alloys Compd. 2003, 350, 213–217. [Google Scholar] [CrossRef]
- Pattabi, M.; Ramakrishna, K.; Mahesh, K.K. Effect of thermal cycling on the shape memory transformation behavior of NiTi alloy: Powder X-ray diffraction study. Mater. Sci. Eng. A 2007, 448, 33–38. [Google Scholar] [CrossRef]
- Sitepu, H.; Schmahl, W.; Allafi, J.; Eggeler, G.; Dlouhy, A.; Toebbens, D.; Tovar, M. Neutron diffraction phase analysis during thermal cycling of a Ni-rich NiTi shape memory alloy using the Rietveld method. Scr. Mater. 2002, 46, 543–548. [Google Scholar] [CrossRef]
- Urbina, C.; De la Flor, S.; Ferrando, F. Effect of thermal cycling on the thermomechanical behaviour of NiTi shape memory alloys. Mater. Sci. Eng. A 2009, 501, 197–206. [Google Scholar] [CrossRef]
- Bataillard, L.; Bidaux, J.-E.; Gotthardt, R. Interaction between microstructure and multiple-step transformation in binary NiTi alloys using in-situ transmission electron microscopy observations. Philos. Mag. A 1998, 78, 327–344. [Google Scholar] [CrossRef]
- Dlouhy, A.; Khalil-Allafi, J.; Eggeler, G. Multiple-step martensitic transformations in Ni-rich NiTi alloys—An in-situ transmission electron microscopy investigation. Philos. Mag. 2003, 83, 339–363. [Google Scholar] [CrossRef]
- Carroll, M.C.; Somsen, C.; Eggeler, G. Multiple-step martensitic transformations in Ni-rich NiTi shape memory alloys. Scr. Mater. 2004, 50, 187–192. [Google Scholar] [CrossRef]
- Khalil Allafi, J.; Ren, X.; Eggeler, G. The mechanism of multistage martensitic transformations in aged Ni-rich NiTi shape memory alloys. Acta Mater. 2002, 50, 793–803. [Google Scholar] [CrossRef]
- Karbakhsh Ravari, B.; Farjami, S.; Nishida, M. Effects of Ni concentration and aging conditions on multistage martensitic transformation in aged Ni-rich Ti–Ni alloys. Acta Mater. 2014, 69, 17–29. [Google Scholar] [CrossRef]
- Zhou, Y.; Fan, G.; Zhang, J.; Ding, X.; Ren, X.; Sun, J.; Otsuka, K. Understanding of multi-stage R-phase transformation in aged Ni-rich Ti–Ni shape memory alloys. Mater. Sci. Eng. A 2006, 438–440, 602–607. [Google Scholar] [CrossRef]
- Xue, D.; Zhou, Y.; Ren, X. The effect of aging on the B2-R transformation behaviors in Ti-51 at% Ni alloy. Intermetallics 2011, 19, 1752–1758. [Google Scholar] [CrossRef]
- Fan, G.; Chen, W.; Yang, S.; Zhu, J.; Ren, X.; Otsuka, K. Origin of abnormal multi-stage martensitic transformation behavior in aged Ni-rich Ti–Ni shape memory alloys. Acta Mater. 2004, 52, 4351–4362. [Google Scholar] [CrossRef]
- Wang, X.; Li, K.; Schryvers, D.; Verlinden, B.; Van Humbeeck, J. R-phase transition and related mechanical properties controlled by low-temperature aging treatment in a Ti-50.8 at. % Ni thin wire. Scr. Mater. 2014, 72–73, 21–24. [Google Scholar] [CrossRef]
- Wang, X.; Verlinden, B.; Van Humbeeck, J. Effect of Aging Temperature and time on the Transformation Behavior of a Ti-50.8 at. % Ni Alloy with Small Grains. Mater. Today Proc. 2015, 2, S565–S568. [Google Scholar] [CrossRef]
- Wang, X.; Li, C.; Verlinden, B.; Van Humbeeck, J. Effect of grain size on aging microstructure as reflected in the transformation behavior of a low-temperature aged Ti-50.8 at. % Ni alloy. Scr. Mater. 2013, 69, 545–548. [Google Scholar] [CrossRef]
- Khalil-Allafi, J.; Dlouhy, A.; Eggeler, G. Ni4Ti3-precipitation during aging of NiTi shape memory alloys and its influence on martensitic phase transformations. Acta Mater. 2002, 50, 4255–4274. [Google Scholar] [CrossRef]
- Johnson, W.A.; Domingue, J.A.; Reichman, S.H. P/M processing and characterization of controlled transformation temperature NiTi. J. Phys. Colloq. 1982, 43, C4-285–C4-290. [Google Scholar] [CrossRef]
- Airoldi, G.; Corsi, A.; Riva, G. The hysteresis cycle modification in thermoelastic martensitic transformation of shape memory alloys. Scr. Mater. 1997, 36, 1273–1278. [Google Scholar] [CrossRef]
- Wang, Z.; Zu, X.; Fu, Y. Review on the temperature memory effect in shape memory alloys. Int. J. Smart Nano Mater. 2011, 2, 101–119. [Google Scholar] [CrossRef]
- Resnina, N.; Belyaev, S. Multi-stage martensitic transformations induced by repeated thermal cycling of equiatomic TiNi alloy. J. Alloys Compd. 2009, 486, 304–308. [Google Scholar] [CrossRef]
- Rodríguez-Aseguinolaza, J.; Ruiz-Larrea, I.; Nó, M.L.; López-Echarri, A.; San Juan, J. A new quantitative approach to the thermoelastic martensitic transformation: The density of elastic states. Acta Mater. 2008, 56, 6283–6290. [Google Scholar] [CrossRef]
- Krishnan, M. New observations on the thermal arrest memory effect in Ni–Ti alloys. Scr. Mater. 2005, 53, 875–879. [Google Scholar] [CrossRef]
- Sun, L.; Huang, W.M.; Cheah, J.Y. The temperature memory effect and the influence of thermo-mechanical cycling in shape memory alloys. Smart Mater. Struct. 2010, 19, 055005. [Google Scholar] [CrossRef]
- Tang, W. Thermodynamic study of the low-temperature phase B19′ and the martensitic transformation in near-equiatomic Ti-Ni shape memory alloys. Metall. Mater. Trans. A 1997, 28, 537–544. [Google Scholar] [CrossRef]
- Rodríguez-Aseguinolaza, J.; Ruiz-Larrea, I.; Nó, M.L.; López-Echarri, A.; San Juan, J.M. Temperature memory effect in Cu–Al–Ni shape memory alloys studied by adiabatic calorimetry. Acta Mater. 2008, 56, 3711–3722. [Google Scholar] [CrossRef]
- Ren, X.; Miura, N.; Zhang, J.; Otsuka, K.; Tanaka, K.; Koiwa, M.; Suzuki, T.; Chumlyakov, Y.; Asai, M. A comparative study of elastic constants of Ti–Ni-based alloys prior to martensitic transformation. Mater. Sci. Eng. A 2001, 312, 196–206. [Google Scholar] [CrossRef]
- Uchil, J.; Mohanchandra, K.P.; Ganesh Kumara, K.; Mahesh, K.K.; Murali, T.P. Thermal expansion in various phases of Nitinol using TMA. Phys. B Condens. Matter 1999, 270, 289–297. [Google Scholar] [CrossRef]
- Gopal, E. Specific Heats at Low Temperatures; Springer Science & Business Media: Berlin, Germany, 2012; ISBN 978-1-4684-9081-7. [Google Scholar]
- Herget, G.; Müllner, M.; Suck, J.B.; Schmidt, R.; Wipf, H. Phonon Spectra of the Memory Alloy NiTi. EPL Europhys. Lett. 1989, 10, 49. [Google Scholar] [CrossRef]
- Birgeneau, R.J.; Cordes, J.; Dolling, G.; Woods, A.D.B. Normal Modes of Vibration in Nickel. Phys. Rev. 1964, 136, A1359–A1365. [Google Scholar] [CrossRef]
- Rudin, S.P.; Jones, M.D.; Albers, R.C. Thermal stabilization of the HCP phase in titanium. Phys. Rev. B 2004, 69, 094117. [Google Scholar] [CrossRef]
- Liu, Y.; Laeng, J.; Chin, T.V.; Nam, T.-H. Effect of incomplete thermal cycling on the transformation behaviour of NiTi. Mater. Sci. Eng. A 2006, 435–436, 251–257. [Google Scholar] [CrossRef]
- Pattabi, M.; Ramakrishna, K.; Mahesh, K.K. Corrigendum to “Effect of thermal cycling on the shape memory transformation behavior of NiTi alloy: Powder X-ray diffraction study” [Mater. Sci. Eng. A. 448 (2007) 33–38]. Mater. Sci. Eng. A 2009, 505, 191. [Google Scholar] [CrossRef]
- Karbakhsh Ravari, B.; Nishida, M. In situ SEM studies of the transformation sequence of multistage martensitic transformations in aged Ti-50.8 at. % Ni alloys. Philos. Mag. 2013, 93, 2279–2296. [Google Scholar] [CrossRef]
- Wang, X.; Kustov, S.; Li, K.; Schryvers, D.; Verlinden, B.; Van Humbeeck, J. Effect of nanoprecipitates on the transformation behavior and functional properties of a Ti-50.8 at. % Ni alloy with micron-sized grains. Acta Mater. 2015, 82, 224–233. [Google Scholar] [CrossRef]
- Wollants, P.; Roos, J.R.; Delaey, L. Thermally- and stress-induced thermoelastic martensitic transformations in the reference frame of equilibrium thermodynamics. Prog. Mater. Sci. 1993, 37, 227–288. [Google Scholar] [CrossRef]
- Rodríguez-Aseguinolaza, J.; Ruiz-Larrea, I.; Nó, M.L.; López-Echarri, A.; San Juan, J. Kinetic effects in the mixed β to martensitic transformation in a Cu–Al–Ni shape memory alloy. Acta Mater. 2010, 58, 692–701. [Google Scholar] [CrossRef]
- Rodríguez-Aseguinolaza, J.; Ruiz-Larrea, I.; Nó, M.L.; López-Echarri, A.; Bocanegra, E.H.; San Juan, J. Thermal history effects of Cu–Al–Ni shape memory alloys powder particles compared with single crystals behaviour. Intermetallics 2010, 18, 2183–2190. [Google Scholar] [CrossRef]
- Airoldi, G.; Corsi, A.; Riva, G. Step-wise martensite to austenite reversible transformation stimulated by temperature or stress: A comparison in NiTi alloys. Mater. Sci. Eng. A 1998, 241, 233–240. [Google Scholar] [CrossRef]
- He, X.M.; Rong, L.J.; Yan, D.S.; Li, Y.Y. Temperature memory effect of Ni47Ti44Nb9 wide hysteresis shape memory alloy. Scr. Mater. 2005, 53, 1411–1415. [Google Scholar] [CrossRef]












| Martensitic Transformation | Peak | Tp (°C) | MT Stages | ∆H (J/g) | ∆H (J/g) | ∆H (J/g) | ∆H (J/g) |
|---|---|---|---|---|---|---|---|
| Forward MT | 1 | 37.9 | 1 | 4.5 | 7.7 | 21.2 ± 0.6 | 21.2 ± 0.6 |
| 2 | 1.0 | 2a | 1.4 | ||||
| 3 | −16.5 | 3 | 1.8 | ||||
| 2 | 1.0 | 2b | 2.0 | 13.6 | |||
| 4 | −28.0 | 4 | 11.6 | ||||
| Reverse MT | 5 | 16.5 | 5 | 13.6 | - | 21.2 ± 0.6 | |
| 6 | 41.6 | 6 | 7.7 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ruiz-Larrea, I.; López-Echarri, A.; Breczewski, T.; López, G.A.; Lopez-Ferreño, I.; Nó, M.L.; San Juan, J.M. The Influence of Thermal History on the Multistage Transformation of NiTi Shape-Memory Alloys. Metals 2018, 8, 246. https://doi.org/10.3390/met8040246
Ruiz-Larrea I, López-Echarri A, Breczewski T, López GA, Lopez-Ferreño I, Nó ML, San Juan JM. The Influence of Thermal History on the Multistage Transformation of NiTi Shape-Memory Alloys. Metals. 2018; 8(4):246. https://doi.org/10.3390/met8040246
Chicago/Turabian StyleRuiz-Larrea, Isabel, Angel López-Echarri, Tomasz Breczewski, Gabriel A. López, Iñaki Lopez-Ferreño, María L. Nó, and Jose M. San Juan. 2018. "The Influence of Thermal History on the Multistage Transformation of NiTi Shape-Memory Alloys" Metals 8, no. 4: 246. https://doi.org/10.3390/met8040246
APA StyleRuiz-Larrea, I., López-Echarri, A., Breczewski, T., López, G. A., Lopez-Ferreño, I., Nó, M. L., & San Juan, J. M. (2018). The Influence of Thermal History on the Multistage Transformation of NiTi Shape-Memory Alloys. Metals, 8(4), 246. https://doi.org/10.3390/met8040246