Stability, Electronic Structure, and Dehydrogenation Properties of Pristine and Doped 2D MgH2 by the First Principles Study
Abstract
:1. Introduction
2. Computational Details
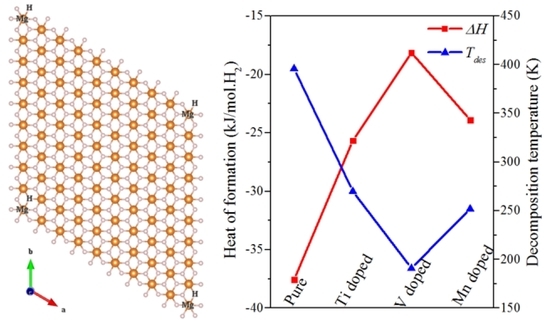
3. Results and Discussion
4. Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
Appendix A
| Hydride | PBE | LDA | ||||||
|---|---|---|---|---|---|---|---|---|
| a (Å) | α (°) | β (°) | γ (°) | a (Å) | α (°) | β (°) | γ (°) | |
| Mg9H18 | 9.033 | 90.0 | 90.0 | 120.0 | 8.894 | 90.0 | 90.0 | 120.0 |
| Mg8H18 | 9.062 | 90.0 | 90.0 | 120.0 | 8.888 | 90.0 | 90.0 | 120.0 |
| Mg8H18Ti | 9.027 | 90.0 | 90.0 | 120.0 | 8.883 | 90.0 | 90.0 | 120.0 |
| Mg8H18V | 8.951 | 90.0 | 90.0 | 120.0 | 8.803 | 90.0 | 90.0 | 120.0 |
| Mg8H18Mn | 8.815 | 90.0 | 90.0 | 120.0 | 8.662 | 90.0 | 90.0 | 120.0 |

References
- Sakintuna, B.; Lamari-Darkrim, F.; Hirscher, M. Metal hydride materials for solid hydrogen storage: A review. Int. J. Hydrogen Energy 2007, 32, 1121–1140. [Google Scholar] [CrossRef]
- Mohammed, Z.; Ahmed, R.; Mohammed Benali, K.; Bakhtiar ul, H.; Ahmad Radzi Mat, I.; Souraya, G.-S. First principle investigations of the physical properties of hydrogen-rich MgH2. Phys. Scr. 2013, 88, 065704. [Google Scholar] [CrossRef]
- Shang, C.X.; Bououdina, M.; Song, Y.; Guo, Z.X. Mechanical alloying and electronic simulations of (MgH2 + M) systems (M = Al, Ti, Fe, Ni, Cu and Nb) for hydrogen storage. Int. J. Hydrogen Energy 2004, 29, 73–80. [Google Scholar] [CrossRef]
- Ul Haq, B.; Kanoun, M.B.; Ahmed, R.; Bououdina, M.; Goumri-Said, S. Hybrid functional calculations of potential hydrogen storage material: Complex dimagnesium iron hydride. Int. J. Hydrogen Energy 2014, 39, 9709–9717. [Google Scholar] [CrossRef]
- Kumar, D.; Singh, A.; Prasad Tiwari, G.; Kojima, Y.; Kain, V. Thermodynamics and kinetics of nano-engineered Mg-MgH2 system for reversible hydrogen storage application. Thermochim. Acta 2017, 652, 103–108. [Google Scholar] [CrossRef]
- Trivedi, D.R.; Bandyopadhyay, D. Study of adsorption and dissociation process of H2 molecule on MgnRh clusters: A density functional investigation. Int. J. Hydrogen Energy 2016, 41, 20113–20121. [Google Scholar] [CrossRef]
- Song, Y.; Guo, Z.X.; Yang, R. Influence of selected alloying elements on the stability of magnesium dihydride for hydrogen storage applications: A first-principles investigation. Phys. Rev. B 2004, 69, 094205. [Google Scholar] [CrossRef]
- Vajeeston, P.; Ravindran, P.; Kjekshus, A.; Fjellvåg, H. Pressure-Induced Structural Transitions in MgH2. Phys. Rev. Lett. 2002, 89, 175506. [Google Scholar] [CrossRef] [PubMed]
- Kurko, S.; Matović, L.; Novaković, N.; Matović, B.; Jovanović, Z.; Mamula, B.P.; Grbović Novaković, J. Changes of hydrogen storage properties of MgH2 induced by boron ion irradiation. Int. J. Hydrogen Energy 2011, 36, 1184–1189. [Google Scholar] [CrossRef]
- Song, M.Y.; Kwon, S.N.; Park, H.R.; Hong, S.-H. Improvement in the hydrogen storage properties of Mg by mechanical grinding with Ni, Fe and V under H2 atmosphere. Int. J. Hydrogen Energy 2011, 36, 13587–13594. [Google Scholar] [CrossRef]
- Noritake, T.; Aoki, M.; Towata, S.; Seno, Y.; Hirose, Y.; Nishibori, E.; Takata, M.; Sakata, M. Chemical bonding of hydrogen in MgH2. Appl. Phys. Lett. 2002, 81, 2008–2010. [Google Scholar] [CrossRef]
- Liang, G.; Huot, J.; Boily, S.; Van Neste, A.; Schulz, R. Catalytic effect of transition metals on hydrogen sorption in nanocrystalline ball milled MgH2 − Tm (Tm = Ti, V, Mn, Fe and Ni) systems. J. Alloys Compd. 1999, 292, 247–252. [Google Scholar] [CrossRef]
- Shang, C.X.; Bououdina, M.; Guo, Z.X. Structural stability of mechanically alloyed (Mg + 10Nb) and (MgH2 + 10Nb) powder mixtures. J. Alloys Compd. 2003, 349, 217–223. [Google Scholar] [CrossRef]
- Rivoirard, S.; de Rango, P.; Fruchart, D.; Charbonnier, J.; Vempaire, D. Catalytic effect of additives on the hydrogen absorption properties of nano-crystalline MgH2(X) composites. J. Alloys Compd. 2003, 356, 622–625. [Google Scholar] [CrossRef]
- Oelerich, W.; Klassen, T.; Bormann, R. Metal oxides as catalysts for improved hydrogen sorption in nanocrystalline Mg-based materials. J. Alloys Compd. 2001, 315, 237–242. [Google Scholar] [CrossRef]
- Aguey-Zinsou, K.F.; Ares Fernandez, J.R.; Klassen, T.; Bormann, R. Effect of Nb2O5 on MgH2 properties during mechanical milling. Int. J. Hydrogen Energy 2007, 32, 2400–2407. [Google Scholar] [CrossRef]
- Song, M.; Bobet, J.-L.; Darriet, B. Improvement in hydrogen sorption properties of Mg by reactive mechanical grinding with Cr2O3, Al2O3 and CeO2. J. Alloys Compd. 2002, 340, 256–262. [Google Scholar] [CrossRef]
- Kresse, G.; Furthmüller, J. Efficient Iterative Schemes for Ab Initio Total-Energy Calculations Using a Plane-Wave Basis Set. Phys. Rev. B Condens. Matter 1996, 54, 11169–11186. [Google Scholar] [CrossRef] [PubMed]
- Kresse, G.; Joubert, D. From ultrasoft pseudopotentials to the projector augmented-wave method. Phys. Rev. B 1999, 59, 1758–1775. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef] [PubMed]
- Hammer, B.; Hansen, L.B.; Nørskov, J.K. Improved adsorption energetics within density-functional theory using revised Perdew-Burke-Ernzerhof functionals. Phys. Rev. B 1999, 59, 7413–7421. [Google Scholar] [CrossRef] [Green Version]
- Monkhorst, H.J.; Pack, J.D. Special points for Brillouin-zone integrations. Phys. Rev. B 1976, 13, 5188–5192. [Google Scholar] [CrossRef]
- Perdew, J.P.; Zunger, A. Self-interaction correction to density-functional approximations for many-electron systems. Phys. Rev. B 1981, 23, 5048–5079. [Google Scholar] [CrossRef]
- Heyd, J.; Scuseria, G.E.; Ernzerhof, M. Erratum: Hybrid functionals based on a screened Coulomb potential. J. Chem. Phys. 2006, 118, 8207. [Google Scholar] [CrossRef]
- Togo, A.; Oba, F.; Tanaka, I. First-Principles Calculations of the Ferroelastic Transition Between Rutile-Type and CaCl2-Type SiO2 at High Pressures. Phys. Rev. B Condens. Matter 2008, 78. [Google Scholar] [CrossRef]
- Gonze, X.; Lee, C. Dynamical matrices, Born effective charges, dielectric permittivity tensors, and interatomic force constants from density-functional perturbation theory. Phys. Rev. B 1997, 55, 10355–10368. [Google Scholar] [CrossRef]
- Baroni, S.; de Gironcoli, S.; Dal Corso, A.; Giannozzi, P. Phonons and related crystal properties from density-functional perturbation theory. Rev. Mod. Phys. 2001, 73, 515–562. [Google Scholar] [CrossRef] [Green Version]
- Gu, T.; Wang, Z.; Tada, T.; Watanabe, S. First-principles simulations on bulk Ta2O5 and Cu/Ta2O5/Pt heterojunction: Electronic structures and transport properties. J. Appl. Phys. 2009, 106, 262907. [Google Scholar] [CrossRef]
- Sun, R.; Wang, Z.; Saito, M.; Shibata, N.; Ikuhara, Y. Atomistic mechanisms of nonstoichiometry-induced twin boundary structural transformation in titanium dioxide. Nat. Commun. 2011, 6, 7120. [Google Scholar] [CrossRef] [PubMed]
- Wang, Z.; Saito, M.; Mckenna, K.P.; Gu, L.; Tsukimoto, S.; Shluger, A.L.; Ikuhara, Y. Atom-resolved imaging of ordered defect superstructures at individual grain boundaries. Nature 2011, 479, 380–383. [Google Scholar] [CrossRef] [PubMed]
- McKenna, K.P.; Hofer, F.; Gilks, D.; Lazarov, V.K.; Chen, C.; Wang, Z.; Ikuhara, Y. Atomic-scale structure and properties of highly stable antiphase boundary defects in Fe3O4. Nat. Commun. 2014, 5, 5740. [Google Scholar] [CrossRef] [PubMed]
- Wang, Z.; Saito, M.; Mckenna, K.P.; Fukami, S.; Sato, H.; Ikeda, S.; Ohno, H.; Ikuhara, Y. Atomic-Scale Structure and Local Chemistry of CoFeB-MgO Magnetic Tunnel Junctions. Nano Lett. 2016, 16, 1530–1536. [Google Scholar] [CrossRef] [PubMed]
- Yan, H.; Ziyu, H.; Xu, G.; Xiaohong, S. Structural, electronic and photocatalytic properties of atomic defective BiI3 monolayers. Chem. Phys. Lett. 2018, 691, 341–346. [Google Scholar] [CrossRef]
- García, G.N.; Abriata, J.P.; Sofo, J.O. Calculation of the electronic and structural properties of cubic Mg2NiH4. Phys. Rev. B 1999, 59, 11746–11754. [Google Scholar] [CrossRef]
- Chen, Y.; Dai, J.; Xie, R.; Song, Y.; Bououdina, M. First principles study of dehydrogenation properties of alkali/alkali-earth metal doped Mg7TiH16. J. Alloys Compd. 2017, 728, 1016–1022. [Google Scholar] [CrossRef]
- Shelyapina, M.G.; Fruchart, D.; Wolfers, P. Electronic structure and stability of new FCC magnesium hydrides Mg7MH16 and Mg6MH16 (M = Ti, V, Nb): An ab initio study. Int. J. Hydrogen Energy 2010, 35, 2025–2032. [Google Scholar] [CrossRef]
- Dai, J.H.; Song, Y.; Yang, R. First Principles Study on Hydrogen Desorption from a Metal (=Al, Ti, Mn, Ni) Doped MgH2 (110) Surface. J. Phys. Chem. C 2010, 114, 11328–11334. [Google Scholar] [CrossRef]
- Kumar, M.; Kamal, R.; Thapa, R. Screening based approach and dehydrogenation kinetics for MgH2: Guide to find suitable dopant using first-principles approach OPEN. Sci. Rep. 2017, 7, 15550. [Google Scholar] [CrossRef] [PubMed]
- Van Mal, H.H.; Buschow, K.H.J.; Miedema, A.R. Hydrogen absorption in LaNi5 and related compounds: Experimental observations and their explanation. J. Less Common Met. 1974, 35, 65–76. [Google Scholar] [CrossRef]
- Lakhal, M.; Bhihi, M.; Benyoussef, A.; El Kenz, A.; Loulidi, M.; Naji, S. The hydrogen ab/desorption kinetic properties of doped magnesium hydride MgH2 systems by first principles calculations and kinetic Monte Carlo simulations. Int. J. Hydrogen Energy 2015, 40, 6137–6144. [Google Scholar] [CrossRef]
- Alapati, S.V.; Johnson, J.K.; Sholl, D.S. Identification of Destabilized Metal Hydrides for Hydrogen Storage Using First Principles Calculations. J. Phys. Chem. B 2006, 110, 8769–8776. [Google Scholar] [CrossRef] [PubMed]
- Yu, R.; Lam, P.K. Electronic and structural properties of MgH2. Phys. Rev. B 1988, 37, 8730–8737. [Google Scholar] [CrossRef]
- Westerwaal, R.J.; Broedersz, C.P.; Gremaud, R.; Slaman, M.; Borgschulte, A.; Lohstroh, W.; Tschersich, K.G.; Fleischhauer, H.P.; Dam, B.; Griessen, R. Study of the hydride forming process of in-situ grown MgH2 thin films by activated reactive evaporation. Thin Solid Films 2008, 516, 4351–4359. [Google Scholar] [CrossRef]





| Lattice Parameters | Atom | Wyckoff | Atomic Positions (Fractional) | ||
|---|---|---|---|---|---|
| Positions | x | y | z | ||
| 164(P-3m1) | Mg1 | 1b | 0 | 0 | 0.5 |
| a = b = 9.033 Å | Mg2 | 6h | 0 | 0.33333 | 0.5 |
| c = 15 Å | Mg3 | 2d | 0.33333 | 0.66667 | 0.5 |
| d = 1.86 Å | H1 | 6i | 0.11111 | 0.22222 | 0.43783 |
| α = β = 90° | H2 | 6i | 0.22222 | 0.44444 | 0.56217 |
| γ = 120° | H3 | 6i | 0.11111 | 0.55556 | 0.43783 |
| Hydride | ΔE (eV) | Parameter | Bond Length (Å) | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Mg1 | Mg2 | Mg3 | a (Å) | Sub-H1 | Mg2-H1 | Mg2-H2 | Mg2-H3 | Mg3-H2 | Mg3-H3 | |
| Mg9H18 | 0 | 0 | 0 | 9.033 | 1.972 | 1.972 | 1.972 | 1.972 | 1.972 | 1.972 |
| Mg8H18 | 2.968 | 2.968 | 2.968 | 9.062 | - | 1.894 | 2.043 | 1.976 | 1.947 | 1.992 |
| Mg8H18Ti | 1.113 | 1.114 | 1.114 | 9.027 | 1.915 | 1.997 | 1.964 | 1.982 | 1.946 | 1.990 |
| Mg8H18V | 1.818 | 1.818 | 1.819 | 8.951 | 1.822 | 1.999 | 1.945 | 1.992 | 1.939 | 1.983 |
| Mg8H18Mn | 1.279 | 1.279 | 1.279 | 8.815 | 1.691 | 2.028 | 1.911 | 2.008 | 1.937 | 1.965 |
| Hydride | ΔH | T | Bader Charge (e) | Ed | ||
|---|---|---|---|---|---|---|
| (kJ/mol·H2) | (K) | Mg | X | H | (eV) | |
| Mg9H18 | −37.57 | 268~396 | +2.000 | - | −0.997 | 1.589 |
| Mg8H18 | 31.71 | - | +2.000 | - | −0.886 | −1.931 |
| Mg8H18Ti | −25.67 | 183~270 | +2.000 | +1.825 | −0.988 | 1.305 |
| Mg8H18V | −18.14 | 130~191 | +2.000 | +1.523 | −0.971 | 1.044 |
| Mg8H18Mn | −23.90 | 171~252 | +2.000 | +0.975 | −0.940 | 0.853 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gong, X.; Shao, X. Stability, Electronic Structure, and Dehydrogenation Properties of Pristine and Doped 2D MgH2 by the First Principles Study. Metals 2018, 8, 482. https://doi.org/10.3390/met8070482
Gong X, Shao X. Stability, Electronic Structure, and Dehydrogenation Properties of Pristine and Doped 2D MgH2 by the First Principles Study. Metals. 2018; 8(7):482. https://doi.org/10.3390/met8070482
Chicago/Turabian StyleGong, Xu, and Xiaohong Shao. 2018. "Stability, Electronic Structure, and Dehydrogenation Properties of Pristine and Doped 2D MgH2 by the First Principles Study" Metals 8, no. 7: 482. https://doi.org/10.3390/met8070482
APA StyleGong, X., & Shao, X. (2018). Stability, Electronic Structure, and Dehydrogenation Properties of Pristine and Doped 2D MgH2 by the First Principles Study. Metals, 8(7), 482. https://doi.org/10.3390/met8070482