Experimental Investigation on the Response of Elliptical CFT Columns Subjected to Lateral Impact Loading
Abstract
:1. Introduction
2. Experimental Program
2.1. Test Specimens
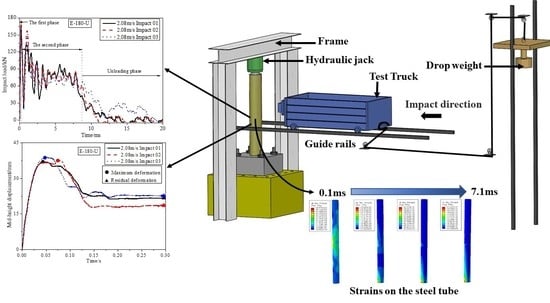
2.2. The Horizontal-Impact-Testing System
2.3. Data Measuring Instrumentation
2.4. Test Setup
3. Experimental Results and Discussion
3.1. Test Observations
3.2. Impact Load-Time History
3.3. Displacement Time Histories
3.4. Strain and Strain Rates
3.5. Energy Absorption
4. Finite Element Modeling
4.1. Finite Element Model
4.2. Verifications of the FEA Model
4.3. Strain Mechanism Analysis
- (1)
- Local response: In this state, when the test truck made contact with the specimen, the stress rapidly increased at the impact location. Also, slight damage of steel tube and core concrete was obtained at the impact location. The stress wave, produced by the impact, spread to the two ends of the column. At the same time, the impact force rapidly increased from zero to the peak value and the deformation was almost zero. This shows that the impact force was basically balanced by the inertial force. At the same location, the strain on the concrete was larger than that on the steel tube. This indicates that the slip occurred between the steel tube and the concrete. Thus, the deformation coordination condition was not satisfied;
- (2)
- Overall response: After the peak load, the specimen showed its overall response. The strain gradually increased at the bottom of the column. In this stage, the stress wave travelled through the whole specimen. The strain of the specimen dramatically increased; meanwhile, the damage extended at the impact location;
- (3)
- Stable response: In this stage, the impact force generally remained stable; however, the kinetic energy of test truck was converted into internal energy of the specimen, and the deformation increased. Thus, the strains of steel tube and core concrete developed further. The plastic region at the bottom of specimen continued to expand;
- (4)
- Descending response: In this stage, the impact force decreased to zero. This indicates that the test truck separated with the specimen and they reversed their velocity direction. Then, the specimen reached the maximum displacement. At last, the deflection of the specimen stayed at the residual deformation with the vibration. The plastic region of the concrete was larger than that of the steel tube.
5. Conclusions
- (1)
- Under the lateral impact load, the elliptical CFT columns had good impact performance. The columns had global deformations with noticeable outward buckling of the steel tubes;
- (2)
- The impact load-time histories can be divided into three phases. The first impact force was mainly governed by the impact velocity within about 0.2 ms. Under the same impact velocity, the first peak impact load increased and then decreased due to the increased times of impact. A second peak force was obtained at the same velocity acquired by the specimen and test truck. The test truck and the specimen separated following the unloading phase;
- (3)
- The elliptical CFT columns have good ductility under an impact load with higher displacements. The displacement at the column top was almost twice the value at the mid-height but with a delay;
- (4)
- The strains and strain rates descended in half-sine waveforms after reaching the maximum values. The strain rates in this study were small as the impact velocities were small. The elliptical CFT columns dissipated almost the same energy under the same impact velocity, and more energy was dissipated with the increased impact velocity;
- (5)
- The dynamic responses of elliptical CFT columns under lateral impact loading can be simulated by establishing the finite element model. The mechanical mechanism of the strains can be divided into four stages. The stress wave travelled through the whole specimen at the overall response, while the strain was obtained at the impact location during the local response. The strains developed more extensively during the stable responses. Also, the vibrations of the specimens occurred during the descending responses.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Deng, L.; Wang, W.; Yu, Y. State-of-the-art review on the causes and mechanisms of bridge collapse. J. Perform. Constr. Facil. 2016, 30, 4015005. [Google Scholar] [CrossRef]
- El-Tawil, S.; Severino, E.; Fonseca, P. Vehicle collision with bridge piers. J. Bridge Eng. 2005, 10, 345–353. [Google Scholar] [CrossRef] [Green Version]
- Espinos, A.; Romero, M.L.; Serra, E.; Hospitaler, A. Circular and square slender concrete-filled tubular columns under large eccentricities and fire. J. Constr. Steel Res. 2015, 110, 90–100. [Google Scholar] [CrossRef]
- Han, L.H.; Li, W.; Bjorhovde, R. Developments and advanced applications of concrete-filled steel tubular (CFST) structures: Members. J. Constr. Steel Res. 2014, 100, 211–228. [Google Scholar] [CrossRef]
- Uy, B. Stability and ductility of high performance steel sections with concrete infill. J. Constr. Steel Res. 2008, 64, 748–754. [Google Scholar] [CrossRef]
- Naghipour, M.; Yousofizinsaz, G.; Shariati, M. Experimental study on axial compressive behavior of welded built-up CFT stub columns made by cold-formed sections with different welding lines. Steel Compos. Struct. 2020, 34, 347–359. [Google Scholar]
- Liao, J.J.; Zeng, J.J.; Long, Y.L.; Cai, J.; Yi, O.Y. Behavior of square and rectangular concrete-filled steel tube (CFST) columns with horizontal reinforcing bars under eccentric compression. Eng. Struct. 2022, 271, 114899. [Google Scholar] [CrossRef]
- Zhao, X.L.; Packer, J.A. Tests and design of concrete-filled elliptical hollow section stub columns. Thin-Walled Struct. 2009, 47, 617–628. [Google Scholar] [CrossRef]
- Yang, H.; Lam, D.; Gardner, L. Testing and analysis of concrete-filled elliptical hollow sections. Eng. Struct. 2008, 30, 3771–3781. [Google Scholar] [CrossRef]
- Mahgub, M.; Ashour, A.; Lam, D.; Dai, X. Tests of self-compacting concrete filled elliptical steel tube columns. Thin-Walled Struct. 2017, 110, 27–34. [Google Scholar] [CrossRef] [Green Version]
- Cai, Y.; Quach, W.; Young, B. Experimental and numerical investigation of concrete-filled hot-finished and cold-formed steel elliptical tubular stub columns. Thin-Walled Struct. 2019, 145, 106437. [Google Scholar] [CrossRef]
- Ipek, S.; Erdoğan, A.; Güneyisi, E.M. Compressive behavior of concrete-filled double skin steel tubular short columns with the elliptical hollow section. J. Build. Eng. 2021, 38, 102200. [Google Scholar] [CrossRef]
- Long, Y.L.; Zeng, L. A refined model for local buckling of rectangular CFST columns with binding bars. Thin-Walled Struct. 2018, 132, 431–441. [Google Scholar] [CrossRef]
- Long, Y.L.; Zeng, L.; Gardner, L.; Wadee, M.A. A new model for calculating the elastic local buckling stress of steel plates in square CFST columns. Thin-Walled Struct. 2022, 171, 108756. [Google Scholar] [CrossRef]
- Banthia, N.; Mindess, S.; Bentur, A.; Pigeon, M. Impact testing of concrete using a drop-weight impact machine. Exp. Mech. 1989, 29, 63–69. [Google Scholar] [CrossRef]
- Remennikov, A.M.; Kong, S.Y.; Uy, B. Response of foam- and concrete-filled square steel tubes under low-velocity impact loading. J. Perform. Constr. Facil. 2011, 25, 373–381. [Google Scholar] [CrossRef]
- Wang, R.; Han, L.H.; Hou, C.C. Behavior of concrete filled steel tubular (CFST) members under lateral impact: Experiment and FEA model. J. Constr. Steel Res. 2013, 80, 188–201. [Google Scholar] [CrossRef]
- Yousuf, M.; Uy, B.; Tao, Z.; Remennikov, A.; Liew, J.Y.B. Impact behaviour of pre-compressed hollow and concrete filled mild and stainless steel columns. J. Constr. Steel Res. 2014, 96, 54–68. [Google Scholar] [CrossRef]
- Yang, Y.; Zhang, Z.; Fu, F. Experimental and numerical study on square RACFST members under lateral impact loading. J. Constr. Steel Res. 2015, 111, 43–56. [Google Scholar] [CrossRef] [Green Version]
- Chen, L.; Wu, H.; Fang, Q.; Li, R.W. Full-scale experimental study of a reinforced concrete bridge pier under truck collision. J. Bridge Eng. 2021, 26, 05021008. [Google Scholar] [CrossRef]
- Aghdamy, S.; Thambiratnam, D.P.; Dhanasekar, M. Experimental investigation on lateral impact response of concrete-filled double-skin tube columns using horizontal-impact-testing system. Exp. Mech. 2016, 56, 1133–1153. [Google Scholar] [CrossRef]
- Sha, Y.; Hao, H. Laboratory tests and numerical simulations of barge impact on circular reinforced concrete piers. Eng. Struct. 2013, 46, 593–605. [Google Scholar] [CrossRef]
- Zhang, X.H.; Hao, H.; Li, C. Experimental investigation of the response of precast segmental columns subjected to impact loading. Int. J. Impact Eng. 2016, 95, 105–124. [Google Scholar] [CrossRef] [Green Version]
- Feng, Z.J.; Wang, X.l.; Zhang, S.F.; Chu, Y.P. Experimental investigation on cantilever square CFST columns under lateral continuous impact loads. J. Constr. Steel Res. 2022, 196, 107416. [Google Scholar] [CrossRef]
- Demartino, C.; Wu, J.G.; Xiao, Y. Response of shear-deficient reinforced circular RC columns under lateral impact loading. Int. J. Impact Eng. 2017, 109, 196–213. [Google Scholar] [CrossRef]
- Ye, J.B.; Wang, Y.T.; Cai, J.; Chen, Q.J.; He, A. Evaluation of residual lateral capacities of impact-damaged reinforced concrete members. Buildings 2022, 12, 669. [Google Scholar] [CrossRef]
- Batarlar, B.; Hering, M.; Bracklow, F.; Kühn, T.; Beckmann, B.; Curbach, M. Experimental investigation on reinforced concrete slabs strengthened with carbon textiles under repeated impact loads. Struct. Concr. 2021, 22, 120–131. [Google Scholar] [CrossRef]
- Abdallah, M.H.; Hajiloo, H.; Braimah, A. Structural response of circular concrete columns confined with gfrp tubes under repeated and sequential impact loads. SSRN 2022, 7, 4159300. [Google Scholar] [CrossRef]
- Kadhim, M.M.A.; Semendary, A.A.; Hammed, M.; Cunningham, L.S. Numerical investigation of hybrid UHPC columns subject to lateral impact. J. Bridge Eng. 2022, 47, 103914. [Google Scholar] [CrossRef]

















| Specimens | D/B/t/L mm | fc/ mPa | fy/ mPa | fu/ mPa | N/ kN | Impact Direction |
|---|---|---|---|---|---|---|
| E-120-I | 180/120/6/2200 | 29.62 | 331.6 | 480.9 | 184 | along the minor axis |
| E-120-U | 180/120/6/2200 | 29.62 | 331.6 | 480.9 | 184 | along the minor axis |
| E-180-I | 180/120/6/2200 | 29.62 | 331.6 | 480.9 | 184 | along the major axis |
| E-180-U | 180/120/6/2200 | 29.62 | 331.6 | 480.9 | 184 | along the major axis |
| C-180-I | 180/180/6/2200 | 29.62 | 331.6 | 480.9 | 251 | along the major axis |
| Specimens | Impact Velocity m/s | PIF /kN | Time /ms | It/ kN·ms | Maximum Deformation /mm | Residual Deformation /mm | Energy Dissipation /J |
|---|---|---|---|---|---|---|---|
| E-120-I | 2.31 | 141.2 | 6.5 | 437 | 34.08 | 16.59 | 2131 |
| 2.71 | 166.9 | 7.1 | 488 | 41.42 | 18.60 | 3075 | |
| 3.12 | 198.4 | 7.3 | 531 | 48.94 | 23.74 | 4011 | |
| E-120-U | 1.20 | 103.3 | 12.2 | 419 | 19.64 | 4.99 | 1035 |
| 1.20 | 107.4 | 12.1 | 449 | 22.01 | 6.73 | 1223 | |
| 1.20 | 104.0 | 12.6 | 421 | 22.03 | 9.23 | 1222 | |
| 1.20 | 104.7 | 13.5 | 423 | 21.78 | 9.34 | 1239 | |
| 1.20 | 101.5 | 10.6 | 412 | 21.60 | 10.02 | 1223 | |
| E-180-I | 1.31 | 137.5 | 9.3 | 649 | 22.44 | 15.27 | 1795 |
| 1.77 | 175.5 | 10.5 | 748 | 39.73 | 22.91 | 3282 | |
| 2.04 | 226.0 | 11.6 | 869 | 46.88 | 26.00 | 4536 | |
| 2.34 | 240.4 | 16.3 | 1212 | 54.28 | 29.92 | 5528 | |
| E-180-U | 2.08 | 168.1 | 13.1 | 752 | 36.98 | 22.46 | 3120 |
| 2.08 | 174.9 | 10.9 | 755 | 37.57 | 19.19 | 3192 | |
| 2.08 | 161.7 | 11.8 | 774 | 38.84 | 22.63 | 3082 | |
| C-180-I | 1.8 | 209.5 | 9.3 | 875 | 17.49 | 0.32 | 1878 |
| 2.36 | 272.5 | 9.3 | 965 | 23.58 | 6.05 | 3044 | |
| 2.8 | 339.8 | 9.9 | 1058 | 30.51 | 18.61 | 4754 | |
| 3.19 | 357.8 | 8.3 | 1008 | 39.90 | 26.73 | 6273 | |
| 3.5 | 373.8 | 9.3 | 1082 | 48.54 | 23.68 | 7597 | |
| 3.88 | 407.3 | 15.3 | 1464 | 55.57 | 28.72 | 9198 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Y.; Hu, S. Experimental Investigation on the Response of Elliptical CFT Columns Subjected to Lateral Impact Loading. Buildings 2022, 12, 1847. https://doi.org/10.3390/buildings12111847
Wang Y, Hu S. Experimental Investigation on the Response of Elliptical CFT Columns Subjected to Lateral Impact Loading. Buildings. 2022; 12(11):1847. https://doi.org/10.3390/buildings12111847
Chicago/Turabian StyleWang, Yingtao, and Shaohua Hu. 2022. "Experimental Investigation on the Response of Elliptical CFT Columns Subjected to Lateral Impact Loading" Buildings 12, no. 11: 1847. https://doi.org/10.3390/buildings12111847
APA StyleWang, Y., & Hu, S. (2022). Experimental Investigation on the Response of Elliptical CFT Columns Subjected to Lateral Impact Loading. Buildings, 12(11), 1847. https://doi.org/10.3390/buildings12111847