3.1. Data Fitting for Marginal Distributions under Incomplete Information
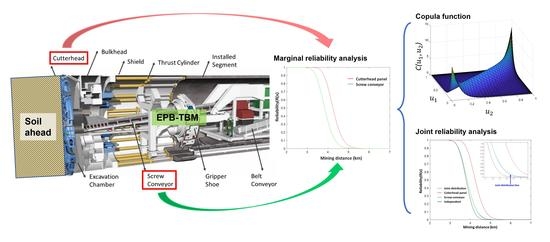
The data used in this research mainly include the remaining thickness for the wear-resistant material on the TBM’s key components, namely the cutter head panel and screw conveyor. In particular, the remaining thickness of the wear-resistance strip welded on the different sides of the cutter head panel was measured prior to and during tunnel excavation. The cutter head panel was evenly divided into several zones, with a few locations measured for each zone. To avoid data bias, the average value for each zone was calculated to represent the zone. Similarly, the screw conveyor was divided into several zones and the remaining thickness of the wear-resistance strips was measured at the same location as the cutter head panels. The collected data were used to analyze the service life of single components as well as the joint distribution of the overall service life prediction.
The marginal distribution functions describe the reliability of TBM components with respect to mining distance. To establish the copula model on the TBM lifetime prediction, it was critical to derive the marginal distribution function for all key components involved. However, the data obtained from the site were incomplete due to the limited site measurements available. To overcome this problem, a marginal distribution function with incomplete information was constructed by the following steps.
Figure 1.
Flowchart of the developed approach for reliability assessment in complex systems.
Figure 1.
Flowchart of the developed approach for reliability assessment in complex systems.
Step 1: We defined the remaining thickness of wear-resistance structures in the cutter head panel and screw conveyor over the mining distance
following a function
. In this function,
i indicates the type of components (
i = 1 for cutter head panel,
i = 2 for screw conveyor). In this research, we assumed that the relationship between the mining distance and the remaining thickness for the cutter head panel or the screw conveyor was linear. This assumption was purely based on the observation of the data, and it might not be applicable to other cases. A different function can be proposed based on the nature of the collected data or estimated by means of the maximum likelihood methods [
51]. In this study, the function was proposed as follows.
where
α indicates the initial thickness,
β is the rate of wearing, and
x is the mining distance. The normal distribution, Weibull distribution, Gumbel distribution, and logistics distribution were selected as candidate marginal distributions to describe the relationship between the remaining distance of the wear-resistance structure and the mining distance.
Step 2: For the normal distribution, i.e.,
,
,
follows Equation (1). As
α and
β are independent, the mean and variance for function
can be expressed as follows:
where parameters from Equations (2) and (3) can be derived by finding out the best-fitting distribution based on TBM mining data.
Step 3: The function
was defined as the probability of the component malfunction, and the malfunction value for the cutter head panel and screw conveyor was set as
and
. If the thickness of the wear-resistance structure for these two components falls below the malfunction value,
, then the TBM is considered unreliable for work. Therefore, the function
is the cumulative density function (CDF) of
, and it is expressed as follows:
where
and
denote the expression in the bracket that follows the CDF of standard normal distribution.
Step 4: The function
was defined as the probability of component functions reliability. The probability for the component is 1 when the tunneling work just starts and gradually reduces with the increment of mining distance. That is,
reduces and
increases as the mining distance
increases. However, the total probability of component reliability and malfunction is always constant. Therefore,
, and
is expressed as
Step 5: The same procedure is repeated in steps 2–4 for the Weibull distribution and/or Gumbel distribution. However, the mean
and variance
for the normal distribution is replaced by the location parameter
and scale parameter
for the Gumbel distribution, the shape parameter
and scale parameter
for the Weibull distribution, and the location parameter
and scale parameter
for logistic distribution. The reliability function for the Gumbel distribution, Weibull distribution, and logistic distribution can be expressed in Equations (6)–(8), respectively:
where the location parameter
and scale parameter
for the Gumbel distribution, shape factor
, the scale parameter
for the Weibull distribution, and location parameter
and scale parameter
for the logistics distribution.
Step 6: The goodness of fit for candidate distributions should be estimated to determine the best fitting type of marginal distribution. Akaike Information Criteria (AIC) [
52] and Bayesian Information Criteria (BIC) [
53] are the two common measures for checking data fitness.
AIC and
BIC are estimators that can estimate the quality of each model, which is the best-fitting marginal distribution function.
AIC and
BIC values can be calculated based on the formulas below:
where
k is the number of correlation parameters in the model,
N is the number of data, and
is the maximum value of the likelihood function of the model. As Equations (9) and (10) suggest, the difference between
AIC and
BIC is that
BIC gives more penalty when a greater number of correlation parameters are involved in the model under relatively big data size. However, as the parameters in candidate models are the same in this case,
AIC and
BIC values should be consistent. Therefore, the model should be selected when
AIC and
BIC values are the lowest among the candidate models.
3.2. Structural Learning for System Failure Models
The structure of the failure mode is critical for reliability analysis. The failure structure of the system is determined according to the mechanism and the relation between the components. Generally, serial, parallel, and mixed are the three essential relationships between the components in an engineering system [
54]. If the components are in serial, the system will fail if any of its components fail. For a parallel system, the system will succeed if any of its components succeed. The mixed system is a more complicated system that contains both serial and parallel systems [
55]. One of the useful tools to describe the relationship between the components and the overall system is the reliability block diagram (RBD) method. In this approach, the influential components are represented by blocks, and their relationships are denoted by the links in between. Given components 1, 2, …,
i, and their marginal failure probability functions
,
, …,
, the joint failure probability is different if the components are constructed in different structures.
For a system that consists of two components, their relationship would be either serial or parallel.
Figure 2 summarizes the RBD for a system with two components. The system follows failure mode (a) if the two components are in parallel and mode (b) if the two components are in serial. Apart from different failure modes, the dependency between each component affects the joint probability as well. For example, if the given system follows mode (a) and the two sub-systems are independent of each other, the reliability can be calculated as
. However, if the two sub-systems are dependent, the reliability is calculated as
, where
C denotes the copula function, and
is the correlation parameter between the two marginal variables. Similarly, the general formula of the reliability function
under different failure mode structures and different dependency conditions (dependent or independent) can be calculated, respectively, and the results are shown in
Table 2.
For the system that consists of three components, the relationship can be serial, parallel, or mixed.
Figure 3 summarizes the RBD for a system with three components. Similar to the two component case, mode (a) and (b) describe the failure scenarios for the three component system, where mode (a) is for all components in parallel and mode (b) is for all in serial. However, there are three other possible failure modes described in (c), (d), and (e), where the components are in a mixed system. Different RBDs are formed based on the different critical paths of the components. Mode (c) is followed when two components (
) are replaceable with each other while any of them can form a critical path with the other one (
). However, if there are two possible critical paths between the two components (
) or
, mode (d) is followed. If the system can properly function when any two out of three components are working well, mode (e) describes such a situation. The reliability functions
for three components under different failure modes and dependencies are also summarized in
Table 2. For instance, if a system has three components, then a failure of all causes the system to break down. In this case, these three components are in parallel and failure mode (a) in
Table 2 is followed. As a result, the reliability function follows
.
3.3. Copula Enabled Data-Driven Prediction
Copulas are functions that describe the dependency between the
n-dimensional multivariate joint distribution and
1-dimensional marginal functions, given that the probability distribution of these variables is uniform [
56]. Derived by Sklar [
57], given a d-dimensional CDF,
, with marginal functions
, a copula
C exists, as shown below:
where all
and
. The copula function is unique if
is continuous for all
. For the case of two variables, the formula can be rewritten as follows.
where
C denotes the copula function,
is the correlation parameter between the two marginal variables, and
refer to the marginal distribution functions for
, respectively. Therefore, the copula function is utilized to develop the reliability function model that includes dependent marginal variables.
There are three types of copula functions largely applied in engineering studies, namely Archimedean copulas, Elliptical copulas, and Vine copulas. Archimedean copulas are by far the most popular copulas due to their relatively simple structure, ease of calculation, and high adaptability and flexibility in engineering problems [
58]. Therefore, Archimedean copulas were tested in this paper to find the most suitable copula type for the TBM service life prediction model. The selected candidate copulas are shown in
Table 3 below.
Before the confirmation of the copula function, it is vital to analyze the dependence structure of copulas. There are three principles used to measure the dependence: Pearson correlation, rank correlation, and coefficient of tail dependence. Pearson correlation mainly measures the linear relationship between variables, while it is not suitable for non-linear conditions. Spearman’s rho and Kendall’s tau are the key values for rank correlation measures, and they are very useful in calibrating copula functions. Tail dependence was not necessary to be measured in this case. Therefore, Kendall’s tau was utilized to measure the dependence and correlation parameter
θ. For two random variables
and
, Kendall’s tau
is defined as
where
is defined as
Based on the copula theory, the correlation parameter of copula
θ can be calculated based on the following equation:
AIC and
BIC are used to determine the best-fitting candidate copula models.
AIC and
BIC values for the copula model can be calculated based on the formula below.
where
denotes the likelihood function and can be regarded as the density of the respective copula function, where
[
59,
60].
AIC and
BIC values are calculated for each candidate copula function, and the one with the minimum
AIC and
BIC values is the best-fit model among the candidate copula models.
From
Section 3.1, the remaining lifetime function for a single component is
. Therefore, with the copula model developed in
Section 3.2, the remaining lifetime function of the whole TBM can be expressed as below.
where
,
are the marginal distribution function for the remaining lifetime of the wear-resistance structure in the cutter head panel and screw conveyor, respectively.
is the copula function that indicates the probability of both components.