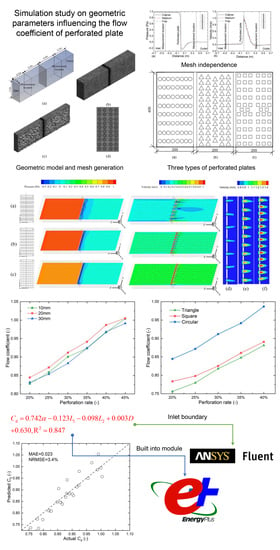
Simulation Study on Geometric Parameters Influencing the Flow Coefficient of Perforated Plate
Abstract
:1. Introduction
2. Methods
2.1. CFD Validation
2.2. Physical Models
2.2.1. Geometric Model and Boundary Conditions
2.2.2. Numerical Scenarios
2.2.3. Mesh Independence
2.3. CFD Governing Equations
2.4. Determination of the Flow Coefficient
3. Results
3.1. Impact of Perforation Rate on Flow Coefficient
3.2. Impact of Perforation Shape on Flow Coefficient
3.3. Impact of Perforation Size on Flow Coefficient
3.4. Correlation between Flow Coefficient and Geometric Parameters of Perforated Plate
4. Discussion
4.1. Application Analysis
4.2. Drawbacks and Future Works
5. Conclusions
- (1)
- The flow coefficient of a perforated plate is not a constant, which increases with the increase in the perforation rate and is slightly greater than that of ordinary building openings.
- (2)
- Under the same conditions, the corresponding flow coefficients of different holes rank as circle > square > triangle, and the circular hole can achieve higher flow coefficients and improve the effectiveness of natural ventilation.
- (3)
- Given the assumption of constant perforation shape, the flow coefficient increases with the increase in the perforation size, and this effect is greater when the size is small. The flow coefficient is less affected by the size of round holes compared to triangular and square holes.
- (4)
- The correlation between the flow coefficient and the geometric parameters of the perforated plate can be regressed by multiple linear functions, with the high precision of the adjusted R2 being 0.847. Both the perforation rate and the perforation size have a considerable positive influence on the flow coefficient, while the square and triangle holes have a negative influence on the flow coefficient compared with the circular hole. Moreover, the geometric parameters of perforated plates that have the greatest influence on flow coefficient are perforation rate, perforation shape, and size, in descending order.
- (5)
- The regression model can be used to select the type of perforated plate quickly and calculate its flow coefficient in a practical engineering project. By defining the pressure loss coefficient at the boundary, the model can also help simplify the geometric model in the simulation of building ventilation.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Cruz, H.; Viegas, J.C. On-site assessment of the discharge coefficient of open windows. Energy Build. 2016, 126, 463–476. [Google Scholar] [CrossRef]
- Zhou, J.; Hu, Y.; Zhang, G. Unsteady characteristics of natural wind and its influence on indoor environment. Sci. Technol. Rev. 2012, 30, 62–68. [Google Scholar]
- Yu, W.; Zhang, Y.; Du, C.; Li, B.; Liu, H.; Zhang, Y.; Wei, S. An innovative fan control strategy aimed at responding to human physiological characteristics for comfort sleeping. Therm. Sci. Eng. Prog. 2022, 35, 101470. [Google Scholar] [CrossRef]
- Tan, K.; Qin, Y.; Wang, J. Evaluation of the properties and carbon sequestration potential of biochar-modified pervious concrete. Constr. Build. Mater. 2022, 314, 125648. [Google Scholar] [CrossRef]
- Wang, J.; Meng, Q.; Yang, C.; Ren, P.; Santamouris, M. Spray optimization to enhance the cooling performance of transparent roofs in hot-humid areas. Energy Build. 2023, 286, 112929. [Google Scholar] [CrossRef]
- Schulze, T.; Eicker, U. Controlled natural ventilation for energy efficient buildings. Energy Build. 2013, 56, 221–232. [Google Scholar] [CrossRef]
- Bamdad, K.; Matour, S.; Izadyar, N.; Omrani, S. Impact of climate change on energy saving potentials of natural ventilation and ceiling fans in mixed-mode buildings. Build. Environ. 2022, 209, 108662. [Google Scholar] [CrossRef]
- He, B.-J.; Zhao, D.; Dong, X.; Xiong, K.; Feng, C.; Qi, Q.; Darko, A.; Sharifi, A.; Pathak, M. Perception, physiological and psychological impacts, adaptive awareness and knowledge, and climate justice under urban heat: A study in extremely hot-humid Chongqing, China. Sustain. Cities Soc. 2022, 79, 103685. [Google Scholar] [CrossRef]
- He, B.-J.; Zhao, D.; Dong, X.; Zhao, Z.; Li, L.; Duo, L.; Li, J. Will individuals visit hospitals when suffering heat-related illnesses? Yes, but…. Build. Environ. 2022, 208, 108587. [Google Scholar] [CrossRef]
- Gil-Baez, M.; Barrios-Padura, A.; Molina-Huelva, M.; Chacartegui, R. Natural ventilation systems in 21st-century for near zero energy school buildings. Energy 2017, 137, 1186–1200. [Google Scholar] [CrossRef]
- Ding, Y.; Li, B.; Shen, Y.; Su, Y. Numerical simulation of the effect of building layout and orientation on indoor natural ventilation. Civ. Archit. Environ. Eng. 2010, 32, 90–95. [Google Scholar]
- Cardinale, N.; Micucci, M.; Ruggiero, F. Analysis of energy saving using natural ventilation in a traditional Italian building. Energy Build. 2003, 35, 153–159. [Google Scholar] [CrossRef]
- Iqbal, A.; Afshari, A.; Wigo, H.; Heiselberg, P. Discharge coefficient of centre-pivot roof windows. Build. Environ. 2015, 92, 635–643. [Google Scholar] [CrossRef]
- ASHRAE. Handbook of Fundamentals; American Society of Heating, Refrigerating and Air Conditioning Engineers (ASHRAE): Peachtree Corners, GA, USA, 2001. [Google Scholar]
- Hunt, G.R.; Linden, P.P. The fluid mechanics of natural ventilation—Displacement ventilation by buoyancy-driven flows assisted by wind. Build. Environ. 1999, 34, 707–720. [Google Scholar] [CrossRef]
- Li, Y.G.; Delsante, A.; Chen, Z.D.; Sandberg, M.; Andersen, A.; Bjerre, M.; Heiselberg, P. Some examples of solution multiplicity in natural ventilation. Build. Environ. 2001, 36, 851–858. [Google Scholar] [CrossRef]
- Yi, Q.; Wang, X.; Zhang, G.; Li, H.; Janke, D.; Amon, T. Assessing effects of wind speed and wind direction on discharge coefficient of sidewall opening in a dairy building model—A numerical study. Comput. Electron. Agric. 2019, 162, 235–245. [Google Scholar] [CrossRef]
- Liao, Q.; Guan, Y.; Wang, Q. Research of window's discharge coefficient in the natural ventilation room. In Development of Industrial Manufacturing; Trans Tech Publications Ltd.: Baech, Switzerland, 2014; pp. 420–426. [Google Scholar]
- Wang, Y.; Yao, H.; Wen, F.; Chen, J. Analysis of the Building opening rate impact natural ventilation flow coefficient. Ind. Build. 2008, z1, 67–69. [Google Scholar]
- Chi, D.A.; Moreno, D.; Navarro, J. Impact of perforated solar screens on daylight availability and low energy use in offices. Adv. Build. Energy Res. 2021, 15, 117–141. [Google Scholar] [CrossRef]
- Chi, D.A.; Moreno, D.; Navarro, J. Statistical methods applied to optimize perforated facade design for daylight availability. J. Archit. Eng. 2019, 25, 04018034. [Google Scholar] [CrossRef]
- Blanco, J.M.; Arriaga, P.; Roji, E.; Cuadrado, J. Investigating the thermal behavior of double-skin perforated sheet facades: Part A: Model characterization and validation procedure. Build. Environ. 2014, 82, 50–62. [Google Scholar] [CrossRef]
- Zapico, A.; Egiluz, Z.; Frometa, Y.G.; Cuadrado, J. Mechanical characterization of double-skin perforated-sheet facades. J. Build. Eng. 2022, 56, 104750. [Google Scholar] [CrossRef]
- Miguel, A.F. Characterization of fluid flow through perforated plates. J. Porous Media 2019, 22, 1439–1448. [Google Scholar] [CrossRef]
- Basaran, T.; Inan, T. Experimental investigation of the pressure loss through a double skin facade by using perforated plates. Energy Build. 2016, 133, 628–639. [Google Scholar] [CrossRef] [Green Version]
- Tanner, P.; Gorman, J.; Sparrow, E. Flow-pressure drop characteristics of perforated plates. Int. J. Numer. Methods Heat Fluid Flow 2019, 29, 4310–4333. [Google Scholar] [CrossRef]
- Li, Y. Study on Ventilation Additional Resistance Characteristics of Perforated Plates. Master’s Thesis, Southwest Jiaotong University, Chengdu, China, 2016. [Google Scholar]
- Montazeri, H.; Montazeri, F. CFD simulation of cross-ventilation in buildings using rooftop wind-catchers: Impact of outlet openings. Renew. Energy 2018, 118, 502–520. [Google Scholar] [CrossRef]
- Bazdidi-Tehrani, F.; Masoumi-Verki, S.; Gholamalipour, P. Impact of opening shape on airflow and pollutant dispersion in a wind-driven cross-ventilated model building: Large eddy simulation. Sustain. Cities Soc. 2020, 61, 102196. [Google Scholar] [CrossRef]
- Shen, X.; Zhang, G.; Bjerg, B. Comparison of different methods for estimating ventilation rates through wind driven ventilated buildings. Energy Build. 2012, 54, 297–306. [Google Scholar] [CrossRef]
- Evola, G.; Popov, V. Computational analysis of wind driven natural ventilation in buildings. Energy Build. 2006, 38, 491–501. [Google Scholar] [CrossRef]
- Ramponi, R.; Blocken, B. CFD simulation of cross-ventilation for a generic isolated building: Impact of computational parameters. Build. Environ. 2012, 53, 34–48. [Google Scholar] [CrossRef]
- Huang, S.F.; Ma, T.Y.; Wang, D.; Lin, Z.H. Study on discharge coefficient of perforated orifices as a new kind of flowmeter. Exp. Therm. Fluid Sci. 2011, 25, 2237–2246. [Google Scholar] [CrossRef]
- Jin, T.; Tian, H.; Gao, X.; Liu, Y.; Wang, J.; Chen, H.; Lan, Y. Simulation and performance analysis of the perforated plate flowmeter for liquid hydrogen. Int. J. Hydrogen Energy 2017, 42, 3890–3898. [Google Scholar] [CrossRef]
- Zhou, X.-M.; Wang, Z.-K.; Zhang, Y.-F. A simple method for high-precision evaluation of valve flow coefficient by computational fluid dynamics simulation. Adv. Mech. Eng. 2017, 9, 1687814017713702. [Google Scholar] [CrossRef]
- Chen, C.; Zhou, H. Analysis of applied discharge coefficients of different types of ventilation devices based on CFD. J. HVAC 2018, 48, 87–91. [Google Scholar]
- Li, F. Adaptive Design of Perforated Metal Skin in Hot-Humid Area. Master’s Thesis, South China University of Technology, Guangzhou, China, 2012. [Google Scholar]
- Gong, G.; Li, H.; Nie, M.; Xie, G.; Li, Y. Discussion on the resistance property of natural ventilation induced by wind force. J. Hunan Univ. 2004, 31, 84–88. [Google Scholar]
- Heiselberg, P.; Svidt, K.; Nielsen, P.V. Characteristics of airflow from open windows. Build. Environ. 2001, 36, 859–869. [Google Scholar] [CrossRef]
- Andersen, K.T. Inlet and Outlet Coefficients—A Theoretical Analysis. In Proceedings of the 5th International Conference on Air Distribution in Rooms ROOMVENT’96, Tokyo, Japan, 17–19 July 1996; Volume 1. [Google Scholar]
- Srisamranrungruang, T.; Hiyama, K. Balancing of natural ventilation, daylight, thermal effect for a building with double-skin perforated facade (DSPF). Energy Build. 2020, 210, 109765. [Google Scholar] [CrossRef]
- Bingol, D.; Xiyili, H.; Elevli, S.; Kilic, E.; Cetintas, S. Comparison of multiple regression analysis using dummy variables and a NARX network model: An example of a heavy metal adsorption process. Water Environ. J. 2018, 32, 186–196. [Google Scholar] [CrossRef]
- Yi, Q.; Zhang, G.; Li, H.; Wang, X.; Janke, D.; Amon, B.; Hempel, S.; Amon, T. Estimation of opening discharge coefficient of naturally ventilated dairy buildings by response surface methodology. Comput. Electron. Agric. 2020, 169, 105224. [Google Scholar] [CrossRef]
- Chi, D.A.; Moreno, D.; Navarro, J. Design optimisation of perforated solar facades in order to balance daylighting with thermal performance. Build. Environ. 2017, 125, 383–400. [Google Scholar] [CrossRef]











| Group | Perforation Size (mm) | Perforation Rate (%) | Perforation Shape |
|---|---|---|---|
| A | 10, 20, 30 | 20, 25, 30, 35, 40, 45 | Circle |
| B | 20 | 20, 25, 30, 35, 40 | Circle |
| 27 | Triangle | ||
| 18 | Square | ||
| C | 10, 20, 30 | 20 | Circle |
| Triangle | |||
| Square |
| Perforation Shape | L1 | L2 |
|---|---|---|
| Circle | 0 | 0 |
| Square | 0 | 1 |
| Triangle | 1 | 0 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Peng, Y.; Mao, H.; Liu, Z.; Wei, C. Simulation Study on Geometric Parameters Influencing the Flow Coefficient of Perforated Plate. Buildings 2023, 13, 804. https://doi.org/10.3390/buildings13030804
Peng Y, Mao H, Liu Z, Wei C. Simulation Study on Geometric Parameters Influencing the Flow Coefficient of Perforated Plate. Buildings. 2023; 13(3):804. https://doi.org/10.3390/buildings13030804
Chicago/Turabian StylePeng, Yaogen, Huijun Mao, Zhichao Liu, and Cheng Wei. 2023. "Simulation Study on Geometric Parameters Influencing the Flow Coefficient of Perforated Plate" Buildings 13, no. 3: 804. https://doi.org/10.3390/buildings13030804
APA StylePeng, Y., Mao, H., Liu, Z., & Wei, C. (2023). Simulation Study on Geometric Parameters Influencing the Flow Coefficient of Perforated Plate. Buildings, 13(3), 804. https://doi.org/10.3390/buildings13030804