Analysis of the Northern Hemisphere Atmospheric Circulation Response to Arctic Ice Reduction Based on Simulation Results
Abstract
:1. Introduction
2. Methods
2.1. Local Wave Activity
2.2. Blocking Event Index
3. Model and Experiments
4. Results
4.1. Reduction of the Ice Volume and Its Area
4.2. Anomalies of Zonal Temperature Distribution and Zonal Wind
4.3. Wave Activity and Blockings
5. Discussion
- Increase in tropospheric temperature at latitude 60–70° N, and a decrease in stratospheric temperature at latitude 40–50° N, both cause a reduction in the gradient at the tropopause level in mid-latitudes. An increase in the temperature of the upper troposphere at latitude 20–30° N, and consequent increase in the gradient at the tropopause level at latitudes 30–40° N (Figure 4).
- Acceleration of the zonal flow at latitude 30–50° N, decelerating the flow at latitude 20–30° N. It means a shift of the jet to the north. Acceleration of eastern transport at latitude 80° N (Figure 5).
- Intensification of wave activity in Europe, Western America, and Chukotka, and its weakening in the south of Siberia and Kazakhstan (Figure 8).
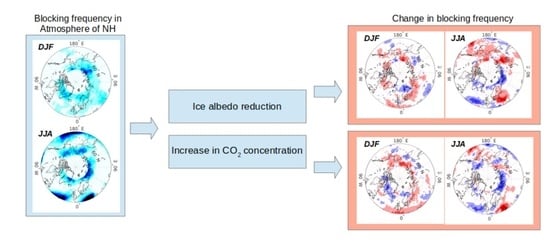
- Winter increase in the number of blockings in the East Siberian and Chukchi Seas, including Alaska, in central and eastern Europe and the reduction in blockings in the Norwegian Sea, Caspian region and Kazakhstan, and Yakutia (Figure 11).
- Summer decrease in the number of blockings on the line of the Barents-Kara-Laptev seas, in the Greenland region, in the central Atlantic and Pacific Oceans, but increase in the Yakutia, in northeastern Europe and the northeastern part of the Pacific Ocean (Figure 12).
- With minor changes in albedo, an increase in the polar stratospheric temperature (>1 °C), and with a significant increase in CO2 concentration, its decrease (1 °C);
- The temperature rise at the border of the troposphere and stratosphere in the tropics takes place only with an increase in the concentration of CO2.
- The deceleration of the flow at latitude 50–65° N occurs only with a decrease in albedo and disappears with an increase in CO2.
- Weakening of wave activity in the central part of the oceans in . Weakening in the northwestern part of the oceans in , while in , there is an increase.
- Winter increase in the number of blockings occurs in CAA in experiments , , and , while in experiment number of blockings decreases.
- Summer increase in the number of blockings occurs in the entire Bering Sea in and , while in the there is a slight decrease in the blocking frequency, and in the there is no significant trend.
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Andersen, J.K.; Andreassen, L.M.; Baker, E.H.; Ballinger, T.J.; Berner, L.T.; Bernhard, G.H.; Bhatt, U.S.; Bjerke, J.W.; Box, J.E.; Britt, L.; et al. The Arctic. Bull. Am. Meteorol. Soc. 2020, 101, S239–S286. [Google Scholar] [CrossRef]
- Wills, R.C.J.; White, R.H.; Levine, X.J. Northern Hemisphere Stationary Waves in a Changing Climate. Curr. Clim. Chang. Rep. 2019, 5, 372–389. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wu, B.; Handorf, D.; Dethloff, K.; Rinke, A.; Hu, A. Winter Weather Patterns over Northern Eurasia and Arctic Sea Ice Loss. Mon. Weather Rev. 2013, 141, 3786–3800. [Google Scholar] [CrossRef] [Green Version]
- McIntyre, M.E.; Palmer, T.N. Breaking planetary waves in the stratosphere. Nature 1983, 305, 593–600. [Google Scholar] [CrossRef]
- Polvani, L.M.; Saravanan, R. The Three-Dimensional Structure of Breaking Rossby Waves in the Polar Wintertime Stratosphere. J. Atmos. Sci. 2000, 57, 3663–3685. [Google Scholar] [CrossRef]
- Kim, B.M.; Son, S.W.; Min, S.K.; Jeong, J.H.; Kim, S.J.; Zhang, X.; Shim, T.; Yoon, J.H. Weakening of the stratospheric polar vortex by Arctic sea-ice loss. Nat. Commun. 2014, 5, 4646. [Google Scholar] [CrossRef] [Green Version]
- Sun, L.; Deser, C.; Tomas, R.A. Mechanisms of stratospheric and tropospheric circulation response to projected Arctic sea ice loss. J. Clim. 2015, 28, 7824–7845. [Google Scholar] [CrossRef]
- Strong, C.; Magnusdottir, G.; Stern, H. Observed feedback between winter sea ice and the North Atlantic Oscillation. J. Clim. 2009, 22, 6021–6032. [Google Scholar] [CrossRef]
- Deser, C.; Tomas, R.; Alexander, M.; Lawrence, D. The seasonal atmospheric response to projected Arctic sea ice loss in the late twenty-first century. J. Clim. 2010, 23, 333–351. [Google Scholar] [CrossRef] [Green Version]
- Sévellec, F.; Fedorov, A.; Liu, W. Arctic sea-ice decline weakens the Atlantic Meridional Overturning Circulation. Nat. Clim. Chang. 2017, 7, 604–610. [Google Scholar] [CrossRef]
- Drijfhout, S. Competition between global warming and an abrupt collapse of the AMOC in Earth’s energy imbalance. Sci. Rep. 2015, 5, 14877. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zhang, R.; Sutton, R.; Danabasoglu, G.; Kwon, Y.-O.; Marsh, R.; Yeager, S.G.; Amrhein, D.E.; Little, C.M. A review of the role of the Atlantic Meridional Overturning Circulation in Atlantic Multidecadal Variability and associated climate impacts. Rev. Geophys. 2019, 57, 316–375. [Google Scholar] [CrossRef] [Green Version]
- Posselt, D.J.; Heever, S.V.D.; Stephens, G.; Igel, M.R. Changes in the Interaction between Tropical Convection, Radiation, and the Large-Scale Circulation in a Warming Environment. J. Clim. 2012, 25, 557–571. [Google Scholar] [CrossRef] [Green Version]
- Cohen, J.; Zhang, X.; Francis, J.; Jung, T.; Kwok, R.; Overland, J.; Ballinger, T.J.; Bhatt, U.S.; Chen, H.W.; Coumou, D.; et al. Divergent consensuses on Arctic amplification influence on midlatitude severe winter weather. Nat. Clim. Chang. 2020, 10, 20–29. [Google Scholar] [CrossRef]
- Labe, Z.; Peings, Y.; Magnusdottir, G. Warm Arctic, cold Siberia pattern: Role of full Arctic amplification versus sea ice loss alone. Geophys. Res. Lett. 2020, 47, e2020GL088583. [Google Scholar] [CrossRef]
- Maykut, G.A.; Untersteiner, N. Some results from a time dependent, thermodynamic model of sea ice. J. Geophys. Res. 1971, 76, 1550–1575. [Google Scholar] [CrossRef]
- Curry, J.A.; Schramm, J.L.; Ebert, E.E. Sea ice-albedo climate feedback mechanism. J. Clim. 1995, 8, 240–247. [Google Scholar] [CrossRef]
- Sun, L.; Deser, C.; Tomas, R.A.; Alexander, M. Global coupled climate response to polar sea ice loss: Evaluating the effectiveness of different ice-constraining approaches. Geophys. Res. Lett. 2020, 47, e2019GL085788. [Google Scholar] [CrossRef]
- Chripko, S.; Msadek, R.; Sanchez-Gomez, E.; Terray, L.; Bessières, L.; Moine, M. Impact of Reduced Arctic Sea Ice on Northern Hemisphere Climate and Weather in Autumn and Winter. J. Clim. 2021, 34, 5847–5867. [Google Scholar] [CrossRef]
- Huang, C.S.Y.; Nakamura, N. Local Finite-Amplitude Wave Activity as a Diagnostic of Anomalous Weather Events. J. Atmos. Sci. 2016, 73, 211–229. [Google Scholar] [CrossRef]
- Rex, D. Blocking action in the middle troposphere and its effect upon regional climate: I. An aerological study of blocking action. Tellus 1950, 2, 196–211. [Google Scholar] [CrossRef] [Green Version]
- Green, J. The weather during July 1976: Some dynamical considerations of the drought. Weather 1977, 32, 120–126. [Google Scholar] [CrossRef]
- Hoskins, B.J.; James, I.N. Fluid Dynamics of the Mid-Latitude Atmosphere; John Wiley & Sons, Ltd.: Chichester, UK, 2014; pp. 337–360. [Google Scholar] [CrossRef]
- Woollings, T.; Barriopedro, D.; Methven, J.; Son, S.-W.; Martius, O.; Harvey, B.; Sillmann, J.; Lupo, A.R.; Seneviratne, S. Blocking and its response to climate change. Curr. Clim. Chang. Rep. 2018, 4, 287–300. [Google Scholar] [CrossRef] [Green Version]
- Chan, P.-W.; Hassanzadeh, P.; Kuang, Z. Evaluating indices of blocking anticyclones in terms of their linear relations with surface hot extremes. Geophys. Res. Lett. 2019, 46, 4904–4912. [Google Scholar] [CrossRef]
- Colucci, S.J. Planetary-scale preconditioning for the onset of blocking. J. Atmos. Sci. 2001, 58, 933–942. [Google Scholar] [CrossRef]
- Pelly, J.L.; Hoskins, B.J. How well does the ECMWF ensemble prediction system predict blocking? Q. J. R. Meteorol. Soc. 2003, 129, 1683–1702. [Google Scholar] [CrossRef]
- Jia, X.; Yang, S.; Song, W.; He, B. Prediction of wintertime Northern Hemisphere blocking by the NCEP Climate Forecast System. J. Meteorol. Res. 2014, 28, 76–90. [Google Scholar] [CrossRef]
- Shutts, G. The propagation of eddies in different jetstreams: Eddy vorticity forcing of ‘blocking’ flow fields. Q. J. R. Meteorol. Soc. 1983, 109, 737–761. [Google Scholar] [CrossRef]
- Trenberth, K. An assessment of the impact of transient eddies on the zonal flow during a blocking episode using localized Eliassen—Palm flux diagnostics. J. Atmos. Sci. 1986, 43, 2070–2087. [Google Scholar] [CrossRef] [Green Version]
- Mullen, S. Transient eddy forcing of blocking flows. J. Atmos. Sci. 1987, 44, 3–22. [Google Scholar] [CrossRef]
- Swanson, K. Stationary wave accumulation and the generation of low-frequency variability on zonally varying flows. J. Atmos. Sci. 2000, 57, 2262–2280. [Google Scholar] [CrossRef]
- Luo, D. A barotropic envelope Rossby soliton model for block-eddy interaction. Part I: Effect of topography. J. Atmos. Sci. 2005, 62, 5–21. [Google Scholar] [CrossRef]
- Barnes, E.A.; Slingo, J.; Woollings, T. A methodology for the comparison of blocking climatologies across indices, models and climate scenarios. Clim. Dyn. 2012, 38, 2467–2481. [Google Scholar] [CrossRef]
- Barnes, E.A.; Dunn-Sigouin, E.; Masato, G.; Woollings, T. Exploring recent trends in Northern Hemisphere blocking. Geophys. Res. Lett. 2014, 41, 638–644. [Google Scholar] [CrossRef]
- Andrews, D.G. A finite-amplitude Eliassen—Palm theorem in isentropic coordinates. J. Atmos. Sci. 1983, 40, 1877–1883. [Google Scholar] [CrossRef] [Green Version]
- Nakamura, N.; Solomon, A. Finite-Amplitude Wave Activity and Mean Flow Adjustments in the Atmospheric General Circulation. Part I: Quasigeostrophic Theory and Analysis. J. Atmos. Sci. 2010, 67, 3967–3983. [Google Scholar] [CrossRef]
- Nakamura, N.; Zhu, D. Finite-amplitude wave activity and diffusive flux of potential vorticity in eddy-mean flow interaction. J. Atmos. Sci. 2010, 67, 2701–2716. [Google Scholar] [CrossRef]
- Lubis, S.W.; Huang, C.S.Y.; Nakamura, N.; Omrani, N.; Jucker, M. Role of Finite-Amplitude Rossby Waves and Nonconservative Processes in Downward Migration of Extratropical Flow Anomalies. J. Atmos. Sci. 2018, 75, 1385–1401. [Google Scholar] [CrossRef]
- Norton, W.A. Breaking Rossby waves in a model stratosphere diagnosed by a vortex-following coordinate system and a technique for advecting material contours. J. Atmos. Sci. 1994, 51, 654–673. [Google Scholar] [CrossRef]
- Huang, C.S.Y.; Nakamura, N. Local wave activity budgets of the wintertime Northern Hemisphere: Implication for the Pacific and Atlantic storm tracks. Geophys. Res. Lett. 2017, 44, 5673–5682. [Google Scholar] [CrossRef]
- Chen, G.; Lu, J.; Burrows, D.A.; Leung, L.R. Local finite-amplitude wave activity as an objective diagnostic of midlatitude extreme weather. Geophys. Res. Lett. 2015, 42, 10952–10960. [Google Scholar] [CrossRef] [Green Version]
- Xue, D.; Lu, J.; Sun, L.; Chen, G.; Zhang, Y. Local increase of anticyclonic wave activity over northern Eurasia under amplified Arctic warming. Geophys. Res. Lett. 2017, 44, 3299–3308. [Google Scholar] [CrossRef]
- Tibaldi, S.; Molteni, F. On the Operational Predictability of Blocking. Tellus 1990, 42A, 343–365. [Google Scholar] [CrossRef] [Green Version]
- Scherrer, S.; Croci-Maspoli, M.; Schwierz, C.; Appenzeller, C. Two-dimensional indices of atmospheric blocking and their statistical relationship with winter climate patterns in the Euro-Atlantic region. Int. J. Climatol. 2006, 26, 233–249. [Google Scholar] [CrossRef]
- Davini, P. Atmospheric Blocking and Winter Mid-Latitude Climate Variability. Ph.D. Thesis, Università Ca’ Foscari, Venezia, Italy, 2013. [Google Scholar]
- D’Andrea, F.; Tibaldi, S.; Blackburn, M.; Boer, G.; Déqué, M.; Dix, M.R.; Dugas, B.; Ferranti, L.; Iwasaki, T.; Kitoh, A.; et al. Northern Hemisphere atmospheric blocking as simulated by 15 atmospheric general circulation models in the period 1979–1988. Clim. Dyn. 1998, 14, 385–407. [Google Scholar] [CrossRef]
- Volodin, E.M.; Mortikov, E.V.; Kostrykin, S.V.; Galin, V.Y.; Lykossov, V.N.; Gritsun, A.S.; Diansky, N.A.; Gusev, A.V.; Iakovlev, N.G.; Shestakova, A.A.; et al. Simulation of the modern climate using the INM-CM48 climate model. Russ. J. Numer. Anal. Math. Model. 2018, 33, 367–374. [Google Scholar] [CrossRef]
- Volodin, E.M.; Diansky, N.A.; Gusev, A.V. Simulation and Prediction of Climate Changes in the 19th to 21st Centuries with the Institute of Numerical Mathematics, Russian Academy of Sciences, Model of the Earth’s Climate System. Izvestiya. Atmos. Ocean. Phys. 2013, 49, 347–366. [Google Scholar] [CrossRef]
- Galin, V.Y. Parametrization of radiative processes in the DNM atmospheric model. Izvestiya. Atmos. Ocean. Phys. 1998, 34, 339–347. [Google Scholar]
- Dee, D.P.; Uppala, S.M.; Simmons, A.J.; Berrisford, P.; Poli, P.; Kobayashi, S.; Andrae, U.; Balmaseda, M.A.; Balsamo, G.; Bauer, D.P.; et al. The ERA-Interim reanalysis: Configuration and performance of the data assimilation system. Q. J. R. Meteorol. Soc. 2011, 137, 553–597. [Google Scholar] [CrossRef]
- Peings, Y.; Labe, Z.M.; Magnusdottir, G. Are 100 ensemble members enough to capture the remote atmospheric response to +2 °C Arctic sea ice loss? J. Clim. 2021, 34, 3751–3769. [Google Scholar] [CrossRef]
- Davini, P.; D’Andrea, F. From CMIP3 to CMIP6: Northern Hemisphere atmospheric blocking simulation in present and future climate. J. Clim. 2020, 33, 10021–10038. [Google Scholar] [CrossRef]
- Shaw, T.A. Mechanisms of Future Predicted Changes in the Zonal Mean Mid-Latitude Circulation. Curr. Clim. Chang. Rep. 2019, 5, 345–357. [Google Scholar] [CrossRef] [Green Version]
- Francis, J.A.; Vavrus, S.J. Evidence linking Arctic amplification to extreme weather in mid-latitudes. Geophys. Res. Lett. 2012, 39, L06801. [Google Scholar] [CrossRef]
- Screen, J.A.; Simmonds, I. Amplified mid-latitude planetary waves favour particular regional weather extremes. Nat. Clim. Chang. 2014, 4, 704–709. [Google Scholar] [CrossRef] [Green Version]
- Nakamura, N.; Huang, C.S.Y. Atmospheric blocking as a traffic jam in the jet stream. Science 2018, 361, 42–47. [Google Scholar] [CrossRef] [PubMed]
- Nakamura, H.; Lin, G.; Yamagata, T. Decadal climate variability in the North Pacific during the recent decades. Bull. Am. Meteorol. Soc. 1997, 78, 2215–2225. [Google Scholar] [CrossRef] [Green Version]
- Wiedenmann, J.; Lupo, A.; Mokhov, I.; Tikhonova, E. The Climatology of Blocking Anticyclones for the Northern and Southern Hemispheres: Block Intensity as a Diagnostic. J. Clim. 2002, 15, 3459–3473. [Google Scholar] [CrossRef] [Green Version]
- Screen, J.A.; Deser, C.; Smith, D.M.; Zhang, X.; Blackport, R.; Kushner, P.J.; Oudar, T.; McCusker, K.E.; Sun, L. Consistency and discrepancy in the atmospheric response to Arctic sea-ice loss across climate models. Nat. Geosci 2018, 11, 155–163. [Google Scholar] [CrossRef]
- Deser, C.; Phillips, A.S.; Bourdette, V.; Teng, H. Uncertainty in climate change projections: The role of internal variability. Clim. Dyn. 2012, 38, 527–546. [Google Scholar] [CrossRef] [Green Version]
- Yao, Y.; Luo, D.; Dai, A.; Simmonds, I. Increased quasi stationarity and persistence of winter Ural blocking and Eurasian extreme cold events in response to Arctic warming. Part I: Insights from observational analyses. J. Clim. 2017, 30, 3549–3568. [Google Scholar] [CrossRef]
- Hoskins, B.J.; Hodges, K.I. New perspectives on the Northern Hemisphere winter storm tracks. J. Atmos. Sci. 2002, 59, 1041–1061. [Google Scholar] [CrossRef]
- Held, I.M.; Ting, M.; Wang, H. Northern winter stationary waves: Theory and modeling. J. Clim. 2002, 15, 2125–2144. [Google Scholar] [CrossRef] [Green Version]
- Wilson, C.; Sinha, B.; Williams, R.G. The effect of ocean dynamics and orography on atmospheric storm tracks. J. Clim. 2009, 22, 3689–3702. [Google Scholar] [CrossRef] [Green Version]
- Nakamura, H. Midwinter suppression of baroclinic wave activity in the Pacific. J. Atmos. Sci. 1992, 49, 1629–1642. [Google Scholar] [CrossRef] [Green Version]
- Schiemann, R.; Athanasiadis, P.; Barriopedro, D.; Doblas-Reyes, F.; Lohmann, K.; Roberts, M.J.; Sein, D.V.; Roberts, C.D.; Terray, L.; Vidale, P.L. Northern Hemisphere blocking simulation in current climate models: Evaluating progress from the Climate Model Intercomparison Project Phase 5 to 6 and sensitivity to resolution. Weather Clim. Dyn. 2020, 1, 277–292. [Google Scholar] [CrossRef]



















| Initial Condition | Years 1–60 | Years 61–100 | |||
|---|---|---|---|---|---|
| Experiment | CO2, ppm | ||||
| 0.80 | 0.60 | 360 | |||
| : | 0.77 | 0.57 | 360 | ||
| Pre-industrial state | , | 0.70 | 0.50 | 360 | |
| CO2: 360 ppm | 0.80 | 0.60 | 450 | ||
| 0.80 | 0.60 | 600 | |||
| Experiment | (1), % | (2), % | (3), °C | (4), °C |
|---|---|---|---|---|
| 79 | 93 | 0.17 | 0.70 | |
| 25 | 66 | 0.30 | 1.7 | |
| 83 | 98 | 0.45 | 0.97 | |
| 77 | 90 | 1.0 | 1.8 |
| Experiment | Atlantic Ocean | Pacific Ocean | ||
|---|---|---|---|---|
| Coordinates | k, m·s 107 | Coordinates | k, m·s 107 | |
| 42 N, 28 W | −1.06 | 42 N, 148 W | −1.15 | |
| 40.5 N, 26 W | −1.21 | 39 N, 136 W | −1.28 | |
| 46.5 N, 4 W | −0.73 | 36 N, 178 W | −3.8 | |
| 45 N, 12 W | −0.99 | 37.5 N, 122 W | −0.94 | |
| 45 N, 18 W | −1.37 | 36 N, 162 W | −2.44 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Platov, G.; Krupchatnikov, V.; Gradov, V.; Borovko, I.; Volodin, E. Analysis of the Northern Hemisphere Atmospheric Circulation Response to Arctic Ice Reduction Based on Simulation Results. Geosciences 2021, 11, 373. https://doi.org/10.3390/geosciences11090373
Platov G, Krupchatnikov V, Gradov V, Borovko I, Volodin E. Analysis of the Northern Hemisphere Atmospheric Circulation Response to Arctic Ice Reduction Based on Simulation Results. Geosciences. 2021; 11(9):373. https://doi.org/10.3390/geosciences11090373
Chicago/Turabian StylePlatov, Gennady, Vladimir Krupchatnikov, Viacheslav Gradov, Irina Borovko, and Evgeny Volodin. 2021. "Analysis of the Northern Hemisphere Atmospheric Circulation Response to Arctic Ice Reduction Based on Simulation Results" Geosciences 11, no. 9: 373. https://doi.org/10.3390/geosciences11090373
APA StylePlatov, G., Krupchatnikov, V., Gradov, V., Borovko, I., & Volodin, E. (2021). Analysis of the Northern Hemisphere Atmospheric Circulation Response to Arctic Ice Reduction Based on Simulation Results. Geosciences, 11(9), 373. https://doi.org/10.3390/geosciences11090373