Seasonal Dynamics of Gaseous CO2 Concentrations in a Karst Cave Correspond with Aqueous Concentrations in a Stagnant Water Column
Abstract
:1. Introduction
2. Materials and Methods
2.1. The Site of the Measurement Campaign
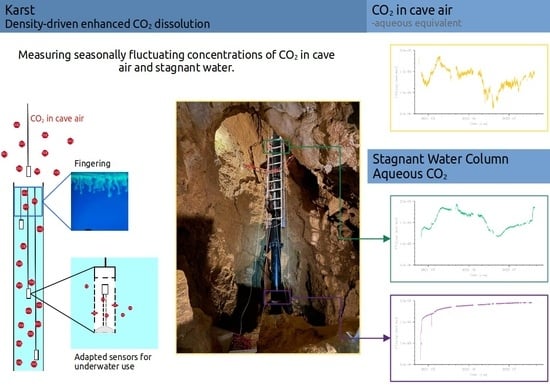
2.2. Monitoring CO2 Concentrations in Air and Water
2.3. Establishing Initial Conditions of the Measurements
2.4. The Numerical Model
2.4.1. Initial and Boundary Conditions of the Model
2.4.2. The Grid
3. Results
3.1. Data from Long-Term Monitoring
- The CO2 concentration in the cave’s atmosphere was, as expected, higher in summer than in winter. However, the late-summer peak values in 2021 and 2022 were notably different. Furthermore, a remarkable low was reached around March 2022, followed by a rise that started around April/May 2022.
- It is obvious that the sensor at the 5.85 m depth did not recognize the CO2 concentration dynamics in the cave air, whereas at the 1 m depth there was a clear trend indicating that the aqueous CO2 concentration followed the cave-air concentration.
- In June/July 2021, a strong increase in the cave-air concentration was followed by an increase of almost the same slope and peak value at the 1 m water depth. As the water is stagnant, the only process to drive this increase is convective mixing (i.e., density-driven enhanced dissolution). During the same time, the CO2 concentration at the 5.85 m depth increased, although with a smaller slope.
- Let us focus on the period between March and May/June 2022: there, we observe a strong low in the atmospheric CO2 concentration, which was followed with a small delay by the sensor at the 1 m depth, although the low is less pronounced. In a stagnant water column, we would expect only diffusion to be relevant for the release of CO2 from the water back to the atmosphere. However, as diffusion is an extremely slow process with characteristic time scales of several years related to distances of about 1 m, there has to be some small perturbation of the water in the shallower parts of the water column. We will discuss this later.
- The strong increase of the CO2 concentrations at the 1 m depth (green curve) in October 2022 can be explained by strong perturbances due to our activities during the control measurement campaign. It appears that a mixing was induced while removing the damaged sensor from the 5.85 m depth, which raised water of higher concentration from deeper regions. We decided to include these data in the plots, as they further strengthen confidence in the accuracy of our setup.
- The control measurement campaign with independent sensors and water samples demonstrated that the sensors used for long-term monitoring were in good agreement with the new sensors. In addition, CO2 concentrations obtained by direct sensor measurements agree with the CO2 concentrations calculated from TIC of water samples.
3.2. Comparison with Numerical Simulations
- The slope of the increase of CO2(aq) after an increase of CO2 in the cave air (e.g., the period from June 2021 to September 2021) is stronger in the measured data than predicted by the simulations. The ‘Super-Diffusion’ scenario is closest to match the slope.
- The shallower sensor at the 1 m depth shows sensitivity to periods of low cave-air concentrations (e.g., from May 2021 to June 2021 or from March 2022 to May 2022). This could not be reproduced by the simulations except for cases with artificially created perturbation as in the ‘Pulses’ scenario.
4. Discussion
4.1. Research Focus of the Study
4.2. Encountered Challenges
4.3. Comments on the Link between Cave Air CO2 and Precipitation Data
4.4. The (Dis-)Agreement between Data and Numerical Simulations
5. Conclusions
- Seasonal fluctuations of gaseous CO2 concentrations in cave air correspond with the concentrations of dissolved CO2 in stagnant water. With increasing depth, this correspondence diminishes. Although it was pronounced at a 1 m depth, there was, practically speaking, no effect anymore at a depth of 6 m.It can be concluded that deep water bodies under stagnant or close-to-stagnant conditions can act as efficient traps for CO2 after density-driven dissolution. It remains to be studied in future research how often such conditions are found in real karst settings to assess the relevance of this process for speleogenic theories in comparison to the classical processes relying on water flow.
- To the authors’ knowledge, this is the first time that the dynamics of CO2 at the gas–water interface and in different depths of a water body were monitored and modelled for real vadose conditions in a cave. It is therefore significant to note that the recognition of stagnant water bodies in caves to be efficient traps for CO2 stands on a solid basis.
- The data confirm quantitatively that under certain conditions (i.e., soil moisture, temperature, summer/winter), spikes in the concentrations of CO2 in the cave atmosphere coincide with periods of high precipitation. We observed a particularly strong high of CO2 in the cave air in late summer and early fall of 2021. We believe there is strong indication that this was the result of a relatively wet summer followed by an extremely dry period. Low soil moisture facilitates gas exchange between the cave and the soil and high soil-air CO2 concentrations can be transported into the karst system via gas-phase advection and dissolve at the water table.
- The comparison between the measured CO2 concentrations and numerical simulation results showed qualitative agreement, but the match is not satisfactory. The model predicted significantly smaller entry rates during periods of high air concentrations. In addition, the periods of low air concentrations, where the measurements show a decline also at the 1 m water depth, were (as expected!) not well matched by the model. Different reasons are discussed above and in Appendix C. Tiny perturbances are sufficient to improve the agreement for the declining CO2 concentration at the 1 m depth, although we were unable to determine their origin. A better match of the entry rates is expected for 3D simulations with high spatial and temporal resolution. Modellers with required capabilities are encouraged to use our datasets.
- Thin PVC-based membrane covers of CO2 sensors are well suited for short-term CO2 observations in water and guarantee a fast response time of the sensor. For time spans exceeding several months or years, material alterations and water vapour diffusion must be considered. To improve long-term stability and accuracy, silicon-based membrane covers might be an appropriate alternative.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| LW | Zweckverband Landeswasserversorgung—state water supply to the Laichingen region |
| DWD | Deutscher Wetterdienst—German Meteorological Service |
Appendix A. Measured Pressure and Temperature Data

Appendix B. Details on the Governing Model Equations
Appendix C. Investigations on Grid Convergence and 2D/3D Assumption
Appendix C.1. Grid Refinement Studies
| Case | Δ x [mm] | Δ y [mm] | Grading y | Δ t [s] |
|---|---|---|---|---|
| Baseline | 10 | 3 | −1.03 | 3600 |
| Baseline dx 5 | 5 | 3 | −1.03 | 3600 |
| Baseline dx 2.5 | 2.5 | 3 | −1.03 | 3600 |
| Baseline dx 1.25 | 1.25 | 3 | −1.03 | 3600 |
| Baseline dx 1.25 t 1800 | 1.25 | 3 | −1.03 | 1800 |
| Baseline dx 1 25 t 60 | 1.25 | 3 | −1.03 | 60 |
| Baseline dx 1.25 t 60 dy 1.5 | 1.25 | 1.5 | −1.03 | 60 |
| Baseline dx 1.25 t 3600 dy 1.5 | 1.25 | 1.5 | −1.03 | 3600 |
| Quadratic control t 3600 | 1.25 | 1.25 | 1 | 3600 |
| Quadratic control | 1.25 | 1.25 | 1 | 60 |




Appendix C.2. Comparison of 2D and 3D Domains


References
- Ford, D.; Williams, P. Karst Hydrogeology and Geomorphology; Wiley: Hoboken, NJ, USA, 2007. [Google Scholar] [CrossRef]
- Mangin, A. Contribution à l’étude Hydrodynamique Des Aquifères Karstiques. Ph.D. Thesis, Sciences de la Terre, Université de Dijon, Dijon, France, 1975. [Google Scholar]
- White, W. Caves and Karst of the Greenbrier Valley in West Virginia; Caves and Karst Systems of the World; Springer: Cham, Switzerland, 2018. [Google Scholar] [CrossRef]
- Dreybrodt, W. Processes in Karst Systems-Physics, Chemistry, and Geology; Physical Environment; Springer: Berlin/Heidelberg, Germany, 1988. [Google Scholar] [CrossRef]
- Bonacci, O. Karst Hydrology: With Special Reference to the Dinaric Karst; Physical Environment; Springer: Berlin/Heidelberg, Germany, 1987. [Google Scholar] [CrossRef]
- Stevanovic, Z. Karst Aquifers-Characterization and Engineering; Springer: Cham, Switzerland; Heidelberg, German; New York, NY, USA; Dordrecht, The Netherlands; London, UK, 2015. [Google Scholar] [CrossRef]
- Klimchouk, A.; Ford, D.; Palmer, A.; Dreybrodt, W. (Eds.) Speleogenesis-Evolution of Karst Aquifers; National Speleological Society: Huntsville, AL, USA, 2000.
- Bögli, A. Karst Hydrology and Physical Speleology; Springer: Berlin/Heidelberg, Germany, 1980. [Google Scholar] [CrossRef]
- Gabrovšek, F.; Dreybrodt, W. Role of mixing corrosion in calcite-aggressive H2O-CO2-CaCO3 solutions in the early evolution of karst aquifers in limestone. Water Resour. Res. 2000, 36, 1179–1188. [Google Scholar] [CrossRef]
- Ford, D.; Ewers, R. The development of limestone caves in the dimensions of length and depth. Int. J. Speleol. 1978, 10, 213–244. [Google Scholar] [CrossRef]
- Dreybrodt, W. Dissolution: Carbonate rocks. Encyclopedia of Caves and Karst Science; Taylor & Francis: London, UK, 2004; pp. 295–298. [Google Scholar]
- Kaufmann, G.; Gabrovšek, F.; Romanov, D. Deep conduit flow in karst aquifers revisited. Water Resour. Res. 2014, 50, 4821–4836. [Google Scholar] [CrossRef]
- Class, H.; Bürkle, P.; Sauerborn, T.; Trötschler, O.; Strauch, B.; Zimmer, M. On the role of density-driven dissolution of CO2 in phreatic karst systems. Water Resour. Res. 2021, 57, e2021WR030912. [Google Scholar] [CrossRef]
- IPCC. Special Report on Carbon Dioxide Capture and Storage. In Technical Report, Intergovernmental Panel on Climate Change (IPCC), prepared by Working Group III; Metz, B., Davidson, O., de Conink, H.C., Loos, M., Meyer, L.A., Eds.; Cambridge University Press: Cambridge, UK; New York, NY, USA, 2005. [Google Scholar]
- Green, C.; Ennis-King, J. Steady flux regime during convective mixing in three-dimensional heterogeneous porous media. Fluids 2018, 3, 58. [Google Scholar] [CrossRef]
- Covington, M. The importance of advection for CO2 dynamics in the karst critical zone: An approach from dimensional analysis. In Caves and Karst Across Time; Special Paper 516; Feinberg, J., Gao, Y., Alexander, E., Eds.; Geological Society of America: Boulder, CO, USA, 2016. [Google Scholar] [CrossRef]
- Ennis-King, J.; Paterson, L. Rate of dissolution due to convective mixing in the underground storage of carbon dioxide. In Greenhouse Gas Control Technologies; Gale, J., Kaya, Y., Eds.; Elsevier: Amsterdam, The Netherlands, 2003; Volume 1, pp. 507–510. [Google Scholar] [CrossRef]
- Ennis-King, J.; Paterson, L. Role of convective mixing in the long-term storage of carbon dioxide in deep saline formations. In Proceedings of the Annual Fall Technical Conference and Exhibition, Denver, CO, USA, 5–8 October 2003; Society of Petroleum Engineers: Richardson, TX, USA, 2003. Number SPE-84344. [Google Scholar] [CrossRef]
- Riaz, A.; Hesse, M.; Tchelepi, H.; Orr, F. Onset of convection in a gravitationally unstable diffusive boundary layer in porous media. J. Fluid Mech. 2006, 548, 87–111. [Google Scholar] [CrossRef]
- Hassanzadeh, H.; Pooladi-Darvish, M.; Keith, D. Modelling of convective mixing in CO2 storage. J. Can. Pet. Technol. 2005, 44. [Google Scholar] [CrossRef]
- Hassanzadeh, H.; Pooladi-Darvish, M.; Keith, D. Stability of a fluid in a horizontal saturated porous layer: Effect of non-linear concentration profile, initial, and boundary conditions. Transp. Porous Media 2006, 65, 193–211. [Google Scholar] [CrossRef]
- Emami-Meybodi, H.; Hassanzadeh, H.; Green, C.; Ennis-King, J. Convective dissolution of CO2 in saline aquifers: Progress in modeling and experiments. Int. J. Greenh. Gas Control. 2015, 40, 238–266. [Google Scholar] [CrossRef]
- Hassanzadeh, H.; Pooladi-Darvish, M.; Keith, D. Scaling behavior of convective mixing, with application to geological storage of CO2. Am. Inst. Chem. Eng. J. 2007, 53, 1121–1131. [Google Scholar] [CrossRef]
- Pau, G.; Bell, J.; Pruess, K.; Almgren, A.; Lijewski, M.; Zhang, K. High resolution simulation and characterization of density-driven flow in CO2 storage in saline aquifers. Adv. Water Resour. 2010, 33, 443–455. [Google Scholar] [CrossRef]
- Keim, L.; Class, H.; Schirmer, L.; Wendel, K.; Strauch, B.; Zimmer, M. Data for: Measurement Campaign of Gaseous CO2 Concentrations in a Karst Cave with Aqueous Concentrations in a Stagnant Water Column 2021–2022. Tech. Rep. 2022. [Google Scholar] [CrossRef]
- Frank, R. Zur Morphologie der Laichinger Tiefenhöhle. Laichinger Höhlenfreund. 2019, 54, 33–48. Available online: https://www.academia.edu/45140466 (accessed on 22 January 2023).
- Selg, M.; Schwarz, K. Am Puls der schönen Lau-zur Hydrogeologie des Blautopf-Einzugsgebiets. Laichinger Höhlenfreund. 2009, 44, 45–72. Available online: http://www.blauhoehle.org/images/pdf/hydrogeologie_blautopf.pdf (accessed on 22 January 2023).
- Kjeldsen, P. Evaluation of gas diffusion through plastic materials used in experimental and sampling equipment. Water Res. 1993, 27, 121–131. [Google Scholar] [CrossRef]
- Zimmer, M.; Erzinger, J.; Kujawa, C.; CO2-SINK-Group. The gas membrane sensor (GMS): A new method for gas measurements in deep boreholes applied at the CO2 SINK site. Int. J. Greenh. Gas Control 2011, 5, 995–1001. [Google Scholar] [CrossRef]
- De Gregorio, S.; Camarda, M.; Longo, M.; Cappuzzo, S.; Giudice, G.; Gurrieri, S. Long-term continuous monitoring of the dissolved CO2 performed by using a new device in groundwater of the Mt. Etna (southern Italy). Water Res. 2011, 45, 3005–3011. [Google Scholar] [CrossRef]
- Johnson, M.; Billett, M.; Dinsmore, K.; Wallin, M.; Dyson, K.; Jassal, R. Direct and continuous measurement of dissolved carbon dioxide in freshwater aquatic systems method and applications. Ecohydrology 2010, 3, 68–78. [Google Scholar] [CrossRef]
- Strauch, B.; Heeschen, K.U.; Schicks, J.M.; Spangenberg, E.; Zimmer, M. Application of tubular silicone (PDMS) membranes for gas monitoring in CO2–CH4 hydrate exchange experiments. Mar. Pet. Geol. 2020, 122, 104677. [Google Scholar] [CrossRef]
- Roy, R.N.; Roy, L.N.; Vogel, K.M.; Porter-Moore, C.; Pearson, T.; Good, C.E.; Millero, F.J.; Campbell, D.M. The dissociation constants of carbonic acid in seawater at salinities 5 to 45 and temperatures 0 to 45°C. Mar. Chem. 1993, 44, 249–267. [Google Scholar] [CrossRef]
- Millero, F.J. The thermodynamics of the carbonate system in seawater. Geochim. Cosmochim. Acta 1979, 43, 1651–1661. [Google Scholar] [CrossRef]
- Leal, A. Reaktoro: An Open-Source Unified Framework for Modeling Chemically Reactive Systems. 2015. Available online: https://reaktoro.org (accessed on 2 February 2023).
- Class, H.; Weishaupt, K.; Trötschler, O. Experimental and Simulation Study on Validating a Numerical Model for CO2 Density-Driven Dissolution in Water. Water 2020, 12, 738. [Google Scholar] [CrossRef]
- Koch, T.; Gläser, D.; Weishaupt, K.; Ackermann, S.; Beck, M.; Becker, B.; Burbulla, S.; Class, H.; Coltman, E.; Emmert, S.; et al. DuMux 3—An open-source simulator for solving flow and transport problems in porous media with a focus on model coupling. Comput. Math. Appl. 2021. [Google Scholar] [CrossRef]
- DuMux Handbook. Available online: https://dumux.org/docs/handbook/master/dumux-handbook.pdf (accessed on 2 February 2023).
- Peyraube, N.; Lastennet, R.; Denis, A.; Malaurent, P.; Villanueva, J. Interpreting CO2-SIc relationship to estimate CO2 baseline in limestone aquifers. Environ. Earth Sci. 2015, 1, 19–26. [Google Scholar] [CrossRef]
- Schimel, J. Life in dry soils: Effects of drought on soil microbial communities and processes. Annu. Rev. Ecol. Evol. Syst. 2018, 49, 409–432. [Google Scholar] [CrossRef]
- von Lützow, M.; Kögel-Knabner, I. Temperature sensitivity of soil organic matter decomposition—What do we know? Biol. Fertil. Soils 2009, 46, 1–15. [Google Scholar] [CrossRef]
- Keim, L.; Class, H.; Schirmer, L.; Strauch, B.; Wendel, K.; Zimmer, M. Code for: Seasonal Dynamics of Gaseous CO2 Concentrations in a Karst Cave Correspond with Aqueous Concentrations in a Stagnant Water Column. Tech. Rep. 2022. [Google Scholar] [CrossRef]
- Tsinober, A.; Rosenzweig, R.; Class, H.; Helmig, R.; Shavit, U. The role of mixed convection and hydrodynamic dispersion during CO2 dissolution in saline aquifers: A numerical study. Water Resour. Res. 2021, 58, e2021WR030494. [Google Scholar] [CrossRef]
- Ito, M.; Nagai, K. Analysis of degradation mechanism of plasticized PVC under artificial aging conditions. Polym. Degrad. Stab. 2007, 92, 260–270. [Google Scholar] [CrossRef]
- Ma, J.; Lio, R.; Tsang, L.S.; Lan, Z.D.; Li, Y. A downward CO2 flux seems to have nowhere to go. Biogeosciences 2014, 11, 6251–6262. [Google Scholar] [CrossRef] [Green Version]
- Garcia, J. Density of Aqueous Solutions of CO2; Technical Report, LBNL Report 49023; Lawrence Berkeley National Laboratory: Berkeley, CA, USA, 2001.








| Sample | Depth [m] | Temperature [°C] | pH [-] | Sk,4.3 [mmol/L] | Sk,8.2 [mmol/L] | CO2(aq) [mol/mol] |
|---|---|---|---|---|---|---|
| 10-24 | 5.85 | 8 | 6.8 | 8.7 | 5.2 | 2.06 × 10−5 |
| 8.4 | 5.0 | |||||
| 8.8 | 4.9 | |||||
| 11-04 | 1.0 | 8 | 6.84 | 8.5 | 4.4 | 1.92 × 10−5 |
| 7 | 3.6 | |||||
| 7.1 | 3.6 | |||||
| Tap water | 13.9 | 7.3 | 0.8 × 10−5 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Class, H.; Keim, L.; Schirmer, L.; Strauch, B.; Wendel, K.; Zimmer, M. Seasonal Dynamics of Gaseous CO2 Concentrations in a Karst Cave Correspond with Aqueous Concentrations in a Stagnant Water Column. Geosciences 2023, 13, 51. https://doi.org/10.3390/geosciences13020051
Class H, Keim L, Schirmer L, Strauch B, Wendel K, Zimmer M. Seasonal Dynamics of Gaseous CO2 Concentrations in a Karst Cave Correspond with Aqueous Concentrations in a Stagnant Water Column. Geosciences. 2023; 13(2):51. https://doi.org/10.3390/geosciences13020051
Chicago/Turabian StyleClass, Holger, Leon Keim, Larissa Schirmer, Bettina Strauch, Kai Wendel, and Martin Zimmer. 2023. "Seasonal Dynamics of Gaseous CO2 Concentrations in a Karst Cave Correspond with Aqueous Concentrations in a Stagnant Water Column" Geosciences 13, no. 2: 51. https://doi.org/10.3390/geosciences13020051
APA StyleClass, H., Keim, L., Schirmer, L., Strauch, B., Wendel, K., & Zimmer, M. (2023). Seasonal Dynamics of Gaseous CO2 Concentrations in a Karst Cave Correspond with Aqueous Concentrations in a Stagnant Water Column. Geosciences, 13(2), 51. https://doi.org/10.3390/geosciences13020051