Estimating Groundwater Abstractions at the Aquifer Scale Using GRACE Observations
Abstract
:1. Introduction
2. Materials and Methods
2.1. Study Area Description
2.2. Description of the Data Set
2.2.1. GRACE Data
2.2.2. Ground Observations
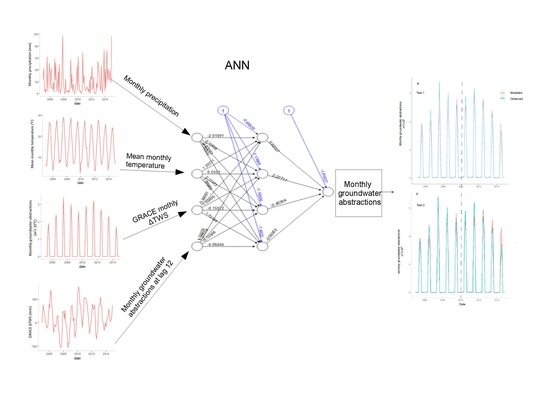
2.3. The ANN Model
- (a)
- Scaled Root Mean Square Error (RMSE) ranging from 0 to a large value, denoted as R*:
- (b)
3. Results and Discussion
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Conflicts of Interest
References
- Miro, M.E.; Famiglietti, J.S. Downscaling GRACE remote sensing datasets to high-resolution groundwater storage change maps of California’s Central Valley. Remote Sens. 2018, 10. [Google Scholar] [CrossRef]
- Taylor, C.; Alley, W. Ground-Water-Level Monitoring and the Importance of Long-Term Water-Level Data; USGS Circular 1217; US Geological Survey: Reston, VA, USA, 2001.
- Brunner, P.; Hendricks Franssen, H.-J.; Kgotlhang, L.; Bauer-Gottwein, P.; Kinzelbach, W. How can remote sensing contribute in groundwater modeling? Hydrogeol. J. 2007, 15, 5–18. [Google Scholar] [CrossRef]
- Wada, Y.; Van Beek, L.P.H.; Van Kempen, C.M.; Reckman, J.T.M.; Vasak, S.; Bierkens, M.P. Global depletion of groundwater resources. Geophys. Res. Lett. 2010, 37, 1–5. [Google Scholar] [CrossRef]
- Döll, P. Vulnerability to the impact of climate change on renewable groundwater resources: A global-scale assessment. Environ. Res. Lett. 2009, 4, 1–12. [Google Scholar] [CrossRef]
- Giorgi, F. Climate change hot-spots. Geophys. Res. Lett. 2006, 33, L08707. [Google Scholar] [CrossRef]
- Giorgi, F.; Lionello, P. Climate change projections for the Mediterranean region. Glob. Planet. Chang. 2008, 63, 90–104. [Google Scholar] [CrossRef]
- Neteler, M. Estimating daily land surface temperatures in mountainous environments by reconstructed MODIS LST data. Remote Sens. 2010, 2, 333–351. [Google Scholar] [CrossRef]
- Alsdorf, D.E.; Rodriguez, E.; Lettenmaier, D.P. Measuring surface water from space. Rev. Geophys. 2007, 45, 1–24. [Google Scholar] [CrossRef]
- Sun, A.Y. Predicting groundwater level changes using GRACE data. Water Resour. Res. 2013, 49, 5900–5912. [Google Scholar] [CrossRef] [Green Version]
- Lakshmi, V. Beyond GRACE: Using Satellite Data for Groundwater Investigations. Groundwater 2016, 54, 615–618. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Richey, A.S.; Thomas, B.F.; Lo, M.-H.; Reager, J.T.; Famiglietti, J.S.; Voss, K.; Swenson, S.; Rodell, M. Quantifying renewable groundwater stress with GRACE. Water Resour. Res. 2015, 51, 5217–5238. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Gemitzi, A.; Lakshmi, V. Evaluating Renewable Groundwater Stress with GRACE Data in Greece. Groundwater 2018, 56, 501–514. [Google Scholar] [CrossRef] [PubMed]
- Long, D.; Scanlon, B.R.; Longuevergne, L.; Sun, A.Y.; Fernando, D.N.; Save, H. GRACE satellite monitoring of large depletion in water storage in response to the 2011 drought in Texas. Geophys. Res. Lett. 2013, 40. [Google Scholar] [CrossRef] [Green Version]
- Gemitzi, A.; Petalas, C.; Pisinaras, V.; Tsihrintzis, V.A. Spatial prediction of nitrate pollution in groundwaters using neural networks and GIS: An application to South Rhodope aquifer (Thrace, Greece). Hydrol. Process. 2009, 23, 372–383. [Google Scholar] [CrossRef]
- Gemitzi, A.; Stefanopoulos, K.; Schmidt, M.; Richnow, H.H. Seawater intrusion into groundwater aquifer through a coastal lake—Complex interaction characterised by water isotopes 2H and 18O. Isotopes Environ. Health Stud. 2014, 50, 74–87. [Google Scholar] [CrossRef] [PubMed]
- Gemitzi, A.; Stefanopoulos, K. Evaluation of the effects of climate and man intervention on ground waters and their dependent ecosystems using time series analysis. J. Hydrol. 2011, 403, 130–140. [Google Scholar] [CrossRef]
- Gemitzi, A. Evaluating the anthropogenic impacts on groundwaters; a methodology based on the determination of natural background levels and threshold values. Environ. Earth Sci. 2012, 67, 2223–2237. [Google Scholar] [CrossRef]
- Swenson, S.C. GRACE monthly land water mass grids Netcdf Release 5.0; Ver. 5.0. Physical Oceanography Distributed Active Archive Center, CA, USA. 2012. Available online: https://podaac.jpl.nasa.gov/dataset/TELLUS_LAND_NC_RL05 (accessed on 8 August 2017).
- Landerer, F.W.; Swenson, S.C. Accuracy of scaled GRACE terrestrial water storage estimates. Water Resour. Res. 2012, 48, 1–11. [Google Scholar] [CrossRef]
- Wahr, J.; Molenaar, M.; Bryan, F. Time-variability of the Earth’s gravity field: Hydrological and oceanic effects and their possible detection using GRACE. J. Geophys. Res. 1998, 103, 30205–30230. [Google Scholar] [CrossRef]
- Tapley, B.D.; Bettadpur, S.; Ries, J.C.; Thompson, P.F.; Watkins, M.M. GRACE Measurements of Mass Variability in the Earth System. Science 2004, 305, 503–505. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Faour, K. Winter Crop Budgets, Southern Zone 2001; NSW Agriculture: Leeton Shire, Australia, 2001. [Google Scholar]
- Coulibaly, P.; Anctil, F.; Aravena, R.; Bobée, B. Artificial neural network modeling of water table depth fluctuations. Water Resour. Res. 2001, 37, 885–896. [Google Scholar] [CrossRef] [Green Version]
- Chu, H.-J.; Chang, L.-C. Optimal control algorithm and neural network for dynamic groundwater management. Hydrol. Process. 2009, 23, 2765–2773. [Google Scholar] [CrossRef]
- Coppola, E.A.; Szidarovszky, F.; Davis, D.; Spayd, S.; Poulton, M.M.; Roman, E. Multiobjective analysis of a public wellfield using artificial neural networks. Ground Water 2007, 45, 53–61. [Google Scholar] [CrossRef] [PubMed]
- Huang, Z.; Pan, Y.; Gong, H.; Yeh, P.J.; Li, X.; Zhou, D.; Zhao, W. Subregional-scale groundwater depletion detected by GRACE for both shallow and deep aquifers in North China Plain. Geophys. Res. Lett. 2015, 42, 1791–1799. [Google Scholar] [CrossRef] [Green Version]
- Scanlon, B.R.; Longuevergne, L.; Long, D. Ground referencing GRACE satellite estimates of groundwater storage changes in the California Central Valley, USA. Water Resour. Res. 2012, 48, 1–9. [Google Scholar] [CrossRef]
- Tachi, S.E.; Ouerdachi, L.; Remaoun, M.; Derdous, O.; Boutaghane, H. Forecasting suspended sediment load using regularized neural network: Case study of the Isser River (Algeria). J. Water Land Dev. 2016, 29, 75–81. [Google Scholar] [CrossRef] [Green Version]
- Zhou, Z.-H. Ensemble Methods: Foundations and Algorithms; Taylor & Francis Group, LLC: Abingdon, UK, 2012; ISBN 9781439830055. [Google Scholar]
- Dietterich, T.G. Ensemble Methods in Machine Learning. In Multiple Classifier Systems; Kittler, J., Roli, F., Eds.; Springer: Heidelberg, Germany, 2000; pp. 1–15. ISBN 978-3-540-67704-8. [Google Scholar]
- Fritsch, S.; Guenther, F.; Suling, M.; Mueller, S.M. Package ‘Neuralnet’; The Comprehensive R Archive Network: Hoboken, NJ, USA, 2016. [Google Scholar]
- Legates, D.R.; McCabe, G.J., Jr. Evaluating the Use of “Goodness of Fit” Measures in Hydrologic and Hydroclimatic Model Validation. Water Resour. Res. 2005, 35, 233–241. [Google Scholar] [CrossRef]
- Groenendijk, P.; Heinen, M.; Klammler, G.; Fank, J.; Kupfersberger, H.; Pisinaras, V.; Gemitzi, A.; Peña-Haro, S.; García-Prats, A.; Pulido-Velazquez, M.; et al. Performance assessment of nitrate leaching models for highly vulnerable soils used in low-input farming based on lysimeter data. Sci. Total Environ. 2014, 499, 463–480. [Google Scholar] [CrossRef] [PubMed]
- Nash, J.E.; Sutcliffe, J.V. River Flow Forecasting Through Conceptual Models Part I—A Discussion of Principles*. J. Hydrol. 1970, 10, 282–290. [Google Scholar] [CrossRef]
- Moriasi, D.N.; Arnold, J.G.; Van Liew, M.W.; Bingner, R.L.; Harmel, R.D.; Veith, T.L. Model Evaluation Guidelines for Systematic Quantification of Accuracy in Watershed Simulations. Trans. ASABE 2007, 50, 885–900. [Google Scholar] [CrossRef]
- Olden, J.D.; Joy, M.K.; Death, R.G. An accurate comparison of methods for quantifying variable importance in artificial neural networks using simulated data. Ecol. Model. 2004, 178, 389–397. [Google Scholar] [CrossRef]
- Wang, X.; De Linage, C.; Famiglietti, J.; Zender, C.S. Gravity Recovery and Climate Experiment (GRACE) detection of water storage changes in the Three Gorges Reservoir of China and comparison with in-situ measurements. Water Resour. Res. 2011, 47, 1–13. [Google Scholar] [CrossRef]






| Parameter | Minimum Value | Maximum Value | Standard Deviation |
|---|---|---|---|
| Monthly precipitation (mm) | 0.0 | 241.0 | 52.2 |
| Mean monthly temperature (°C) | 2.2 | 29.0 | 7.5 |
| GRACE Total Water Storage anomalies—ΔTWS (mm/month) | −107.3 | 152.7 | 57.2 |
| Monthly groundwater abstractions (m3 × 106) * | 1.2 | 3.4 | 0.58 |
| Parameter | Cross-Correlation Function | Time Lag (Months) |
|---|---|---|
| Monthly precipitation | −0.3 | 0 |
| Mean monthly temperature | 0.72 | 0 |
| GRACE Total Water Storage anomalies—ΔTWS | −0.33 | 0 |
| Monthly groundwater abstractions | 0.89 * | 12 |
| Input Variables | Architecture * | R* | NSE |
|---|---|---|---|
| Abstractions (Lag 12) | 3 3:1 | 0.35 | 0.77 |
| Mean monthly temperature GRACE monthly ΔΤWS | 3:4:1 | 0.31 | 0.79 |
| Abstractions (Lag 12) | 3 3:1 | 0.41 | 0.72 |
| GRACE monthly ΔTWS Monthly precipitation | 3:4:1 | 0.38 | 0.78 |
| Abstractions (Lag 12) | 3:3:1 | 0.44 | 0.65 |
| Mean monthly temperature Monthly precipitation | 3:4:1 | 0.41 | 0.69 |
| GRACE monthly ΔTWS | 3:3:1 | 0.91 | 0.43 |
| Mean monthly temperature Monthly precipitation | 3:4:1 | 0.88 | 0.45 |
| Abstractions (Lag 12) | 4:3:1 | 0.29 | 0.82 |
| Mean monthly temperature | 4:4:1 | 0.23 | 0.95 |
| Monthly precipitation | 4:5:1 | 0.31 | 0.80 |
| GRACE monthly ΔTWS | 4:6:1 | 0.35 | 0.78 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gemitzi, A.; Lakshmi, V. Estimating Groundwater Abstractions at the Aquifer Scale Using GRACE Observations. Geosciences 2018, 8, 419. https://doi.org/10.3390/geosciences8110419
Gemitzi A, Lakshmi V. Estimating Groundwater Abstractions at the Aquifer Scale Using GRACE Observations. Geosciences. 2018; 8(11):419. https://doi.org/10.3390/geosciences8110419
Chicago/Turabian StyleGemitzi, Alexandra, and Venkat Lakshmi. 2018. "Estimating Groundwater Abstractions at the Aquifer Scale Using GRACE Observations" Geosciences 8, no. 11: 419. https://doi.org/10.3390/geosciences8110419
APA StyleGemitzi, A., & Lakshmi, V. (2018). Estimating Groundwater Abstractions at the Aquifer Scale Using GRACE Observations. Geosciences, 8(11), 419. https://doi.org/10.3390/geosciences8110419