Multiblock Analysis Applied to TD-NMR of Butters and Related Products
Abstract
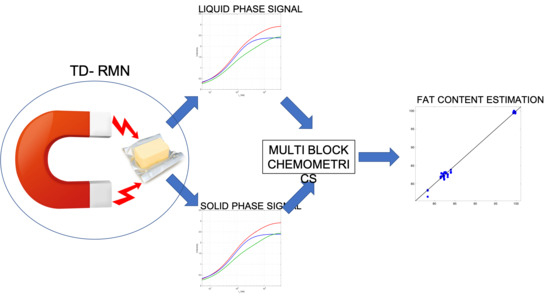
:1. Introduction
2. Material and Methods
2.1. Samples
2.2. Methods
2.3. Data Processing
2.3.1. PLS and SO-PLS
- The response is fitted to by PLS using K1 latent variables.
- is orthogonalized with respect to the K1 scores extracted from the first block.
- The -residual obtained from step 1 is fitted to by PLS using K2 latent variables.
- The scores produced at steps 1 and 3 are then used in an MLR to predict the response y.
2.3.2. CovSel and SO-CovSel
- Calculation of the squared covariance between the columns of X and y:
- Selection of the variable I corresponding to the maximum value of c:
- Projection of X and y orthogonally to the column I of X:
2.3.3. Figures of Merit
3. Results and Discussion
3.1. NMR Signal Description
3.2. Mono Block Calibrations
3.3. Multi Block Calibrations
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Duval, F.P.; van Duynhoven, J.P.; Bot, A. Practical implications of the phase-compositional assessment of lipid-based food products by time-domain NMR. J. Am. Oil Chem. Soc. 2006, 83, 905–912. [Google Scholar] [CrossRef]
- Mariette, F. Investigations of food colloids by NMR and MRI. Curr. Opin. Colloid Interface Sci. 2009, 14, 203–211. [Google Scholar] [CrossRef] [Green Version]
- Trezza, E.; Haiduc, A.M.; Goudappel, G.J.W.; Van Duynhoven, J.P.M. Rapid phase-compositional assessment of lipid-based food products by time domain NMR. Magn. Reson. Chem. 2006, 44, 1023–1030. [Google Scholar] [CrossRef] [PubMed]
- Mariette, F.; Lucas, T. NMR signal analysis to attribute the components to the solid/liquid phases present in mixes and ice creams. J. Agric. Food Chem. 2005, 53, 1317–1327. [Google Scholar] [CrossRef] [PubMed]
- Rutledge, D.N.; Barros, A.S.; Gaudard, F. ANOVA and Factor Analysis Applied to Time Domain NMR Signals. Magn. Reson. Chem. 1997, 35, S13–S21. [Google Scholar] [CrossRef]
- Rutledge, D.N.; Barros, A.S.; Vackier, M.C.; Baumberger, S.; Lapierre, C. Analysis of Time Domain NMR and Other Signals. In Advances in Magnetic Resonance in Food Science; Belton, P.S., Hills, B.P., Webb, G.A., Eds.; Royal Society of Chemistry Special Publications: Cambridge, UK, 1999; pp. 203–216. [Google Scholar]
- Wold, S.; Sjöström, M.; Eriksson, L. PLS-regression: A basic tool of chemometrics. Chemom. Intell. Lab. Syst. 2001, 58, 109–130. [Google Scholar] [CrossRef]
- Jepsen, S.M.; Pedersen, H.T.; Engelsen, S.B. Application of Chemometrics to Low-Field (1)H NMR Relaxation Data of Intact Fish Flesh. J. Sci. Food Agric. 1999, 79, 1793–1802. [Google Scholar] [CrossRef]
- Pedersen, H.T.; Bro, R.; Engelsen, S.B. Towards Rapid and Unique Curve Resolution of Low-Field NMR Relaxation Data: Trilinear Slicing Versus Two-Dimensional Curve Fitting. J. Magn. Reson. 2002, 157, 141–155. [Google Scholar] [CrossRef]
- Pedersen, H.T.; Munck, L.; Engelsen, S.B. Low-Field H-1 Nuclear Magnetic Resonance and Chemometrics Combined for Simultaneous Determination of Water, Oil, and Protein Contents in Oilseeds. J. Am. Oil Chem. Soc. 2000, 77, 1069–1076. [Google Scholar] [CrossRef]
- Pereira, F.M.V.; Colnago, L.A. Determination of the Moisture Content in Beef without Weighing Using Benchtop Time-Domain Nuclear Magnetic Resonance Spectrometer and Chemometrics. Food Anal. Meth. 2012, 5, 1349–1353. [Google Scholar] [CrossRef]
- Pereira, F.M.V.; Pflanzer, S.B.; Gomig, T.; Gomes, C.L.; de Felicio, P.E.; Colnago, L.A. Fast Determination of Beef Quality Parameters with Time-Domain Nuclear Magnetic Resonance Spectroscopy and Chemometrics. Talanta 2013, 108, 88–91. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Pereira, F.M.V.; Rebellato, A.P.; Pallone, J.A.L.; Colnago, L.A. Through-Package Fat Determination in Commercial Samples of Mayonnaise and Salad Dressing Using Time-Domain Nuclear Magnetic Resonance Spectroscopy and Chemometrics. Food Control 2015, 48, 62–66. [Google Scholar] [CrossRef] [Green Version]
- Mangamana, E.T.; Cariou, V.; Vigneau, E.; Kakaï, R.L.G.; Qannari, E.M. Unsupervised multiblock data analysis: A unified approach and extensions. Chemom. Intell. Lab. Syst. 2019, 194, 103856. [Google Scholar] [CrossRef]
- Westerhuis, J.A.; Kourti, T.; MacGregor, J.F. Analysis of multiblock and hierarchical PCA and PLS models. J. Chemom. Soc. 1998, 12, 301–321. [Google Scholar] [CrossRef]
- Biancolillo, A.; Næs, T. The Sequential and Orthogonalized PLS Regression for Multiblock Regression: Theory, Examples, and Extensions. In Data Handling in Science and Technology; Elsevier: Amsterdam, The Netherlands, 2019; pp. 157–177. [Google Scholar]
- Nørgaard, L.; Saudland, A.; Wagner, J.; Nielsen, J.P.; Munck, L.; Engelsen, S.B. Interval partial least-squares regression (i PLS): A comparative chemometric study with an example from near-infrared spectroscopy. Appl. Spectrosc. 2000, 54, 413–419. [Google Scholar] [CrossRef]
- Wold, S.; Johansson, E.; Cocchi, M. PLS—Partial least-squares projections to latent structures, 3D QSAR in drug design. In Theory Methods and Applications; ESCOM Science Publishers: Leiden, The Netherlands, 1993. [Google Scholar]
- Filzmoser, P.; Gschwandtner, M.; Todorov, V. Review of sparse methods in regression and classification with application to chemometrics. J. Chemom. 2012, 26, 42–51. [Google Scholar] [CrossRef]
- Soares, S.F.C.; Gomes, A.A.; Araujo, M.C.U.; Galvão Filho, A.R.; Galvão, R.K.H. The successive projections algorithm. Trends Anal. Chem. 2013, 42, 84–98. [Google Scholar] [CrossRef]
- Roger, J.M.; Palagos, B.; Bertrand, D.; Fernandez-Ahumada, E. CovSel: Variable selection for highly multivariate and multi-response calibration: Application to IR spectroscopy. Chemom. Intell. Lab. Syst. 2011, 106, 216–223. [Google Scholar] [CrossRef] [Green Version]
- Biancolillo, A.; Liland, K.H.; Mage, I.; Næs, T.; Bro, R. Variable selection in multi-block regression. Chemom. Intell. Lab. Syst. 2016, 156, 89–101. [Google Scholar] [CrossRef]
- Biancolillo, A.; Marini, F.; Roger, J.M. SO-CovSel: A novel method for variable selection in a multiblock framework. J. Chemom. 2019, 34, e3120. [Google Scholar] [CrossRef]
- Roeder, S.B.W.; Fukushima, E. Experimental Pulse NMR: A Nuts and Bolts Approach. Addison-Wesley Read. Mass. 1981, 198, 207. [Google Scholar]
- Roger, J.M.; Chauchard, F.; Bellon-Maurel, V. EPO–PLS external parameter orthogonalisation of PLS application to temperature-independent measurement of sugar content of intact fruits. Chemom. Intell. Lab. Syst. 2003, 66, 191–204. [Google Scholar] [CrossRef] [Green Version]
- Miskandar, M.S.; Man, Y.C.; Yusoff, M.S.A.; Rahman, R.A. Quality of margarine: Fats selection and processing parameters. Asia Pac. J. Clin. Nutr. 2005, 14, 387. [Google Scholar] [PubMed]
- Jackson, J.E.; Mudholkar, G.S. Control procedures for residuals associated with principal component analysis. Technometrics 1979, 21, 341–349. [Google Scholar] [CrossRef]
- Nascimento, P.A.M.; Barsanelli, P.L.; Rebellato, A.P.; Pallone, J.A.L.; Colnago, L.A.; Pereira, F.M.V. Time-Domain Nuclear Magnetic Resonance (TD-NMR) and chemometrics for determination of fat content in commercial products of milk powder. J. AOAC Int. 2017, 100, 330–334. [Google Scholar] [CrossRef]
- USDA. Analytical Chemistry Laboratory Guidebook: Residue Chemistry; U.S. Department of Agriculture: Washington, DC, USA, 1991.
- Lawson, C.L.; Hanson, R.J. Solving Least Squares Problems; Prentice Hall: Englewood Cliffs, NJ, USA, 1974; p. 61. [Google Scholar]
- Parker, R.L.; Song, Y.Q. Assigning Uncertainties in the Inversion of NMR Relaxation Data. J. Magn. Reson. 2005, 174, 314–324. [Google Scholar] [CrossRef]




| Type | #Samples | Mean Fw (%) | Min Fw (%) | Max Fw (%) |
|---|---|---|---|---|
| Butter | 35 | 82.5 | 81.5 | 84.9 |
| Margarine | 3 | 79.6 | 78.3 | 80.6 |
| Concentrated fat | 12 | 99.4 | 98.1 | 99.9 |
| T (°C) | #LVT1LT1S | RMSEC (%) | RMSECV (%) | RMSEP (%) | SEP(%) | Bias (%) | (%) | ||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| T1L | PLS | 6 | 6 | 1.05 | 0.98 | 1.33 | 0.97 | 1.15 | 1.14 | −0.18 | 0.55 |
| 15 | 7 | 1.12 | 0.98 | 1.32 | 0.97 | 1.29 | 1.24 | −0.36 | 0.61 | ||
| CovSel | 6 | 7 | 1.00 | 0.98 | 1.33 | 0.97 | 1.22 | 1.20 | −0.21 | 0.63 | |
| 15 | 8 | 1.11 | 0.98 | 1.32 | 0.97 | 1.33 | 1.28 | −0.37 | 0.73 | ||
| T1S | PLS | 6 | 2 | 4.60 | 0.61 | 5.01 | 0.54 | 4.61 | 4.50 | 1.01 | 0.60 |
| 15 | 2 | 3.91 | 0.71 | 4.31 | 0.66 | 5.20 | 5.20 | 0.22 | 0.67 | ||
| CovSel | 6 | 2 | 4.64 | 0.60 | 5.03 | 0.53 | 4.60 | 4.53 | 0.83 | 0.61 | |
| 15 | 2 | 3.93 | 0.71 | 4.30 | 0.66 | 5.27 | 5.27 | 0.17 | 0.69 | ||
| SO−PLS | 6 | 61 | 0.77 | 1.00 | 0.96 | 0.99 | 0.68 | 0.68 | −0.04 | 0.32 | |
| 15 | 72 | 0.81 | 0.99 | 1.11 | 0.99 | 1.00 | 0.95 | −0.32 | 0.47 | ||
| SO−CovSel | 6 | 71 | 0.79 | 0.99 | 1.05 | 0.99 | 0.77 | 0.77 | −0.08 | 0.41 | |
| 15 | 81 | 0.89 | 0.99 | 1.16 | 0.99 | 0.92 | 0.89 | −0.23 | 0.45 | ||
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Roger, J.-M.; Garcia, S.M.; Cambert, M.; Rondeau-Mouro, C. Multiblock Analysis Applied to TD-NMR of Butters and Related Products. Appl. Sci. 2020, 10, 5317. https://doi.org/10.3390/app10155317
Roger J-M, Garcia SM, Cambert M, Rondeau-Mouro C. Multiblock Analysis Applied to TD-NMR of Butters and Related Products. Applied Sciences. 2020; 10(15):5317. https://doi.org/10.3390/app10155317
Chicago/Turabian StyleRoger, Jean-Michel, Silvia Mas Garcia, Mireille Cambert, and Corinne Rondeau-Mouro. 2020. "Multiblock Analysis Applied to TD-NMR of Butters and Related Products" Applied Sciences 10, no. 15: 5317. https://doi.org/10.3390/app10155317
APA StyleRoger, J. -M., Garcia, S. M., Cambert, M., & Rondeau-Mouro, C. (2020). Multiblock Analysis Applied to TD-NMR of Butters and Related Products. Applied Sciences, 10(15), 5317. https://doi.org/10.3390/app10155317