2.1. Model of the System
In the paper, a holonomic mobile humanoid manipulator, working in an industrial environment, was considered. The robot was inspired by the Rollin’ Justin robot [
19], developed by the German Aerospace Center (DLR), which is made up of a humanoid dual-arm upper body, mounted on a mobile platform. In contrast to the original design, the robot proposed in this work was equipped with a holonomic
-type platform with two pairs of Mecanum wheels and the arms with four DOF. The model of the humanoid manipulator on its holonomic platform is shown in
Figure 1. As can be seen, the robot consists of four main components:
The 3DOF holonomic platform, which allows any position and orientation to be achieved in the -plane of the workspace;
The 3DOF torso with three revolute joints and an additional, passive revolute joint, placed at the end of the kinematic chain, ensuring that the chest is always kept orthogonally to the ground;
Two arms, each with 4DOF.
In the work here presented, and for the sake of simplicity and in order to increase the readability of the presentation, the orientation of the end-effectors was not taken into account. Such an assumption does not affect the generality of the presented approach because the proposed method did not limit the number of arm joints, so it is possible to complement the arms with additional 3DOF grippers. The problem with planning a grasping action is beyond the scope of this work; however, it is the subject of ongoing research, and the results presented in such as [
23] can be utilized when considering the humanoid manipulator in this paper.
It was assumed that the humanoid robot consisted of a series of rigid bodies connected by rigid joints. In this case, the location of each link with respect to a previous link can be easily described by the location, i.e., the position and orientation of the local coordinate frame, attached rigidly to the chosen link, relative to the local coordinate frame attached to the previous link. In order to describe the position of the two end-effectors, i.e., the left and right arms of the robot, in the workspace, modified Denavit–Hartenberg (DH) notation [
24] was used, and the parameters of the robot joints and links were determined and are shown in
Table 1.
are the lengths of the humanoid links for the torso and the left and right arms, respectively.
are the joints angles of the torso.
is the joint angle of the last joint of the torso and is used to compensate the rotations of the two previous joints.
are the joint angles of the left and right arms, respectively. The rotation axes of the independent joints of the torso (i.e., the axes for the first, second, and third joints) and all joint axes of left arm are shown in
Figure 1; the rotation axes of the right arm are similar. As shown, the arms are located at the end of the torso, and their bases are rotated by an angle of
. The grippers are located at distances
and
from the fourth joints of the left and right arm, respectively.
The position and orientation of the holonomic platform is uniquely defined by three parameters:
x and
y determine the platform center location in the
plane, and
describes the platform orientation. Finally, the configuration of the four main parts of the humanoid can be described by four vectors:
while the configuration of the whole robot is described by the
n-element vector of the generalized coordinates (in this case,
).
Using the coordinate vector (
1) and the parameters of the robot collected in
Table 1, it is possible to determine the kinematic model of the system
, describing the positions of the end-effectors in the workspace, which can be written in compact form, as follows:
where
is the vector with the positions of the humanoid end-effectors expressed in the workspace global frame,
m is the dimension of the robot task, and
are the functions describing the positions of the left and right end-effectors.
The linear velocities of the end-effectors are given by differential kinematics as:
where
is the vector containing the linear velocities of the end-effectors,
is the vector of the generalized velocities of the robot joints, and
is the
-dimensional Jacobian matrix of the humanoid manipulator, which can be written as:
where
,
,
,
.
Considering the transportation task, it is necessary to take into account the model of the object transported by the robot. In this work, it was assumed that the object was rigid and connected to the end-effectors of the robot. In this case, the location of the object in the workspace can be described by the 6-element vector
:
where
and
are the 3-element vectors describing the position and orientation of the local frame in the workspace global frame. The method does not limit the choice of the origin of the object coordinate frame, so it can be attached to the object at any given point.
2.2. Formulation of the Problem
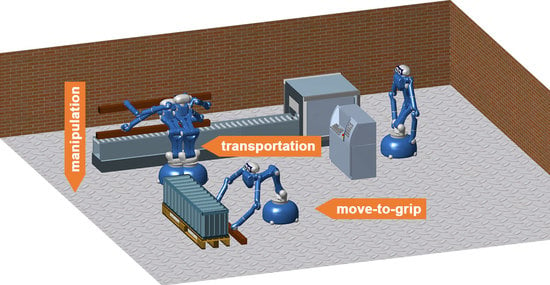
From the perspective of Industry 4.0, the use of information from the integral sensors of the robot, as well as from the sensors located in its surroundings allows tasks that, formerly, had to be planned in detail to now be completed autonomously. The basic idea of a task-motion-planning system for the task of autonomous robot considered in this work is presented in
Figure 2. Such a system consists of the Task Planner, which specifies the main goals for the robot based on information from the sensors, and the Motion Planner, which plans the robot motion, according to the goals from the Task Planner. Trajectories generated by the Motion Planner are transmitted to the Robotic System. In the presented work, it was assumed that the information from the Task Planner was known and only the subsequent phases of the transportation problem of the lengthy object, as represented by blue boxes in the diagram, remained to be considered.
According to the idea of the Motion Planner, presented in
Figure 2, the considered task of a humanoid mobile manipulator transporting an object in an industrial environment is divided into three phases (subtasks), solved separately:
Moving the end-effectors to the given location starting from the current configuration in order to approach the object to be moved;
Moving the object to the specified location in the workspace;
Moving the object along a prescribed path in order to complete a precise operation, such as an assembly task.
The first task was to move the end-effectors of the humanoid manipulator to the grip points specified by the Task Planner. This is a common, point-to-point task, in this case, to be undertaken by two end-effectors simultaneously. It can be expressed as:
where
T is the final moment of the motion and
is the
-element vector containing the final position of the left
and the right
end-effectors of the robot.
In the second and third task, it is necessary to take into account the object being transported by the robot. In the presented work, such tasks were formulated as the movement of the object in the workspace, where the motion of the robot was forced by the set of constraints resulting from the closed kinematic chain established by the robot arms and the object being held by them. In both cases, the robot began the movement from the initial configuration holding the object; however, in the second task, achieving the desired final location was the only goal of any importance, while in the third task, the movement of the object was determined by the prescribed path .
In the second task, starting from the configuration achieved in the first one, the robot moved the object being transported to the position specified by the Task Planner. According to the above considerations, this task can be described as:
Finally, the humanoid manipulator started from the final configuration of the previous task and carried out the precise manipulation of the object, according to the path determined by the Task Planner. Such a task can be written as follows:
where
s is the scaling parameter, which depends on time
t, i.e.,
,
.
In both of the above cases, additional constraints resulting from grasping should be considered. The humanoid manipulator held the object at two contact points, and the hard finger model [
25] of contact was assumed in this paper. This assumption means that the linear components of the velocities were transmitted through the contact point, while, on the other hand, the angular components were not. Introducing the function
, describing the locations of the contact points, the grasp limitations can be expressed as geometric and kinematic constraints as follows:
where
describes the linear velocities of the contact points.
The practical processes that are accomplished by the industrial robots impose some conditions at the beginning and the end of the trajectory. It is natural to assume that at the initial and final moments of the performance of the task, the velocities of the manipulator equal zero:
During the completion of the task, the robot should maintain the limitations resulting from its construction and the range of movements permitted in the individual joints. Introducing the scalar function
, defining the algebraic distance of a given configuration from the range permitted, such mechanical constraints can be expressed in the form of a set of
inequalities in the form:
The space in which the robot operates may contain some equipment that should be treated as obstacles and must be taken into account during the motion planning. Introducing the scalar functions
and
, which describe the algebraic distances from the obstacles to the robot and object, respectively, the collision avoidance conditions can be written as sets of
for the robot and
for the object inequalities in the form:
In practice, the configuration of the manipulator joints should be far away from singular configurations. In order to achieve this goal, the Yoshikawa manipulability measure [
26], which describes the distance to singular configurations, may be maximized. The Yoshikawa manipulability index
is proportional to the volume of the velocity ellipsoid. The semi-axes of this ellipsoid coincide with the eigenvectors of the matrix
, the lengths of these semi-axes being equal to the square roots of the eigenvalues of
. Since the product of the lengths of the semi-axes is proportional to the volume of the ellipsoid and the product of the eigenvalues of the matrix is equal to the determinant of the matrix, the manipulability measure may be calculated as:
. It seems that in the case of a dual-arm humanoid manipulator, the avoidance of singular configurations of the robot arms [
27] is important, so the following manipulability measure was taken into account:
where
consists of the 8 last columns of the matrix (
4).
2.3. Solution: Primary Tasks
According to the analysis from the previous section, the transportation task, considered in this work, consisted of three steps: moving the robot to the object, moving the object to a specific location, and moving the object along a prescribed path. The first step is a point-to-point task described by the dependency (
6). In the presented approach, in order to eliminate, known from the literature, the drift effect resulting in a trajectory error increasing in time, a feedback loop algorithm, correcting the robot movement on the basis of the information from the sensors, was proposed. For this purpose, the following end-effector error function
between the current and fixed final end-effectors positions was introduced:
Using this function, the task of the robot can be presented in a more general form as:
Such a formulation of the task allows reaching the final positions of the end-effectors, in a finite time, with any accuracy defined by the needs of the realized process. Moreover, in the proposed solution, the convergence rate and resulting final time were dependent on the gain coefficients and these can be tuned by their appropriate selection.
In order to solve the trajectory planning problem of the humanoid manipulator, the following system of differential equations was introduced:
where
and
are
diagonal gain matrices with positive coefficients, which determine the convergence rate of the solution of Equation (
17).
The system (
17) is a homogeneous differential equation with constant coefficients. In order to find the solution,
consistent dependencies should be given. They can be determined from the error function (
15) for
, taking into account the initial condition (
10). Moreover, using the Lyapunov stability theory and an approach similar to that presented in [
28] for nonholonomic mobile manipulators, it is possible to show that the system is asymptotically stable, so the end-effector error
and its derivative
converge to zero, guaranteeing fulfillment of the conditions (
16). The convergence rate depends on the gain coefficients of matrices
and
.
Determining the components
,
as:
and substituting them into System (
17), the dependency that allows determining the trajectory of the humanoid can be written as:
where
.
The dependency (
19) formulates the primary task of the humanoid manipulator, which grasps the object in the locations specified by vector
. Due to the high redundancy of the humanoid
, the Jacobian matrix
is rectangular (the number of its columns is greater than the number of its rows), and there is an infinite number of trajectories satisfying the condition (
19). In order to find solution
, the task can be formulated as a quadratic optimization problem with linear constraints, which leads to the determination of a trajectory minimizing a certain cost. Using the Moore–Penrose pseudoinverse of matrix
,
, the optimal solution minimizing the acceleration norm of a mobile robot
and satisfying the linear constraints (
19) can be determined as:
The dependency (
20) describes the trajectory realizing the primary task of a humanoid robot. The additional constraints imposed on the robot motion, as presented in the previous section, will be introduced as secondary objectives in the next section.
In the second step of the transportation task, the robot moves the object to the desired location
. In order to solve this task, in the presented work, the method of trajectory planning for the object, guaranteeing fulfilling the dependency (
7), while simultaneously determining suitable robot movement, was proposed. In this case, the object was considered as the single 6DOF joint, which can achieve any position and orientation in a 3-dimensional workspace, and its movement was planned using an idea similar to that used in a previous task. For this purpose, the following function
describing the error between the current and desired fixed location of the object was introduced:
and this task can be formulated as:
Similarly, as in the case of the trajectory planning in the move-to-grip phase (
22), such a formulation of the object task would allow achieving the desired location of the transported object with any accuracy in finite time.
Introducing the
diagonal matrices with positive coefficients
and
, the trajectory of the object can be determined from the following equation:
with respect to the initial conditions determined from (
21) for
and zero initial velocity of the object resulting from the lower condition (
9) and (
10). The stability of Equation (
23) is assured by the assumed form of the gain matrices, guaranteeing the fulfillment conditions (
22). Finally, similar to the previous task, after determining
,
and using the simple algebra, the trajectory of the object can be written as:
Taking into account that the transported object is rigid and that the location of the grip points in the object frame is known (this was determined by the Task Planner), the location of the grip points in each time instant can be calculated using function . According to the proposed approach, the trajectory of the contact points, determined in this way, defines the trajectory tracking task to be performed by the robot in this phase.
In order to ensure suitable robotic movement, enabling the desired location of the object determined from (
24) to be reached, the grasp limitations (
9) must be satisfied, so the primary task of the robot, after introducing end-effector error
:
may be formulated as:
The trajectory of the robot, as in the case of the point-to-point task, can be determined from differential Equation (
17) for a new form of error function introduced by the dependency (
25) as follows:
where
.
Due to the asymptotic stability of the differential Equation (
17) and assuming that the initial condition (
10) and the grasp limitations (
9) at the initial moment of the motion are fulfilled (the robot is motionless and holds the object at contact points
, so
and
), the error function
and
at each instant, which guarantees the fulfillment of the grasp limitations while the robot is moving.
The task realized in the third step is similar to the second one, but the position and orientation of the object during the whole movement is given by the path
, preplanned earlier by the Task Planner, as shown in
Figure 2. It was assumed that the path was given in parametric form as a function of scaling parameter
s, dependent on time. In this case, the error function describing the distance between the current location of the object and the location determined by the path, extended by an additional element responsible for tracing the entire path, was introduced as follows:
Using this function, the third task (
8) can be described in a more general form as:
Similarly, as in the first and second phase of the transportation task, such a formulation of the path tracking problem will allow achieving the final location of the object path with any accuracy. Moreover, if the object is not positioned precisely at the beginning of the path, the tracking error
will converge to zero during the object movement. Finally, the object trajectory and the path parameterization can be determined using the following system of differential equations:
where the gain matrices
and
were accepted in the same way as in the second task and ensure the asymptotic stability of the first equation, and
and
are the positive scalars, which provide the asymptotic stability of the second equation. The property of the stability of Equation (
30) implies the fulfillment of the conditions (
29); moreover, if in the initial moment of motion,
and
(the object is located at the beginning of the path, and
), the object will be moved along the path for the whole process.
Finally, after simple calculations, the trajectory of the object
and the path parameterization
can be determined from (
30), in a manner similar to the previous tasks, using the initial conditions obtained from (
28) for
as follows:
The manner for establishing the trajectory of the humanoid manipulator is the same as for the second task, so the trajectory of the robot is given by the dependency (
27). Additionally, let us note that a similar approach, i.e., the motion along the given path, can be used to plan the grip of the object at the end of the move-to-grip phase.
2.4. Solution: Secondary Tasks
Due to its structure, the mobile humanoid manipulator has a high degree of redundancy, i.e., it has more degrees of freedom than are needed to perform the considered tasks. The existence of additional degrees of freedom makes it possible to introduce additional criteria that allow the manner in which the humanoid manipulator carries out the task to be determined. In such a case, a conflict between the primary task and additional limitations is possible. The problem can be solved by prioritizing individual tasks that will allow secondary goals to be achieved only if they do not violate the primary task. In a typical approach, the robot task was treated as the primary objective function, and additional conditions were included as secondary functions.
The tasks of the robot and the requirements determining how they are carried out are defined by the constraints introduced in the problem formulation section. The constraints imposed on the end-effector movement (
6)–(
9) specify the primary tasks of the robot and were taken into account along with the initial condition (
10) in the solution presented in the previous section. The remaining limitations must be considered as secondary objectives of the tasks. In particular, as was shown in [
29], the zero velocity of the end-effectors in the destination location, assured by the solution of the primary task, does not guarantee that the robot motion will come to a stop, once the task has been accomplished, thus satisfying the condition (
10). In the case of the Jacobian pseudoinverse methods, it is important to provide the high manipulability measure of the robot (
14) to avoid the loss of the Jacobian matrix rank. Moreover, the high manipulability in the destination location makes it easier to complete the next task. Finally, in practical applications, it is essential to fulfill the constraints resulting from the mechanical properties of the robot (
11), as well as to avoid collisions during the robot motion in an industrial environment (
12).
In order to fulfill the secondary objectives of the task, the following dependency, resulting from the
properties
, where
is the identity matrix, was used. The right multiplication of this dependency by
gives:
where
is the projection matrix on the null space of
, and as a result, if
is a solution of the primary task of the robot, then for any chosen vector
, the solution of this task is also a vector:
Finally, it may be concluded that vector
, projected by operator
, allows the configuration of the robot to be changed without changing the positions of its end-effectors, so it may be used to satisfy the secondary objectives of the task [
30]. This approach leads to a solution of the mobile robot in the following form:
By choosing vector
in such a way as to optimize some additional criterion, it is possible to take into account a secondary objective in the form
. According to [
30], mapping
is usually taken as a mixed objective function:
whose minimization leads to a reduction in the velocities of the mobile robot and the fulfillment of the additional criteria described by mapping
. In this work, this additional term was used to maximize the manipulability measure and to satisfy the collision and mechanical constraints. For this purpose, function
was taken as:
where
is the manipulability measure given by the dependency (
14),
denotes any continuous and differentiable internal penalty function, which increases when the robot approaches the obstacle surface, thus allowing the inequality constraints (
12) to be fulfilled, and
is any continuous and differentiable function, which leads to the maximization of the distance of the configuration variables from the limits of the allowed range, resulting from the inequality constraints (
11).
In order to find a solution of the robot task minimizing the criterion (
34) and (
35), the approach presented in [
30], based on the steepest descent method, may be used, and vector
can be written in the following form:
where
is a positive defined scalar describing the influence of the second term.
The approach presented above can be used for all types of humanoid manipulator tasks, supplementing the solutions (
20) and (
27) according to the dependency (
33). It is worth noting that the proposed solution is pure kinematic at the acceleration level and does not take into account the dynamic properties of the robot. However, such an approach does not preclude practical applications of this method. Considering the physical capabilities of the robot actuators and the mass of the transported object, it is possible to determine suitable mechanical limitations that allow a real robot to perform the task. Moreover, the advantage of the kinematic approach is the lower computational burden of the algorithm.
In the case of the second task, planning the trajectory of the object was additionally required. The collision-free movement of the robot does not guarantee the collision-free movement of the object, so the object trajectory (
24) must also take into account the conditions for avoiding collisions. The transported object did not have redundant degrees of freedom, so in this case, the avoidance of collisions cannot be performed using the secondary objective functions’ approach. On the other hand, in the second task, the final location was specified only, and the object can make any movement during the task execution. This makes it possible to take into account the conditions for avoiding collisions and supplementing the trajectory of the object (
24) by the perturbation of the object accelerations in the neighborhoods of the obstacles. Finally, the trajectory of the object was proposed as:
where
, as with the avoidance of collisions of the robot, denotes any continuous and differentiable internal penalty function, which takes the value 0 when the object is outside the zone surrounding the obstacle and increases when it approaches its surface, allowing the inequality constraints (
13) to be fulfilled.
Let us note that in the third task, the object moved along the path preplanned by the Task Planner and did not collide with any obstacle in the workspace by definition, so the trajectory (
31) did not require any modification.