High-Power Continuous-Wave Directly-Diode-Pumped Fiber Raman Lasers

Abstract

We describe novel fiber Raman lasers pumped directly by spectrally combined high power multimode laser diodes at ∼975 nm and emitting at ∼1019 nm. With a commercial multimode graded-index fiber, we reached 20 W of laser output power with a record slope efficiency of 80%. With an in-house double-clad fiber, the beam quality improved to $M^2$ = 1.9, albeit with lower output power and slope efficiency due to higher fiber loss. We believe this is the first publication of a fiber Raman laser cladding-pumped directly by diodes.

1. Introduction

Fiber lasers have become leading candidates in the high power regime thanks to advantages over traditional solid-state lasers such as gain efficiency, compactness, ruggedness, and flexibility. Generally, these are pumped by diode lasers, which are very efficient converters from electrical to optical energy [1]. Ytterbium-doped fiber (YDF) lasers emitting around 1 μm work particularly well, and have reached 20 kW of output power with excellent beam quality [2]. However, rare-earth doped fibers emit in fixed spectral bands and require that the diode laser emission spectrum overlaps with their absorption bands. By contrast, fiber Raman lasers (FRLs) are a wavelength-agile alternative for producing gain and power with optical fiber. In these, the emission wavelength is determined by the pump wavelength and the Raman shift, which can be one or several Stokes orders, and is restricted by the transparency range of the fiber rather than by the spectral bands of stimulated emission [3,4]. In addition, FRLs possess the potential for low quantum defect. This becomes smaller at shorter wavelengths, relative to the pump photon energy [5]. Other properties that can be used to overcome limitations of rare-earth-doped fiber sources are instantaneous pump-to-Stokes conversion and immunity to self-Q-switching. Photodarkening is another problem with Yb-doped fibers [6]. This can occur also in FRLs, especially with highly germanium-doped fibers (as often used for FRLs), operating at visible wavelengths at high power densities. Thus, for example, photodarkening is known to occur in fibers used for supercontinuum generation at visible wavelengths [7]. However, at longer wavelengths and lower power densities for Raman conversion in fibers longer than 100 m, we expect photodarkening to be negligible. Furthermore, cladding-pumped Raman gain fibers, similarly to conventional rare-earth-doped fibers, can enhance the brightness when a multimode (MM) optical pump beam is transformed into an output with better beam quality [8,9].

Power-scaling of FRLs has been the subject of much research, but typically with diode-pumped rare-earth-doped fiber lasers used as pump sources [10]. As an example, a YDFL-pumped fiber Raman laser reached 1.3 kW of CW output power at 1120 nm with high overall conversion efficiency [11]. Still, the use of a two-stage pumping scheme makes the FRLs more complex and is only practical for certain wavelengths. Furthermore, the intermediate pump source is often diffraction-limited. Further conversion in a FRL will then degrade the brightness, and is therefore counter-productive when brightness is our primary concern.

It is also possible to pump the FRL directly with diodes. This eliminates the intermediate conversion stage, and furthermore benefits from the wide wavelength coverage available from diodes. This includes wavelengths not covered by alternative practical pump sources, e.g., in the 800–1000 nm range. However, despite these attractions, power-scaling of diode-pumped FRLs has been held back by the high pump densities and low fiber propagation losses that are needed to reach laser threshold, since stimulated Raman scattering (SRS) is a weak process. Diode-pumping has been restricted to single-mode devices operating at around 1.5 μm [12]. These benefit from the high brightness of single-mode laser diodes and low fiber loss. However, the power of single-mode diodes is limited to the watt-level or less, and multimode diodes in this wavelength range lack in brightness and are much lower in power and efficiency than what is possible at shorter wavelengths. While FRLs pumped by MM diodes have been demonstrated recently at wavelengths as short as 0.8 μm [13], the high fiber loss meant that the required pump brightness could only be reached in pulsed mode, which restricted the average power. For power-scaling of FRLs, lower fiber loss and superior cw brightness and power make 0.9–1 μm diodes a better choice, and devices based on MM pumping of MM fibers have recently been demonstrated [14]. However, these still operated relatively close to threshold, with output power of 3 W and slope efficiency of 35% or less. Furthermore, while some beam quality improvement (beam cleanup) is possible in MM FRLs, the beam quality was still far from that obtained with double-clad fibers, which can readily generate diffraction-limited output.

In this paper, we present results with an improved pumping system that allows us to operate higher above threshold and with fibers with higher loss than in our previous work [15]. We reached a record output power of 20 W at 1019 nm and a slope efficiency of 80%, in a comparatively short piece of a commercial MM fiber with low total propagation loss. However, the output was multimode. In order to improve the beam quality, we also used a double-clad Raman gain fiber, and obtained an output power of 6 W and a slope efficiency of 19%. The efficiency is lower because the loss of this fiber, fabricated in-house, is higher than that of state-of-the-art commercial MM fiber. Nevertheless, thanks to an improved beam quality ($M^2$ = 1.9), the brightness improved by a factor of 9.6 over that of the pump beam. We believe this is the first fiber Raman laser cladding-pumped directly by diodes. Finally, we estimate the improvements possible with optimized and lower-loss laser configurations, as well as with improved Raman gain fibers and pump sources.

2. Multimode Raman Gain Fiber

To improve a fiber Raman laser one can improve the fiber, the cavity, or the pump source. We first investigated improvements possible with the same graded index multimode (GRIN-MM) fiber (OFS OM-4) we used before [15], in a similar cavity, but with a better pump source. For this, we spectrally combined two wavelength-stabilized pigtailed MM diode sources (IPG Photonics, PLD-70-975-WS). Each source can deliver 45 W of power from a 0.11 mm diameter core with an NA of 0.12. The diodes are spectrally offset from each other, at 974.6 nm and 975.1 nm, with linewidth of ∼0.5 nm (full width at half maximum, FWHM). The output beams were collimated and then combined into a single beam in an angled narrow-band volume Bragg grating (VBG, Optigrate model C38-48-C1) as shown in Figure 1. The VBG has an aperture of $5\times 2$ mm, a thickness of 5 mm, and a FWHM bandwidth of 0.43 nm. The reflection efficiency for the 975.1 nm diode was ∼70%, and the transmission efficiency for the 974.6 nm diode was ∼80%. We reached 70 W of combined power (Figure 1b), without discernable degradation of the beam quality.

Figure 1. (a) Experimental setup of the spectrally beam-combined diode pump source; (b) Reflected and transmitted pump power after VBG vs. input power of each diode.

Figure 1. (a) Experimental setup of the spectrally beam-combined diode pump source; (b) Reflected and transmitted pump power after VBG vs. input power of each diode.

The wavelength-combined pump light was launched into the multimode Raman gain fiber via a lens as shown in Figure 2. The launch efficiency was 60%. The Raman gain fiber has a germanosilica core with diameter of 62.5 μm (area ∼3070 μm${}^2$) and profile as shown in the inset of Figure 2. The numerical aperture is 0.275, which corresponds to a peak refractive-index difference to the pure-silica cladding of 0.026. From this, the Raman gain coefficient $g_R$ can be estimated to $1.19\times {10}^{-13}$ m/W in the center of the core for unpolarised light at 975 nm [10,11]. The propagation loss was measured to 1.7 dB/km at the pump wavelength and 1.5 dB/km at the Stokes wavelength of 1019 nm. We used two lengths of fiber, 3 km and 1.5 km. The effective lengths ($L_{eff}$), as determined by the actual length and the pump propagation loss, become 1.8 km and 1.1 km, respectively.

In the far end of the fiber, a lens-coupled dichroic mirror (DM) with reflectivity of over 99% for both of pump and Stokes, was used to launch escaping light back into the fiber with 80% launch efficiency. The dichroic mirror has a reduced reflectivity of 5% at the wavelength of the second Stokes around 1064 nm. This helps to prevent SRS to the 2nd Stokes at 1064 nm, which can degrade the conversion efficiency [5]. The fiber had flat normal cleaves in both ends. Thus, the resulting 4% reflectivity closed the laser cavity in the combined pump launch and out-coupling end of the fiber. There, another dichroic mirror separated the out-coupled beam from the pump path. The total roundtrip loss at the Stokes wavelength in the resulting linear laser cavity becomes 24.5 dB and 20.0 dB for the two different fiber lengths of 3 km and 1.5 km, respectively.

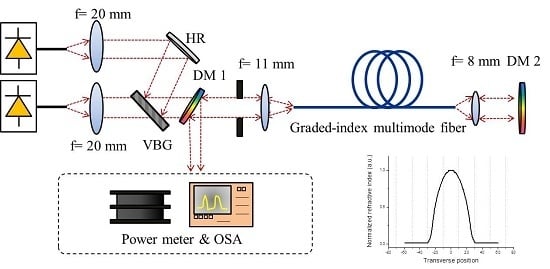
Figure 2. Experimental setup of the CW FRL with GRIN Raman gain fiber. VBG: volume Bragg grating; DM: dichroic mirror; HR: high reflection mirror. Inset: refractive index profile (RIP) through the center of the core of the GRIN MM fiber.

Figure 2. Experimental setup of the CW FRL with GRIN Raman gain fiber. VBG: volume Bragg grating; DM: dichroic mirror; HR: high reflection mirror. Inset: refractive index profile (RIP) through the center of the core of the GRIN MM fiber.

Figure 3 shows the total laser output power measured from the 3 km and 1.5 km long GRIN-MM fibers, together with the results of theoretical calculations. Experimentally, the output power with the 3 km long fiber reached 15 W with a slope efficiency of 62% and a threshold of 16 W. For the 1.5 km long fiber, the threshold increased to 20 W and the slope efficiency increased to 81%, while the output power reached as high as 19 W. This corresponds to a record optical-optical device efficiency of about 50%. We attribute the high power and efficiency to the low loss of the fiber, as well as the high pump brightness, which allows us to operate relatively high above threshold in fibers short enough to further reduce the impact of propagation loss. The thresholds correspond to single-pass gain slopes of 0.82 dB/W (3 km) and 0.50 dB/W (1.5 km).

Figure 3. Simulated and experimental CW FRL output power against the launched pump for GRIN-MM fiber lengths of 3 km (a) and 1.5 km (b).

Figure 3. Simulated and experimental CW FRL output power against the launched pump for GRIN-MM fiber lengths of 3 km (a) and 1.5 km (b).

We measured the beam quality ($M^2$) of the pump incident on the fiber to 22.2, while it became 5.0 for the generated output beam. This means that the brightness (radiance) improved from 0.15 W·sr${}^{-1}$·μm${}^{-2}$ to 0.77 W·sr${}^{-1}$·μm${}^{-2}$, i.e., by a factor of 5.2 with respect to the incident pump beam. These measurements were at maximum power. We note the beam quality can be calculated from the refractive-index profile. In the highly-multimode regime, under the assumption that all modes are equally excited, we calculate the pump $M^2$-value to approximately 15.4 in this fiber, using the approach described in [16,17]. This corresponds to a brightness of the launched pump beam of 0.19 W·sr${}^{-1}$·μm${}^{-2}$ at full power. This slightly higher value than that of the incident pump beam is not surprising, since the launch can be adjusted to select the highest-brigthness parts of the incident beam. The $M^2$-value of the laser output beam would be 14.7 if all modes were equally excited, which is considerably worse than the actual beam quality.

We calculated the thresholds from the cavity losses, core area, effective lengths, and Raman gain coefficient. These become much higher than the measured thresholds, if we assume that the pump was uniformly distributed over the 3070 μm${}^2$ core area. However, the pump intensity is more likely to be higher in the center of the core, where the refractive index is higher. Therefore, the signal will build up there. This reduces the effective area. The precise value depends on which pump and signal modes are involved, but if we assume that all pump modes are uniformly excited then the effective area varies between 1930 μm${}^2$ (if lasing occurs on all modes, if they are strongly coupled) and 1307 μm${}^2$, if lasing occurs on the fundamental mode. The effective area is expected to vary with the power level, since the Stokes wave can selectively deplete pump modes as the Stokes power grows. Different loss of different modes can be a further complication, as is mode coupling occurring along the fiber and at the fiber ends. We adjusted the effective pump area to 1530 μm${}^2$ in order to achieve good agreement with measured data. The power characteristics with two fiber lengths were calculated using appropriate boundary conditions and standard power conversion equations [18]:

$$\begin{array}{c}\hfill \pm \frac{1}{P_p^{\pm }}\frac{P_p^{\pm }}{dz}=-{\alpha }_p-\frac{g_R}{A_{eff}}\frac{{\lambda }_s}{{\lambda }_p}(P_s^{+}+P_s^{-})\\ \hfill \pm \frac{1}{P_s^{\pm }}\frac{P_s^{\pm }}{dz}=-{\alpha }_s+\frac{g_R}{A_{eff}}(P_p^{+}+P_p^{-})\end{array}$$

(1)

Here, subscript p refers to the pump and s to the Stokes wave. The plus and minus signs are used for forward and backward propagating waves, respectively. Furthermore, α is the attenuation constant and λ is the wavelength. $g_R$ refers to the Raman gain co-efficient and $A_{eff}$ is the effective area. Figure 3 shows that with $A_{eff}$ = 1530 μm${}^2$, the simulated characteristics agree with measurements, which confirms the high slope efficiency achievable in the 1.5 km fiber and the importance of the fiber length.

Finally, Figure 4 shows the output spectrum from the 1.5 km fiber at full power. There is no sign of the second Stokes. The emission wavelength was 1019 nm for a Stokes shift of approximately 443 cm${}^{-1}$ and a quantum defect of only 4.3%. The measured linewidth was resolution-limited (2 nm).

Figure 4. Experimental FRL output spectrum at 20 W of laser output power from 1.5 km of GRIN fiber.

Figure 4. Experimental FRL output spectrum at 20 W of laser output power from 1.5 km of GRIN fiber.

3. Double-Clad Raman Gain Fiber

For further improvements of the brightness, there is more potential in improving the beam quality than in improving the conversion efficiency. While it is well-known that SRS can improve the beam quality in GRIN-MM fibers [19], other multimode fiber structures such as double-clad fibers can be more effective in this regard and even produce single-mode output [20]. We therefore designed and fabricated a double-clad Raman gain fiber (DCRF) and evaluated it in a similar experimental setup. However, the loss of the DCRF is considerably higher than that of the commercial GRIN MM fiber, 7.5 dB/km at the pump wavelength and 6.9 dB/km at the Stokes wavelength, for light launched into the combined core and inner-cladding waveguide. It was therefore necessary to further improve the pump source. We replaced the 45 W diodes by ones that can provide 60 W of power from a 105 μm core at an NA of 0.13. The new reflected diode source is wavelength-stabilized at 975.6 nm with ∼0.6 nm linewidth FWHM. The transmitted diode, which is not wavelength-stabilized, has a central emission wavelength in the range of 969.4–971.2 nm and a linewidth of 4 nm.

The un-stabilized diode has higher transmission through the VBG than the previous stabilized one, and can also be taken to slightly higher power than the rated 60 W. When this diode is used on its own, the power through the VBG reaches 54 W. When the other diode is used on its own, the power reflected off the VBG reaches 35 W, which is comparable to the power with 45 W diode. We attribute the decrease in reflection efficiency for the higher-power diode to its larger linewidth. In addition, the increased heating at higher power may perturb the VBG [21]. Figure 5 shows the transmitted and the reflected power from the VBG against the input power from the diodes. The maximum total combined pump power reaches nearly 85 W, compared to 70 W with the lower-power diodes. At the same time, the beam quality degraded from $M^2$ = 22.2 to $M^2$ = 23.2. Thus, the pump brightness improved by 11% over that of the lower-power system, to 0.17 W·sr${}^{-1}$·μm${}^{-2}$.

Figure 5. Reflected and transmitted pump power after VBG with 60-W diodes vs. power incident on the VBG.

Figure 5. Reflected and transmitted pump power after VBG with 60-W diodes vs. power incident on the VBG.

Our DCRF was manufactured in-house with the standard modified chemical-vapor deposition process. It has a pure-silica outer cladding surrounding a raised inner cladding and an embedded core, which are both doped with germanium in different concentrations to create the refractive index profile. The NA of the inner cladding is 0.3 with respect to the outer cladding, while the core-NA is 0.1 with respect to the inner cladding. The inner-cladding and core diameter are, respectively, 38 μm and 14.6 μm, with encircled areas of 1134 μm${}^2$ and 167 μm${}^2$ in the drawn fiber. The inner-cladding-to-core area ratio equals 6.8. This is below eight and therefore small enough to allow for efficient first-Stokes generation [22]. The fiber is protected by a low-index polymer coating, so also the outer cladding can guide light. The core supports two modes at the Stokes wavelength, $L{P}_{01}$ and $L{P}_{11}$. From the core refractive index difference of 0.036 to pure silica, we estimate the Raman gain coefficient to $1.31\times {10}^{-13}$ m/W for unpolarized light at 975 nm.

Figure 6 shows the experimental configuration. In the same manner as for the multimode Raman gain fiber, the wavelength-combined pump beam was launched into the inner-cladding of the DCRF through a DM and a lens with a launch efficiency of ∼76%. A small fraction of the pump light, estimated to be 1.6% was actually guided in the core, while we used high-index gel to strip out any light launched into the outer cladding. The Raman laser cavity comprised 0.65 km of the DCRF as the Raman gain medium and the same lens-coupled DM as before, high-reflection (HR) for pump and 1st Stokes and with ∼ 5% reflectivity for the second Stokes. The fiber was perpendicularly cleaved in both ends. However, because of the higher fiber loss, the resulting 4% feedback in the pump launch end of the cavity was no longer sufficient for lasing to occur. Although not available, a longer fiber could perhaps help to reduce the threshold, but the 0.39 km effective length is already 67% of the limiting case of an infinitely long fiber, due to the relatively high propagation loss of the DCRF. Therefore, we reduced the cavity losses by using an external output coupler. This reflects 60% of the incident power back towards the DCRF via a dichroic mirror that splits the pump and Stokes beam paths.

Figure 6. Experimental setup of the CW FRL with DCRF. VBG: volume Bragg grating; DM: dichroic mirror; HR: high reflection mirror; DCRF: double clad Raman gain fiber.

Figure 6. Experimental setup of the CW FRL with DCRF. VBG: volume Bragg grating; DM: dichroic mirror; HR: high reflection mirror; DCRF: double clad Raman gain fiber.

The output power and spectrum from the FRL are shown in Figure 7. The laser threshold is 33 W, and we obtained a maximum output power of 6 W for 65 W of launched pump power. The laser slope efficiency is 19%. Theoretical power characteristics calculated as for the MM fiber are shown, too. We set the effective area equal to the pump waveguide area (1130 μm${}^2$). This corresponds to a uniform pump distribution across the pump waveguide. We then used the pump and Stokes re-launch efficiencies as fitting parameters in order to obtain good agreement with experimental threshold and output power. The fitted re-launch efficiencies become 64% at the high reflectivity (HR) end and 58% at the out-coupling end. Note that although we would like the Stokes wave to be confined to the core, also the inner cladding guides and amplifies light. Because the germanium content of the inner cladding is slightly smaller, both the Raman gain and propagation loss can be expected to be a little lower, for overall similar laser threshold for cladding-modes. Thus, also cladding-modes can lase with a similar threshold, which means that it is the re-launch losses into the inner cladding rather than into the core that matter, for the Stokes as well the pump.

Although there are uncertainties in the parameters also with the DCRF, the relatively flat refractive-index profile makes the assumption of a uniform pump distribution well motivated, at least in the absence of SRS-induced depletion. While the use of fitting parameters makes the simulations less robust, we still consider the model adequate for quantitative predictions of the influence of parameters such as fiber length.

Figure 7. (a) Experimental FRL output power with DCRF vs. pump power; (b) Experimental FRL output spectrum at 6 W maximum powers with DCRF.

Figure 7. (a) Experimental FRL output power with DCRF vs. pump power; (b) Experimental FRL output spectrum at 6 W maximum powers with DCRF.

The measured output spectrum is free from higher order Stokes light even at the highest output power. Again, the measured linewidth was resolution-limited (2 nm). The output beam quality became $M^2$ = 1.9 and the radiance 1.6 W·sr${}^{-1}$·μm${}^{-2}$ at maximum power (6 W). The brightness enhancement in the case of DCRF was about 9.6 times, compared to the incident pump beam.

4. Discussion

Despite the higher power achieved with the MM GRIN fiber, the radiance is still higher with the DCRF, and nearly ten times higher than that of the pump, thanks to the higher beam quality. This is a key attraction of DCRFs. On the other hand the comparatively high propagation loss of the DCRF used here limits the output power and efficiency. While higher pump power in the fiber (to allow for shorter fibers) as well as lower loss are possible long-term remedies for this, it is also interesting to see what is achievable with the present power-level and fiber. Figure 8 shows how the theoretically calculated output power depends on the length of the DCRF for several out-coupling and re-launch efficiencies. With 100% re-launch efficiency; it is theoretically possible to reach over 62% conversion efficiency with 1% out-coupling as shown in Figure 8a. This improvement is possible thanks to a fiber sufficiently short (∼2 m) to make pump propagation losses negligible. Although the Stokes power of almost ∼4 kW circulating in the cavity (present in each direction) may be unrealistic, similar efficiencies are possible with, e.g., 10% out-coupling, 12 m of fiber, and ∼400 W of circulating Stokes power with 100% re-launch efficiency as shown in Figure 8a.

An output coupling of 40%, which is more typical for a fiber laser, still allows for 57% conversion efficiency with 92 W of circulating Stokes power in 60 m of fiber as shown in Figure 8b. However, with the 96% of out-coupling from a perpendicularly cleaved fiber facet, the conversion efficiency is reduced to 28% with our parameters, even if there are no re-launch losses as shown in Figure 8b. This is due to increases in threshold and propagation losses as the optimum fiber length increases to nearly 400 m.

Figure 8. (a) Simulations of the output power vs. DCRF length at pump power of 65 W (launched) for out-coupling ratio (R1) of 0.9 and 0.99 and for 100% re-launch efficiencies for pump as well as Stokes wave in both ends of the cavity; (b) Simulations of the output power vs. DCRF length at pump power of 65 W (launched) for various out-coupling ratio (R1) and 100% re-launch efficiencies.

Figure 8. (a) Simulations of the output power vs. DCRF length at pump power of 65 W (launched) for out-coupling ratio (R1) of 0.9 and 0.99 and for 100% re-launch efficiencies for pump as well as Stokes wave in both ends of the cavity; (b) Simulations of the output power vs. DCRF length at pump power of 65 W (launched) for various out-coupling ratio (R1) and 100% re-launch efficiencies.

In reality, the re-launch losses may well be significant (as they were in our experiments). Figure 9 shows several curves indicating the output powers which are possible with different re-launch and out-coupling ratios with 65 W of launched pump power. Figure 9 also contains data calculated with the re-launch efficiencies of 64% at the high reflectivity end and 58% at the out-coupling end as suggested by our curve-fitting to the experimental data of the DCRF. The output power becomes 6 W for the 650 m of fiber we used. This improves to ∼12 W, at the optimum fiber length of ∼200 m. Reduced re-launch losses allow for much larger improvements, as exemplified with several curves in Figure 8 and Figure 9.

Figure 9. Simulation of output power vs. DCRF length at pump power of 65 W (launched) for different reflectivities of the output coupler (R1) and re-launch efficiencies (${\eta }_1$ corresponds to out-coupling end and ${\eta }_2$ corresponds to high reflectivity end ).

Figure 9. Simulation of output power vs. DCRF length at pump power of 65 W (launched) for different reflectivities of the output coupler (R1) and re-launch efficiencies (${\eta }_1$ corresponds to out-coupling end and ${\eta }_2$ corresponds to high reflectivity end ).

Although it is certainly possible to improve the re-launch efficiency relative to our experimental/fitted values, Figure 9 suggests that already a re-launch loss of 1.25 dB ($\eta =0.75$) in a single end is enough to reduce the conversion efficiency to 21% with 40% out-coupling. However, this out-coupling is not optimized. Figure 10 is similar to Figure 8 and Figure 9, but the out-coupling is optimized for each fiber length. The highest conversion efficiency becomes 62%, in the absence of re-launch loss for short fibers, for which the pump propagation losses become negligible. Realistic re-launch losses of 80% still allow for a conversion efficiency of 40%, at optimum fiber length. Thus, with length optimization and modest improvement in the re-launch efficiency, we can considerably increase the experimentally obtained conversion efficiency, even without any improvements of fiber or pump.

Figure 10. (a) Simulations of conversion efficiency vs. DCRF length with optimized output couplings for different re-launch efficiencies (${\eta }_1$ and ${\eta }_2$); (b) optimum reflectivity of the out-coupling end R1 for different re-launch efficiency corresponding to Figure 10a. In the HR end, $R_2$ = 1 in all cases.

Figure 10. (a) Simulations of conversion efficiency vs. DCRF length with optimized output couplings for different re-launch efficiencies (${\eta }_1$ and ${\eta }_2$); (b) optimum reflectivity of the out-coupling end R1 for different re-launch efficiency corresponding to Figure 10a. In the HR end, $R_2$ = 1 in all cases.

It is also interesting to investigate the effect of improvements in the pump power and fiber loss. For this, we introduce dimensionless variables as follows:

$$\begin{array}{c}\hfill p=\frac{g_R{I}_p}{{\alpha }_s}\\ \hfill s=\frac{\frac{I_s}{h{\nu }_s}}{\frac{I_{p0}}{h{\nu }_p}}=\frac{I_s{\lambda }_s}{I_{p0}{\lambda }_p}\\ \hfill \zeta ={\alpha }_{s}z\end{array}$$

(2)

The normalized pump intensity p is given by the Raman gain it induces, relative to the signal propagation loss. The normalized Stokes intensity s is the Stokes photon flux density relative to the launched pump photon flux density. The normalized propagation coordinate ζ is the physical propagation coordinate relative to the Stokes absorption length. With these substitutions, the Raman propagation equations (Equation (1)) can be rewritten as

$$\begin{array}{c}\hfill \frac{dp}{d\zeta }=-(p_{0}s+\frac{{\alpha }_p}{{\alpha }_s})p\\ \hfill \frac{ds}{d\zeta }=(p-1)s\end{array}$$

(3)

Here, $p_0=g_R{I}_{p0}/{\alpha }_s$ is the normalized launched pump intensity, which is a free parameter that can be viewed as a figure of merit (FoM). For our DCRF with 65 W of pump power, $p_0$ = 4.7. The loss ratio ${\alpha }_p/{\alpha }_s$ is the only other free parameter in the equations. This can often be approximated to unity. Equation (3) is for co-propagating pump and Stokes waves, but it is straightforward to add additional waves, at same or different wavelengths and propagating in the same or opposite direction.

A solution to the normalized Raman propagation equations will be valid for any combination of pump and Stokes intensities (as well as powers) and losses that result in the same normalized parameters, if the boundary conditions and normalized fiber length are the same. This includes solutions that are optimized in terms of output coupling and normalized fiber length. The resulting quantum conversion efficiency is equal to the value of s, as out-coupled from the cavity. Figure 11 shows how the maximum quantum conversion efficiency depends on the FoM, i.e., the normalized launched pump intensity $p_0$, for different re-launch losses. We consider two loss ratios, ${\alpha }_p/{\alpha }_s$ = 1.73 / 1.59 = 1.09 (as for our DCRF) and ${\alpha }_p/{\alpha }_s$ = 1. This difference in loss ratio is small, as is the resulting difference in efficiency (compare the two uppermost curves in Figure 11). With a FoM of 4.7, which corresponds to our experiments with the DCRF fiber, and ${\alpha }_p/{\alpha }_s$ = 1.09, a quantum conversion efficiency of 62% is possible with 100% re-launch efficiency at both ends, and 38% with 50% re-launch efficiency at the out-coupling end and 100% re-launch at the high reflectivity end. In case of the GRIN fiber experiments, the FoM becomes 9.5 if we use an effective area of 1530 μm${}^2$. With this FoM, it is possible to reach 78% conversion efficiency with 100% re-launch efficiency at both ends, and 58% with 50% re-launch efficiency at the out-coupling end and 100% re-launch at high reflectivity end. (This assumes ${\alpha }_p/{\alpha }_s$ = 1.09 whereas actual value is 1.13.) Higher FoMs allow for conversion efficiencies of around 90% for high far-end re-launch efficiencies, although this requires parameters considerably better than those we could reach.

Figure 11. Simulated curves of quantum conversion efficiency vs. figure of merit ($p_0=g_R{I}_{p0}/{\alpha }_s$) for optimized out-coupling and fiber length for different re-launch efficiencies at out-coupling end (${\eta }_1$) and HR re-launch end (${\eta }_2$). Loss ratio ${\alpha }_p/{\alpha }_s$ = 1.09, except for the uppermost curve, which has a loss ratio of 1.

Figure 11. Simulated curves of quantum conversion efficiency vs. figure of merit ($p_0=g_R{I}_{p0}/{\alpha }_s$) for optimized out-coupling and fiber length for different re-launch efficiencies at out-coupling end (${\eta }_1$) and HR re-launch end (${\eta }_2$). Loss ratio ${\alpha }_p/{\alpha }_s$ = 1.09, except for the uppermost curve, which has a loss ratio of 1.

5. Conclusions

In conclusion, we have demonstrated the first-ever FRL cladding-pumped directly by MM diodes. With a GRIN fiber, we demonstrated a record slope efficiency of 80%, which to our knowledge is the highest slope efficiency of any FRL pumped by a highly multimode laser. With cladding-pumping of a DCRF, we observed nearly 10 times the brightness enhancement. We discussed the potential for improving the conversion efficiency with the present scheme by optimizing the out-coupling and fiber length for different re-launch efficiencies. Realistic improvements in pump brightness, fiber NA, fiber loss, and/or coupling losses allow for conversion efficiencies of over 70%.