Design and Implementation of an Optimal Energy Control System for Fixed-Wing Unmanned Aerial Vehicles
Abstract
:1. Introduction
2. Aircraft Energy Equations and Dynamic Model
2.1. Aircraft Energy Equations
2.2. Energy Distribution State-Space Model
2.3. Total Energy Model
3. Aircraft System Identification
3.1. Input Design
3.2. Prediction Error Method (PEM)
3.3. Aircraft Model Evaluation Method
3.4. Total Energy Model
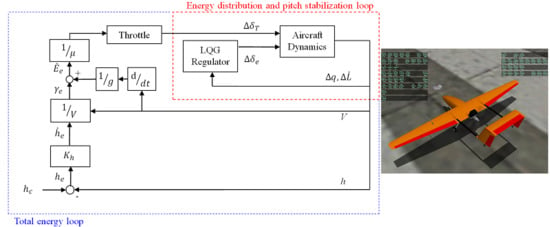
4. Optimal Energy Control System
4.1. OECS Design
4.2. LQG Regulator
5. Simulation Results and Discussion
5.1. Hardware-in-the-Loop System of Spoonbill UAV
5.2. Airspeed and Altitude Hold
5.3. Climbing Maneuver
5.4. Descent Maneuver
5.5. Result Comparison of OECS with Fuzzy Logic Control
5.6. Summary of OECS Performance
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Chen, S.-W.; Chen, P.-C.; Yang, C.-D.; Jeng, Y.-F. Total energy control system for helicopter flight/propulsion integrated controller design. J. Guid. Control Dyn. 2007, 30, 1030–1039. [Google Scholar] [CrossRef]
- Denker, J.S. See How It Flies. Available online: http://www.av8n.com/how/ (accessed on 18 November 2016).
- Lambregts, A. Integrated system design for flight and propulsion control using total energy principles. In Proceedings of the American Institute of Aeronautics and Astronautics, Aircraft Design, Systems and Technology Meeting, Fort Worth, TX, USA, 17–19 October 1983.
- Lambregts, A.A. Vertical flight path and speed control autopilot design using total energy principles. AIAA Pap. 1983. [Google Scholar] [CrossRef]
- Akmeliawati, R.; Mareels, I.M.Y. Nonlinear energy-based control method for aircraft automatic landing systems. IEEE Trans. Control Syst. Technol. 2010, 18, 871–884. [Google Scholar] [CrossRef]
- Kaminer, I.; O’Shaughnessy, P. Integration of four-dimensional guidance with total energy control system. J. Guid. Control Dyn. 1991, 14, 564–573. [Google Scholar] [CrossRef]
- Wu, S.-F.; Guo, S.-F. Optimum flight trajectory guidance based on total energy control of aircraft. J. Guid. Control Dyn. 1994, 17, 291–296. [Google Scholar] [CrossRef]
- Warren, A. Application of total energy control for high-performance aircraft vertical transitions. J. Guid. Control Dyn. 1991, 14, 447–452. [Google Scholar] [CrossRef]
- Voth, C.; Ly, U.-L. Design of a total energy control autopilot using constrained parameter optimization. J. Guid. Control Dyn. 1991, 14, 927–935. [Google Scholar] [CrossRef]
- Bruce, K.; Kelly, J.R.; Person, J.R.L. NASA B737 flight test results of the total energy control system. In Proceedings of the Astrodynamics Conference, Williamsburg, VA, USA, 18–20 August 1986; American Institute of Aeronautics and Astronautics: Reston, VA, USA, 1986. [Google Scholar]
- Rzucidlo, P. TECS/THCS based flight control system for general aviation. In Proceedings of the AIAA Modeling and Simulation Technologies Conference, Chicage, IL, USA, 10–13 August 2009.
- Lamp, M.; Luckner, R. The total energy control concept for a motor glider. In Advances in Aerospace Guidance, Navigation and Control; Springer: Heidelberg, Germany, 2013; pp. 483–502. [Google Scholar]
- Kale, A.; Singhz, G.; Patel, V. 1-adaptive-output feedback based energy control. In Proceedings of the 2015 European Control Conference (ECC), Linz, Austria, 15–17 July 2015; IEEE: New York, NY, USA, 2015; pp. 2792–2797. [Google Scholar]
- Brigido-González, J.; Rodríguez-Cortés, H. Experimental validation of an adaptive total energy control system strategy for the longitudinal dynamics of a fixed-wing aircraft. J. Aerosp. Eng. 2015, 29, 04015024. [Google Scholar] [CrossRef]
- Weiss, S.; Siegwart, R. Real-time metric state estimation for modular vision-inertial systems. In Proceedings of the 2011 IEEE International Conference on Robotics and Automation (ICRA), Shanghai, China, 9–13 May 2011; IEEE: New York, NY, USA; pp. 4531–4537.
- Deittert, M.; Richards, A.; Toomer, C.; Pipe, A. Dynamic soaring flight in turbulence. In Proceedings of the AIAA Guidance, Navigation and Control Conference, Chicago, IL, USA, 10–13 August 2009; pp. 2–5.
- Akhtar, N.; Whidborne, J.F.; Cooke, A.K. Real-Time Trajectory Generation Technique for Dynamic Soaring UAVs; Department of Aerospace Sciences, Cranfield University: Oxfordshire, UK, 2008. [Google Scholar]
- Lee, C.; Chan, W.; Jan, S.; Hsiao, F. A linear-quadratic-gaussian approach for automatic flight control of fixed-wing unmanned air vehicles. Aeronaut. J. 2011, 115, 29–41. [Google Scholar] [CrossRef]
- Lee, C.-S.; Hsiao, F.-B.; Jan, S.-S. Design and implementation of linear-quadratic-gaussian stability augmentation autopilot for unmanned air vehicle. Aeronaut. J. 2009, 113, 275–290. [Google Scholar] [CrossRef]
- Rugh, W.J.; Shamma, J.S. Research on gain scheduling. Automatica 2000, 36, 1401–1425. [Google Scholar] [CrossRef]
- Hsiao, F.-B.; Hsieh, S.-Y.; Chan, W.-L.; Lai, Y.-C. Engine speed and velocity controller development for small unmanned aerial vehicle. J. Aircr. 2008, 45, 725–728. [Google Scholar] [CrossRef]
- Jategaonkar, R. Flight Vehicle System Identification: A Time Domain Methodology; AIAA: Reston, VA, USA, 2006; Volume 216. [Google Scholar]
- Klein, V.; Morelli, E.A. Aircraft System Identification: Theory and Practice; American Institute of Aeronautics and Astronautics: Reston, VA, USA, 2006. [Google Scholar]
- Ljung, L. Prediction error estimation methods. Circuits Syst. Signal Process. 2002, 21, 11–21. [Google Scholar] [CrossRef]
- Lai, Y.C.; Hsiao, F.B. Application of fuzzy logic controller and pseudo-attitude to the autonomous flight of an unmanned aerial vehicle. J. Chin. Inst. Eng. 2010, 33, 387–396. [Google Scholar] [CrossRef]





















| Model | V (m/s) | h (m) | VAF (%) | NRM | ||
|---|---|---|---|---|---|---|
| ∆q | ∆ | ∆q | ∆ | |||
| ft09run06 | 27.03 | 151.0 | 66.99 | 85.37 | 6.09 | 8.58 |
| ft09run07 | 26.50 | 153.4 | 67.12 | 93.57 | 7.22 | 7.48 |
| ft10run01 | 29.33 | 150.5 | 78.12 | 91.99 | 9.27 | 9.84 |
| ft10run02 | 28.43 | 150.7 | 75.54 | 92.44 | 7.99 | 7.21 |
| ft10run07 | 27.44 | 150.8 | - | - | - | - |
| ft10run14 | 28.35 | 151.5 | 57.98 | 86.56 | 3.85 | 4.77 |
| ft10run15 | 29.10 | 150.6 | 54.52 | 91.90 | 5.36 | 5.85 |
| ft10run17 | 28.73 | 150.2 | 65.05 | 94.13 | 5.33 | 5.61 |
| ft10run21 | 28.80 | 151.0 | 89.56 | 94.82 | 5.37 | 6.48 |
| ft11run07 | 27.98 | 150.7 | 58.92 | 87.65 | 5.90 | 3.88 |
| ft11run10 | 27.65 | 150.8 | 71.75 | 84.84 | 8.63 | 7.51 |
| ft11run25 | 28.40 | 151.0 | 76.16 | 91.03 | 2.97 | 6.07 |
| ft11run28 | 29.25 | 156.7 | 89.49 | 90.87 | 4.68 | 4.05 |
| Flight Tests | V (m/s) | h (m) | |
|---|---|---|---|
| ft33run10 | 30.0 | 150.5 | 0.0050 |
| ft33run11 | 30.2 | 152.6 | 0.0045 |
| ft33run12 | 30.0 | 150.7 | 0.0050 |
| ft33run13 | 30.0 | 151.0 | 0.0050 |
| ft33run14 | 30.1 | 153.0 | 0.0050 |
| Average | - | - | 0.0049 |
| No. | ||
|---|---|---|
| 1 | 0.130 | |
| 2 | 0.045 | |
| 3 | 0.025 | |
| 4 | 0.008 |
| Condition | Windless | Wind | ||||
|---|---|---|---|---|---|---|
| Maneuver | Level | Climb | Descend | Level | Climb | Descend |
| Altitude Tracking (m) | 150 | 150→158 | 158→150 | 150 | 120→150 | 150→120 |
| Settling Time (s) | - | 40 | 40 | - | 65 | 65 |
| ∆q (rad/s) | 0.01 | 0.01 | 0.01 | 0.15 | 0.15 | 0.15 |
| 0.01 | 0.01 | 0.01 | 0.05 | 0.10 | 0.10 | |
| Altitude Deviation (m) | 0.20 | 0.20 | 0.20 | 2.00 | 2.00 | 2.00 |
| Airspeed Deviation (m/s) | 0.10 | 0.20 | 0.20 | 0.50 | 1.00 | 1.00 |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lai, Y.-C.; Ting, W.O. Design and Implementation of an Optimal Energy Control System for Fixed-Wing Unmanned Aerial Vehicles. Appl. Sci. 2016, 6, 369. https://doi.org/10.3390/app6110369
Lai Y-C, Ting WO. Design and Implementation of an Optimal Energy Control System for Fixed-Wing Unmanned Aerial Vehicles. Applied Sciences. 2016; 6(11):369. https://doi.org/10.3390/app6110369
Chicago/Turabian StyleLai, Ying-Chih, and Wen Ong Ting. 2016. "Design and Implementation of an Optimal Energy Control System for Fixed-Wing Unmanned Aerial Vehicles" Applied Sciences 6, no. 11: 369. https://doi.org/10.3390/app6110369
APA StyleLai, Y. -C., & Ting, W. O. (2016). Design and Implementation of an Optimal Energy Control System for Fixed-Wing Unmanned Aerial Vehicles. Applied Sciences, 6(11), 369. https://doi.org/10.3390/app6110369