The Ultrasonic Polar Scan for Composite Characterization and Damage Assessment: Past, Present and Future †
Abstract
:1. Introduction
2. The Past: 1981–2010
3. The Present: 2010–2015
- lack of high quality experimental data,
- lack of a computationally efficient simulation model, and
- lack of adequate inverse modeling techniques to couple experiment to simulation.
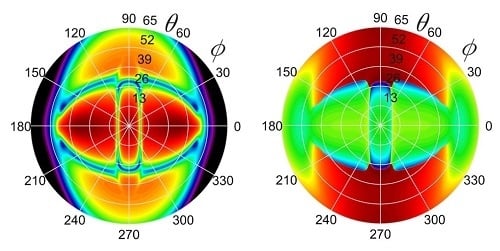
3.1. The Ultrasonic Polar Scan Revisited
3.2. Extensions of UPS Method
3.2.1. Harmonic Ultrasonic Polar Scan
3.2.2. Ultrasonic Backscatter Polar Scan (UBPS)
3.3. Applications of UPS and UBPS
3.3.1. Static Damage
3.3.2. Delamination
3.3.3. Fatigue Damage
3.3.4. (Sub)surface Corrugation
3.3.5. Strain Measurement
4. The (Near) Future: 2015–...
4.1. Viscoelastic Tensor
4.2. Nonlinear U(B)PS
4.3. Redesign of UPS Scanner
4.4. Comprehensive Inspection Approach
5. Conclusions
- ○
- (Visco)elastic C-tensor identification through the use of inverse methods.
- ○
- Assessment of (quasi-)static shear damage in cross-ply C/E laminate.
- ○
- Detection of (overlapping) delamination in thin cross-ply C/E laminate.
- ○
- Assessment of tension-tension fatigue damage in woven C/E laminate.
- ○
- Identification of the in-plane parameters of 2D (sub)surface corrugation.
- ○
- Single-sided identification of a local 3D plastic strain field in DC06 steel coupon.
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Van Dreumel, W.H.M.; Speijer, J.L. Non-destructive composite laminate characterization by means of ultrasonic polar-scan. Mater. Eval. 1981, 39, 922–925. [Google Scholar]
- Declercq, N.F.; Degrieck, J.; Leroy, O. Simulations of harmonic and pulsed ultrasonic polar scans. NDT E Int. 2006, 39, 205–216. [Google Scholar] [CrossRef]
- Rokhlin, S.I.; Chimenti, D.E.; Nagy, P.B. Physical Ultrasonics of Composites; Oxford University Press: Oxford, UK, 2011. [Google Scholar]
- Rose, J.L. Ultrasonic Waves in Solid Media; Cambridge University Press: Oxford, UK, 1999. [Google Scholar]
- Kersemans, M.; Martens, A.; Delrue, S.; van den Abeele, K.; Pyl, L.; Zastavnik, F.; Sol, H.; Degrieck, J.; van Paepegem, W. The ultrasonic polar scan: Past, Present and future. In Proceedings of the Emerging Technologies in NonDestructive Testing (ETNDT6), Brussels, Belgium, 27–29 May 2015; pp. 133–139.
- Van Dreumel, W.H.M.; Speijer, J.L. Polar-scan, a non-destructive test method for the inspection of layer orientation and stacking order in advanced fiber composites. Mater. Eval. 1983, 41, 1060–1062. [Google Scholar]
- Degrieck, J.; van Leeuwen, D. Simulatie van een Ultrasone Polaire Scan van een Orthotrope Plaat (in Dutch). In Proceedings of the 3rd Belgian National Congress on Theoretical and Aplied Mechanics, Liege, Belgium, 30–31 May 1994.
- Degrieck, J. Some possibilities of nondestructive characterisation of composite plates by means of ultrasonic polar scans. In Proceedings of the Emerging technologies in nondestructive testing (ETNDT), Patras, Greece, 22–23 May 1995; pp. 225–235.
- Degrieck, J.; Declercq, N.F.; Leroy, O. Ultrasonic polar scans as a possible means of non-destructive testing and characterisation of composite plates. Insight 2003, 45, 196–201. [Google Scholar] [CrossRef]
- Declercq, N.F.; Degrieck, J.; Leroy, O. On the influence of fatigue on ultrasonic polar scans of fiber reinforced composites. Ultrasonics 2004, 42, 173–177. [Google Scholar] [CrossRef] [PubMed]
- Declercq, N.F.; Degrieck, J.; Leroy, O. Ultrasonic polar scans: Numerical simulation on generally anisotropic media. Ultrasonics 2006, 45, 32–39. [Google Scholar] [CrossRef] [PubMed]
- Satyanarayan, L.; Weide, J.M.V.; Declercq, N.F. Ultrasonic polar scan imaging of damaged fiber reinforced composites. Mater. Eval. 2010, 68, 733–739. [Google Scholar]
- Kersemans, M. Combined experimental-numerical study to the ultrasonic polar scan for inspection and characterization of (damaged) anisotropic materials. Ph.D. Thesis, Ghent University, Ghent, Belgium, 31 October 2014. [Google Scholar]
- Kersemans, M.; van Paepegem, W.; van den Abeele, K.; Pyl, L.; Zastavnik, F.; Sol, H.; Degrieck, J. Pitfalls in the experimental recording of ultrasonic (backscatter) polar scans for material characterization. Ultrasonics 2014, 54, 1509–1521. [Google Scholar] [CrossRef] [PubMed]
- Kersemans, M.; Martens, A.; van den Abeele, K.; Degrieck, J.; Pyl, L.; Zastavnik, F.; Sol, H.; van Paepegem, W. The quasi-harmonic ultrasonic polar scan for material characterization: Experiment and numerical modeling. Ultrasonics 2015, 58, 111–122. [Google Scholar] [CrossRef] [PubMed]
- Rokhlin, S.I.; Wang, L. Stable recursive algorithm for elastic wave propagation in layered anisotropic media: Stiffness matrix method. J. Acoust. Soc. Am. 2002, 112, 822–834. [Google Scholar] [CrossRef] [PubMed]
- Tan, E.L. Hybrid compliance-stiffness matrix method for stable analysis of elastic wave propagation in multilayered anisotropic media. J. Acoust. Soc. Am. 2006, 119, 45–53. [Google Scholar] [CrossRef] [PubMed]
- Tan, E.L. Stiffness matrix method with improved efficiency for elastic wave propagation in layered anisotropic media. J. Acoust. Soc. Am. 2005, 118, 3400–3403. [Google Scholar] [CrossRef]
- Kersemans, M.; Martens, A.; Lammens, N.; van den Abeele, K.; Degrieck, J.; Zastavnik, F.; Pyl, L.; Sol, H.; van Paepegem, W. Identification of the elastic properties of isotropic and orthotropic thin-plate materials with the pulsed ultrasonic polar scan. Exp. Mech. 2014, 54, 1121–1132. [Google Scholar] [CrossRef] [Green Version]
- Kersemans, M.; Lammens, N.; Luyckx, G.; Degrieck, J.; van Paepegem, W. Quantitative measurement of the elastic properties of orthotropic composites by means of the ultrasonic polar scan method. JEC Compos. 2012, 75, 48–52. [Google Scholar]
- Martens, A.; Kersemans, M.; Degrieck, J.; van Paepegem, W.; Delrue, S.; van den Abeele, K. Time-of-flight recorded pulsed ultrasonic polar scan for elasticity characterization of composites. In Proceedings of the Emerging Technologies in NonDestructive Testing (ETNDT6), Brussels, Belgium, 27–29 May 2015.
- Van den Abeele, K.; Martens, A.; Kersemans, M.; Degrieck, J.; Delrue, S.; van Paepegem, W. Characterization of visco-elastic material parameters by means of the ultrasonic polar scan method. In Proceedings of the Acoustical Society of America—Fall 2015 Meeting, Jacksonville, FL, USA, 2–6 November 2015.
- Kersemans, M.; Lammens, N.; Degrieck, J.; van den Abeele, K.; Pyl, L.; Zastavnik, F.; Sol, H.; van Paepegema, W. Extraction of bulk wave characteristics from a pulsed ultrasonic polar scan. Wave Motion 2014, 51, 1071–1081. [Google Scholar] [CrossRef]
- Kersemans, M.; van Paepegem, W.; Lemmens, B.; van den Abeele, K.; Pyl, L.; Zastavnik, F.; Sol, H.; Degrieck, J. The pulsed ultrasonic backscatter polar scan and its applications for NDT and material characterization. Exp. Mech. 2014, 54, 1059–1071. [Google Scholar] [CrossRef]
- Kersemans, M.; van Paepegem, W.; van den Abeele, K.; Pyl, L.; Zastavnik, F.; Sol, H.; Degrieck, J. Ultrasonic characterizaion of subsurface 2D corrugation. J. Nondestruct. Eval. 2014, 33, 438–442. [Google Scholar] [CrossRef] [Green Version]
- De Billy, M.; Cohentenoudji, F.; Jungman, A.; Quentin, G.J. Possibility of assigning a signature to rough surfaces using ultrasonic backscattering diagrams. IEEE Trans. Sonics Ultrason. 1976, 23, 356–363. [Google Scholar] [CrossRef]
- De Billy, M.; Quentin, G. Measurement of the periodicity of internal surfaces by ultrasonic testing. J. Phys. D Appl. Phys. 1982, 15, 1835–1841. [Google Scholar] [CrossRef]
- Herbison, S.W. Ultrasonic diffraction effects on periodic surfaces. Ph.D. Thesis, Georgia Institute of Technology, Atlanta, GA, USA, August 2011. [Google Scholar]
- Kersemans, M.; de Baere, I.; Degrieck, J.; van den Abeele, K.; Pyl, L.; Zastavnik, F.; Sol, H.; van Paepegem, W. Nondestructive damage assessment in fiber reinforced composites with the pulsed ultrasonic polar scan. Polym. Test. 2014, 34, 85–96. [Google Scholar] [CrossRef]
- Kersemans, M.; Martens, A.; van den Abeele, K.; Degrieck, J.; Pyl, L.; Zastavnik, F.; Sol, H.; van Paepegem, W. Detection and localization of delaminations in thin carbon fiber reinforced composites with the ultrasonic polar scan. J. Nondestruct. Eval. 2014, 33, 522–534. [Google Scholar] [CrossRef]
- Giancane, S.; Panella, F.W.; Dattoma, V. Characterization of fatigue damage in long fiber epoxy composite laminates. Int. J. Fatigue 2010, 32, 46–53. [Google Scholar] [CrossRef]
- Taheri-Behrooz, F.; Shokrieh, M.M.; Lessard, L.B. Residual stiffness in cross-ply laminates subjected to cyclic loading. Compos. Struct. 2008, 85, 205–212. [Google Scholar] [CrossRef]
- Kersemans, M.; de Baere, I.; Degrieck, J.; van den Abeele, K.; Pyl, L.; Zastavnik, F.; Sol, H.; van Paepegem, W. Damage signature of fatigued fabric reinforced plastic in the pulsed ultrasonic polar scan. Exp. Mech. 2014, 54, 1467–1477. [Google Scholar] [CrossRef] [Green Version]
- Lyman, T. An explanation of the false spectra from diffraction gratings. Proc. Am. Acad. Arts Sci. 1903, 39, 39–47. [Google Scholar] [CrossRef]
- Gale, H.G. Rowland ghosts. Astrophys. J. 1937, 85, 49–61. [Google Scholar] [CrossRef]
- Kersemans, M.; Allaer, K.; van Paepegem, W.; van den Abeele, K.; Pyl, L.; Zastavnik, F.; Sol, H.; Degrieck, J. A novel ultrasonic strain gauge for single-sided measurement of a local 3D strain field. Exp. Mech. 2014, 54, 1673–1685. [Google Scholar] [CrossRef] [Green Version]
- Castaings, M.; Hosten, B.; Kundu, T. Inversion of ultrasonic, plane-wave transmission data in composite plates to infer viscoelastic material properties. NDT E Int. 2000, 33, 377–392. [Google Scholar] [CrossRef]
- Wang, L.; Lavrentyev, A.I.; Rokhlin, S.I. Beam and phase effects in angle-beam-through-transmission method of ultrasonic velocity measurement. J. Acoust. Soc. Am. 2003, 113, 1551–1559. [Google Scholar] [CrossRef] [PubMed]
- Lavrentyev, A.I.; Rokhlin, S.I. Determination of elastic moduli, density, attenuation, and thickness of a layer using ultrasonic spectroscopy at two angles. J. Acoust. Soc. Am. 1997, 102, 3467–3477. [Google Scholar] [CrossRef]
- Cawley, P.; Hosten, B. The use of large ultrasonic transducers to improve transmission coefficient measurements on viscoelastic anisotropic plates. J. Acoust. Soc. Am. 1997, 101, 1373–1379. [Google Scholar] [CrossRef]
- Castellano, A.; Foti, P.; Fraddosio, A.; Marzano, S.; Piccioni, M.D. Mechanical characterization of CFRP composites by ultrasonic immersion tests: Experimental and numerical approaches. Compos. B Eng. 2014, 66, 299–310. [Google Scholar] [CrossRef]
- Aymerich, F.; Staszewski, W.J. Impact damage detection in composite laminates using nonlinear acoustics. Compos. A Appl. Sci. Manuf. 2010, 41, 1084–1092. [Google Scholar] [CrossRef]
- Scalerandi, M.; Gliozzi, A.S.; Bruno, C.L.E.; van den Abeele, K. Nonlinear acoustic time reversal imaging using the scaling subtraction method. J. Phys. D Appl. Phys. 2008, 41, 1–10. [Google Scholar] [CrossRef]
- Meo, M.; Polimeno, U.; Zumpano, G. Detecting damage in composite material using nonlinear elastic wave spectroscopy methods. Appl. Compos. Mater. 2008, 15, 115–126. [Google Scholar] [CrossRef]
- Hirsekorn, S.; Rabe, U.; Arnold, W. Characterisation and evaluation of composite materials by nonlinear ultrasonic transmission measurements. In Proceedings of the International Congress on Ultrasonics (ICU 2007), Wenen, Oostenrijk, 10–12 April 2007.
- Drinkwater, B.W.; Wilcox, P.D. Ultrasonic arrays for non-destructive evaluation: A review. NDT E Int. 2006, 39, 525–541. [Google Scholar] [CrossRef]
- Rucka, M. Damage detection in beams using wavelet transform on higher vibration modes. J. Theor. Appl. Mech. 2011, 49, 399–417. [Google Scholar]
- Baba, B.O.; Thoppul, S.; Gibson, R.F. Experimental and numerical investigation of free vibrations of composite sandwich beams with curvature and debonds. Exp. Mech. 2010, 51, 857–868. [Google Scholar] [CrossRef]
- Pitarresi, G. Lock-in signal post-processing techniques in infra-red thermography for materials structural evaluation. Exp. Mech. 2013, 55, 667–680. [Google Scholar] [CrossRef]
- Wong, A.K.; Rajic, N.; Nguyen, Q. 50th anniversary article: Seeing stresses through the thermoelastic lens—A retrospective and prospective from an australian viewpoint. Strain 2015, 51, 1–15. [Google Scholar] [CrossRef]
- Hung, Y.Y.; Chen, Y.S.; Ng, S.P.; Liu, L.; Huang, Y.H.; Luk, B.L.; Ip, R.W.L.; Wu, C.M.L.; Chung, P.S. Review and comparison of shearography and active thermography for nondestructive evaluation. Mater. Sci. Eng. R Rep. 2009, 64, 73–112. [Google Scholar] [CrossRef]
- Klepka, A.; Pieczonka, L.; Staszewski, W.J.; Aymerich, F. Impact damage detection in laminated composites by non-linear vibro-acoustic wave modulations. Compos. B Eng. 2014, 65, 99–108. [Google Scholar] [CrossRef]
















| Corrugation Parameters | Design Values | Ultrasonic Reconstruction | Optical Measurement |
|---|---|---|---|
| Λ1 | 250 μm | 249.8 μm | 250.1 μm |
| Φ1 | 100° | 99.3° | 99.2° |
| Λ2 | 375 μm | 375.3 μm | 374.8 μm |
| Φ2 | 10° | 9° | 9.1° |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons by Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kersemans, M.; Martens, A.; Degrieck, J.; Van Den Abeele, K.; Delrue, S.; Pyl, L.; Zastavnik, F.; Sol, H.; Van Paepegem, W. The Ultrasonic Polar Scan for Composite Characterization and Damage Assessment: Past, Present and Future. Appl. Sci. 2016, 6, 58. https://doi.org/10.3390/app6020058
Kersemans M, Martens A, Degrieck J, Van Den Abeele K, Delrue S, Pyl L, Zastavnik F, Sol H, Van Paepegem W. The Ultrasonic Polar Scan for Composite Characterization and Damage Assessment: Past, Present and Future. Applied Sciences. 2016; 6(2):58. https://doi.org/10.3390/app6020058
Chicago/Turabian StyleKersemans, Mathias, Arvid Martens, Joris Degrieck, Koen Van Den Abeele, Steven Delrue, Lincy Pyl, Filip Zastavnik, Hugo Sol, and Wim Van Paepegem. 2016. "The Ultrasonic Polar Scan for Composite Characterization and Damage Assessment: Past, Present and Future" Applied Sciences 6, no. 2: 58. https://doi.org/10.3390/app6020058
APA StyleKersemans, M., Martens, A., Degrieck, J., Van Den Abeele, K., Delrue, S., Pyl, L., Zastavnik, F., Sol, H., & Van Paepegem, W. (2016). The Ultrasonic Polar Scan for Composite Characterization and Damage Assessment: Past, Present and Future. Applied Sciences, 6(2), 58. https://doi.org/10.3390/app6020058