1. Introduction
Sound synthesis techniques for string instruments have evolved, in the past few decades, from abstract synthesis [
1] (wavetables, frequency-modulation (FM) synthesis ...) towards sampling synthesis, based on a library of pre-recorded sounds, and physical models, emulating the instruments themselves. To this day, the best synthesised sound quality is achieved by sampling techniques; however, the potentially very large storage requirements for these sound libraries are a major argument for using physical models. Beyond the storage concerns, the use of a physical model allows for great flexibility for input parameters (typically, the instrument’s shape and material properties, together with the player’s controls), as well as output parameters, usually the “listening conditions”, that can be changed freely and dynamically along a simulation, as opposed to the case of statically recorded samples.
Physical modelling synthesis for strings debuted in the 1970s, with time stepping methods to discretise and directly solve the 1D wave equation [
2,
3,
4]. However, the very limited computational power at the time ruled out simulation at an audio sample rate in any reasonable amount of time. The next generation of models therefore focussed on algorithmic simplification, through physically plausible assumptions. The physics-based Karplus-Strong string synthesis algorithm [
5,
6] was generalised by the digital waveguide framework [
7,
8]; Karjalainen
et al. [
9] review the use of these models for string synthesis. Their fast execution and realistic sound output found efficient applications in bowed string modelling, and are still widely used to this day [
10,
11,
12,
13,
14]. Digital waveguides model the forward and backward travelling waves along a string using delay lines—a simple and efficient strategy for certain linear time invariant systems. In particular, they are well suited for systems in one dimension, well described by the wave equation. Another more general class of physical models relies on the modal solutions of the string equation, and has been successfully adapted for bowed strings [
15,
16].
However, the very assumptions that underlie the efficiency of these methods can lead to difficulties when extensions to more realistic settings are desired—the bowed string and its complex, nonlinear, time-varying interaction with the environment being an excellent example. Time-stepping methods, and more specifically finite difference methods [
17], though computationally costly, have regained appeal in musical sound synthesis [
18] with the great increase in computing power during the last two decades. String simulation in one dimension is particularly suited for these kind of methods [
19,
20]. The interactions of, say, a bowed string with its environment can be included in a straightforward manner, as long as they can be described with a system of partial differential equations (PDEs). These methods also allow a greater flexibility for modelling the musician’s gestures, and more generally to deal with the dynamic nature of the input and output parameters.
While the number of parameters is small compared to other methods, navigating the space they describe is somewhat of a challenge. Indeed, as opposed to a struck or plucked string, the continuous excitation mechanism of a bowed string makes playability a major issue, for real or virtual instruments. The player shapes the sound and behaviour of his instrument throughout the whole production of a note. Their gestures can be described with a handful of parameters, which must be perfectly coordinated at all times to allow a tone to be created and sustained; indeed, Schelleng [
21], following the work of Raman [
22] some decades earlier, was the first to analytically show that, under simplifying assumptions and for a certain bow velocity, only a relatively narrow triangular area (in logarithmic scale) in the downwards bow force versus bow-bridge distance parameter space gave rise to the characteristic stable Helmholtz motion desired by most musicians (his work was revised by Schoonderwaldt
et al. [
23], introducing more refined elements of bowed string motion). This area is tied to the concept of playability, and the so-called Schelleng diagrams are widely used in bowed string playability studies [
24,
25,
26,
27]. Transient quality also constitutes a major part of playability: Guettler [
28] investigated the relation between bow downwards force and bow acceleration regarding the quality of initial transients, producing triangular diagrams resembling those of Schelleng, again under simplifying assumptions; Woodhouse
et al. [
29] produced Guettler diagrams with more refined numerical models as well as experimental data, showing the predicted wedge-shaped region. A detailed review of the published literature on bowed string mechanics (and, indeed, violin acoustics in general) was recently written by Woodhouse [
30].
After the studies of Schelleng, an experimental study by Askenfelt [
31,
32] yielded measured values for these control parameters, on a violin; he was the first to develop a measuring rig able to record them all simultaneously during performance. More recently, the variation of these parameters along various bowed string gestures was observed and analysed in detail [
15,
33,
34]. The obtained signals can be mathematically reconstructed [
35], or directly used, to be fed into a physical modelling algorithm such as the one presented in this work. The aforementioned studies are mainly interested in bowing gestures; to handle those of the left hand fingers (vibrato, legato, glissando, etc.), one can include a finger model, along with a fingerboard.
This work is concerned with a detailed model of bowed string vibration, emphasising the interactions of the string with the player. A linear bowed string is simulated in two polarisations. The model includes the following features:
in one polarisation, distributed nonlinear contact interactions between the string and the dynamic left hand fingers, dynamic bow, and fingerboard. A stable finite difference scheme for modelling distributed contact/collisions has recently been established [
36,
37], that can be used in this stopped string-fingerboard setup [
38,
39];
in the other polarisation, orthogonally to the first, distributed nonlinear friction forces between the string and the same three objects. The friction force nonlinearity is modelled with a force/velocity friction curve for the bow [
40]. Tangential Coulomb friction also keeps the string captured between the fingers and fingerboard during note production;
full control over the physical parameters of the system, as well as dynamic variations of the playing parameters. This time domain model is therefore able to reproduce most bowed string gestures;
introduction of an inertial term in the bow model, in the tangential direction. This leads to a horizontal force bow control, instead of the bow velocity input signal used in most of the aforementioned models;
in the same direction, introduction of an inertial term and a restoring term in the finger model. The fingertip is massive, absorbs some of the tangential string vibrations, and oscillates about a fixed horizontal finger position.
The main challenges associated with this model are computational. On one hand, the resulting numerical method must be stable; energy methods are used to derive a stability condition from the model system, and establish a power balance to keep track of the energy exchanges between the various parts of the system. On the other hand, the distributed nonlinearities induce heavy computational costs, with the need to resort to iterative nonlinear system solving methods; extensive optimisation is necessary in order to bring the algorithm closer to real-time operation. Finally, the gestural control is obviously limited by the aforementioned playability issues; such a model is able to produce waveforms outside of the generally desired Helmholtz sawtooth, and the absence of direct feedback for the player in the present algorithm indeed makes parameter control a rather fastidious task.
In
Section 2, the model equations for the bow/string system are presented, with an elaborate description of finger/string interaction in the case of stopped notes, and the string/fingerboard collision interaction. A globally energy balanced finite difference scheme is presented in
Section 3. Finally, bowed string simulation results, with the reproduction of several typical gestures, are presented in
Section 4. Some sound and video examples from the computed simulations are available online [
41].
2. Model Description
2.1. Context
The choice of time-stepping methods is in line with the larger aim of building full physical models of musical instruments, embedded in virtual acoustic spaces. The work presented here is a step towards designing such a model for a bowed string instrument; this longer term aim guided the choice of whether or not to include certain features of bowed string playing in this work.
As a consequence, although the bowed string model described here uses sensible, physical assumptions, some of its features may not be as refined as one can find in some of the recent literature. This is the result of compromising between physical accuracy, computational complexity, and (subjective) synthetic sound quality. Some features, for instance, have been neglected for dramatically increasing the algorithmic complexity and computational load, while having very little influence to both the output sound and the control quality; this is the case for e.g., the nonlinear intrinsic coupling between the two polarisations of the string, or the thermal properties of the rosin layer coating the bow [
42]. Torsion waves are also excluded; although, when present, their synchronisation with transverse waves has been experimentally shown to strongly contribute to tone quality and stability [
43], their presence (or absence) may not have a strong bearing on the playability and synthetic sound quality of a simplified physical model [
25].
2.2. A Linear, Two-Polarisation String Model
A dual-polarisation string model serves two main purposes in this work. First, treated in this paper, is the ability to simulate realistic, nonlinear impact interactions between the string and any external objects in one direction, translating directly into tangential friction forces in the other direction. This is an intuitive way to include not only a bow that is able to naturally bounce, but also dynamic left hand fingers to stop the string against a fingerboard, while absorbing some of the string vibrations.
Second is the potential to use this algorithm towards a model of a full instrument. The coupling of the two polarisations at the bridge boundary, through a model of the bridge itself coupled to the instrument body, would be straightforwardly achieved with this string model as a starting point. While the incorporation of the bridge and wooden cavity is undoubtedly crucial to the final sound of the virtual instrument, let us first describe the proposed string model.
2.3. The Isolated String
Consider a linear, stiff, and lossy string, of length
L. The string displacement in the
vertical or
normal polarisation is denoted by
, while
is the string displacement in the
horizontal or
tangential polarisation. Both are defined for position
and time
(see
Figure 1).
The partial differential equations governing the time evolution of
and
can be written as:
is the partial differential operator defined as [
20]:
where
is equivalent to
.
is the linear mass density of the string, in kg/m;
T is the tension of the string, in N;
is the bending stiffness, where
E is Young’s modulus in Pa, and
is the area moment of inertia of the circular cross-section of the string, with
r the string radius in m. Some typical parameters for a violin, a viola, and a cello, can be found in the literature, notably those measured by Pickering [
44] and Percival [
45].
(1/s) and
(m
2/s) are positive damping coefficients, that empirically account for frequency independent and dependent losses in the string, respectively. With more refinement, they could be replaced by a full model accounting for energy dissipation through air viscosity, acoustic radiation, and internal friction, each of these three mechanisms having a more or less pronounced impact across the spectrum [
46]. In accordance with the statements in
Section 2.1 however, this empirical, simplified loss model is deemed sufficient for the purposes of this work.
The system described by Equations (1) and (2) is accompanied by a set of boundary conditions (four of them for each polarisation of the stiff string). Standard energy conserving conditions of the simply supported type are chosen, assuming an isolated string, with no interaction with the instrument body (note that for the musical string, the effect of bending stiffness being very small with respect to that of tension, there is little difference between the simply supported and clamped boundary conditions):
It is worth noting that although definitely worth investigating, intrinsic and/or boundary coupling between the two polarisations is not included in the present model, although, as mentioned in
Section 2.2, boundary coupling could be introduced through modelling the bridge and body. As will be clarified in
Section 2.4 and
Section 2.5, physical coupling between the two directions of vibration occurs where the string is in contact with the bow, finger, or fingerboard.
2.4. Vertical Polarisation
2.4.1. The Collision Interaction
The collision model used in this paper was formalised in 1975 by Hunt and Crossley [
47], as a means to write a new law governing the mechanics of nonlinear damped impacts. The undamped power-law model was adopted by the musical acoustics community as a means to describe lumped collisions, especially hammer-string collisions in the piano [
19,
48,
49], and mallet-membrane impacts in drums [
50,
51]. A similar model than that of Hunt and Crossley, with hysteretic damping, was used for the modelling of the interaction between the piano hammer felt and the piano string, with good concordance with experimental results, by Stulov [
52]. A numerical time domain framework for this particular model has been developed throughout the recent few years [
36,
37], and has proven to give rise to stable schemes; this aspect will be further developed in
Section 3.3.
This type of contact interaction is chosen for two modelling aspects of bowed string playing. First and foremost, a bow having the ability to naturally bounce is a necessary feature for a wide range of the musician’s gestural palette, such as
spiccato or
ricochet bowing. Introducing a collision mechanism in the bow model itself allows for this bouncing under realistic playing parameters. The natural frequency of the bouncing bow varies between 6 and 30 Hz, depending on whether the string is bowed closer to the tip or the frog of the bow [
53]; this can be tuned by changing the stiffness and mass parameters of the bow model. It is worth noting that the entire dynamics of the bow hair have purposely been excluded from this work; as the primary aim is sound synthesis, it is found here that a dynamic, nonlinear, albeit lumped bow is a satisfying compromise between computational cost and gestural versatility.
The second aspect of the contact interaction lies in the capture of the string between a left hand finger and the fingerboard. The use of the damped impact law allows for realistic simulation of the fingertip reacting against the tension of the string, while significantly absorbing vibrations. The distributed fingerboard acts as a continuous barrier for fingers to slide along, allowing for
glissando and
vibrato gestures on the fly. Again, the built-in impact model allows for string rattling effects [
39], used, for instance, in jazz double bass playing.
2.4.2. Bow and Finger
At a physical level, in the vertical polarisation, the bow and finger are essentially modelled the same way—that is, a lumped, flexible body pushing down on the string. The distinction lies in the values of the various parameters which define the collision force. For instance, the bow hair may have different stiffness properties than that of the fingertip, and the latter definitely exhibits higher damping than the former.
Adding the finger and bow forces to the string model described in Equation (1a) gives:
where the downward forces exerted by the finger and the bow onto the string are respectively denoted by
and
. Their action on the string is localised as defined by the continuous distributions
and
, possibly time-varying (one can use, e.g., a Dirac delta function to model a pointwise interaction).
and
can be written using the Hunt and Crossley collision model mentioned in
Section 2.4.1:
where the dot notation is used for total time differentiation (
).
These contact forces are nonlinear functions of the penetration
and
, corresponding to the distance by which the colliding object (here, the fingertip and the bow hair, respectively) would deform from its resting shape.
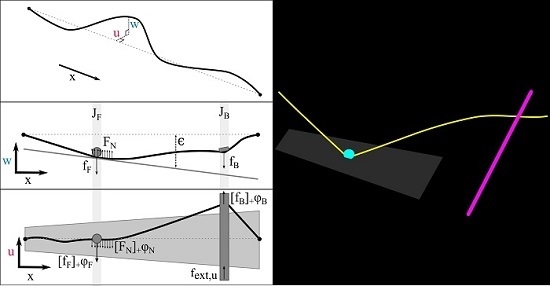
Figure 2a,b provide a visual interpretation of the finger and the bow penetrations.
and
are defined as:
where
and
are respectively the vertical positions of the finger and bow at time
t (see
Figure 2).
and
are nonlinear potential functions, related to the stored collision energy.
and
are nonlinear damping coefficients. They can be written as:
where
means
.
The parameters and , both strictly positive, define the respective stiffnesses of the finger and the bow. and are power law exponents, both larger than 1. and are positive damping factors.
and
are respectively the vertical positions of the finger and bow at time
t (see
Figure 2). Their behaviour is governed by:
where
,
are the finger and bow masses, respectively (in kg), and
,
are the external forces applied vertically on the finger and bow, respectively (in N).
2.4.3. Fingerboard
The fingerboard forms a distributed barrier under the string. Equation (4) therefore generalises to:
where the index
indicates “neck”, to avoid confusion.
is the contact force density exerted by the neck onto the string, along its length (in N/m). Here, the Hunt and Crossley collision model is used again, this time as a smooth approximation to a rigid collision:
Once again, the contact force is a function of the fingerboard penetration
, defined over
:
where
is the position of the fingerboard with respect to the string at rest (
i.e., the action of the instrument).
Figure 3 summarises the forces at play in the vertical polarisation.
and
are defined analogously to the finger and bow functions in Equations (8) and (9):
where
is chosen very large to approach an ideally rigid collision. Indeed, such a choice ensures that
stays very small, as should be for fingerboard-like structures [
39].
2.5. Horizontal Polarisation
2.5.1. The Friction Interaction
The vertical contact forces described in
Section 2.4 give rise to corresponding tangential friction forces onto the string, in the horizontal polarisation. A classic dry friction model is used, where the friction force is directly proportional to the normal force:
where
is the tangential friction force (in N),
is a dimensionless friction coefficient, and
is the normal contact force, applied downwards on the string. The neck, finger and bow are not considered adhesive, therefore friction exists only for positive normal forces.
The friction force therefore arises from a friction coefficient, modulated by the normal force applied on the string. As a result, the interactions in the vertical polarisation feed into the horizontal polarisation. It is important to note that, for this particular framework, this is the coupling point between the two modelled directions; as mentioned earlier in
Section 2.3, there is no other form of polarisation coupling in this model.
The friction coefficient can be defined as dependent on the relative velocity between the string and the external object. One can therefore establish a force-velocity friction curve, mapping the friction coefficient to a particular value of the relative velocity .
2.5.2. Bow
The most straightforward way to introduce the tangential friction forces is probably to come back to the simple bowed string, where the friction phenomenon is the most appreciable. The bowed string equation in the horizontal polarisation is:
where
and
are the distribution and the normal collision force defined in
Section 2.4.2. Note the negative sign in front of the friction term, reflecting the friction force opposing the motion of the string.
is a dimensionless friction coefficient, depending on
, the relative velocity between the bow hair and the string. These are defined as [
42]:
where
is the bow transverse displacement. As the bow is pushed across the string, the equation governing the transverse motion of the bow is:
is a positive coefficient quantifying the linear energy absorption by the bow in the horizontal direction. The linear damping term is negligible compared to the friction term, when the string is in contact with the bow; indeed, this linear term mainly has a practical purpose in the numerical simulations, that is to avoid the bow drifting away when it is lifted from the string at the end of a note.
is the force with which the player pushes the bow tangentially, in order to establish the desired bow velocity. Note the slight difference with the usual control parameter in most bowed string studies; instead of directly imposing a bow velocity , the force applied by the player on the bow is used, resulting in a bow velocity .
The choice of a friction coefficient depending on relative velocity,
, while already quite refined and fairly costly to model, is nonetheless somewhat of a trade-off between computational simplification and physical realism. More elaborate models for the bowed string friction interaction, involving viscothermal effects in the rosin layer coating the bow hair, can be used [
13,
14]; however, they require significantly more advanced implementations. Satisfying results and synthetic sound are obtained with the simple friction curve, although it has been shown that using a temperature-based friction model improves playability [
25]. The friction curve employed here for the bow is deduced from experimental measurements in the steady sliding case (e.g., at constant velocity) [
42]; it is illustrated in
Figure 4a.
2.5.3. Finger
Adding the left hand finger in the horizontal direction yields:
where
and
are defined in
Section 2.4.2, and
is a dimensionless friction coefficient.
To the authors’ knowledge, there is no experimental data allowing for the calibration of the finger (or the fingerboard) friction curve. The fingers have the joint function, along with the fingerboard, of capturing the string to reduce its speaking length, to a crude approximation. In the absence of such data, a Coulomb-like step characteristic can therefore be assumed (illustrated in
Figure 4b, where the static friction case occurs in most playing situations, but the string is capable of slipping under the finger if the left hand grip is too loose:
is a positive kinetic friction coefficient, quantifying how “sticky” the fingertip is.
is the horizontal position of the fingertip, with respect to the resting string axis. It is hypothesised that the fingertip oscillates about the top finger joint, while simultaneously damping the horizontal vibrations of the string. The temporal evolution of
can therefore be written as:
where
is a spring constant, and
is a damping coefficient. A linear damped oscillator model for the finger is chosen in the horizontal polarisation. Indeed, the choice of a more elaborate contact model such as the one used in the vertical polarisation seems unjustified; while impacts are dominant in the vertical polarisation, e.g., when hammering the string for changing notes, it is clear that collisions only have an auxiliary effect in the tangential polarisation.
Note that this version of the model, before even introducing the fingerboard, could be used to simulate the bowing of natural harmonics of the string.
2.5.4. Fingerboard
The fingerboard friction force is distributed along the whole string; if plucked particularly hard, the string’s impact on the fingerboard can tangentially translate into friction, and the string will also slide against the neck of the instrument, adding to the audible rattling effect. The string equation becomes:
where, again,
is the normal fingerboard force defined in
Section 2.4.3, and
is the friction coefficient for the fingerboard, depending on the relative velocity between the fingerboard and the string (that is, the velocity of the string itself, as the fingerboard is not moving):
Figure 5 summarises the forces at play in the horizontal polarisation.
2.6. Energy Analysis
One can derive a power balance equation for both polarisations. The transfer of this equation to discrete time provides a tool to help ensure numerical stability.
Multiplying Equation (11) by
and integrating over the length of the string, and multiplying Equations (10a) and (10b) by
and
respectively, yield the following power balance (for energy-conserving boundary conditions, such as those given in Equation (3)):
The variation of the total kinetic and potential energy
is equal to the total power
supplied to the system through external excitation (which can be negative), minus the power
withdrawn from the system through damping. The system is therefore globally energy balanced. The energy is defined as:
The power supplied through external excitation is:
The power lost through damping within the string and through collision with the neck, finger and bow is given by:
In the absence of excitation, the energy strictly decreases.
For the horizontal polarisation, multiplying Equation (22) by
and integrating over
, and multiplying Equations (18) and (21) by
and
respectively, yield the power balance:
Again, the variation of
is equal to the total power
supplied to the system in the horizontal polarisation through external excitation, minus power losses
from damping. The energy is defined as:
The power supplied or withdrawn by external excitation is:
The power lost through string damping and friction is:
Note that if , which is true for the friction characteristics of the three objects.
The total power of the full system is therefore balanced by:
A power balance of the same type as Equation (32a) is generally used as the base for another class of modelling methods, based on so-called port-Hamiltonian systems [
54]. Discretisation of such systems has recently been successfully implemented for time domain physical modelling of acoustic and electroacoustic systems [
55].
5. Discussion
This work introduces a novel two polarisation bowed string physical model, including nonlinear damped contact and friction interactions with one bow, one stopping finger, and the distributed fingerboard. An energy-balanced finite difference scheme was presented, resulting in a two-step time recursion.
The inclusion of lumped and distributed interactions with the player (through the bow and finger) and fingerboard allows for simulating full articulated gestures in a relatively instinctive and concrete way, without having to rely on somewhat abstract hypotheses — an eloquent example being the finger model, that accounts for several important phenomena that would be difficult (impossible in fact, for some) to model with a simple absorbing string termination. Here, the simple action of pushing a finger down onto the string results in damped dynamic behaviour in both polarisations, variations of the string’s speaking length, possible slipping of the string while captured, while the portion of the string between the nut and finger is still realistically oscillating, and responding to the excitation.
However, an important aspect of gestural control in bowed string playing resides in real-time adjustments of playing parameters during note production. The musician relies on immediate feedback from his instrument, adapting its playing accordingly. Our model, even with the aforementioned possible optimisations, does not run in real-time, making gesture design rather difficult. An interesting study could make use of recorded data from sensors during various gestures, feeding them as time series into the model, rather than our current breakpoint functions. This would help calibrate the model, on the string side as well as for the gestural functions [
15,
35].
The adaptation of this work to the more realistic case of multiple fingers (and, why not, multiple bows) is trivial, as well as the design of a multiple string environment. The mutual coupling of such strings is the obvious next step, moving towards the design of a full instrument, where strings communicate with a flexible body and with each other through a bridge. The simulated body will eventually take a great part in both the virtual instrument’s playability, introducing vibrations feeding back into the strings, and the realism of the synthetic sound; to address the latter, and get a glimpse at the potential of a full instrument model, we have convolved a dry output signal from this string model with the impulse response of a cello body, a principle that is still used to this day for high quality sound synthesis [
58]. The resulting sound example can be found online, amongst other relevant samples obtained from the model [
41].