Analysis and Experimental Research of a Multilayer Linear Piezoelectric Actuator
Abstract
:1. Introduction
2. Structure and Working Principle
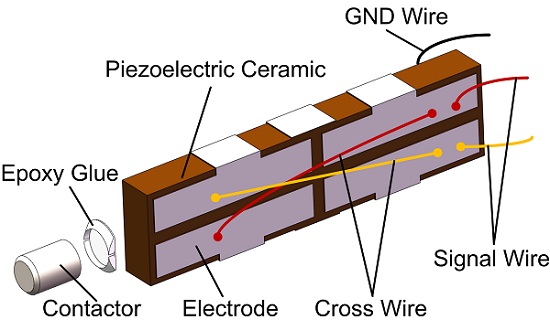
2.1. The Structure of the Piezo-Vibrator
2.2. The Working Principle of the MLPA
3. Design and Analysis
- (1)
- Elastic matrix in flexibility form SE (unit: 10−12 m2/N):
- (2)
- The matrix in d form used in ANSYS is (unit: pC/N):
- (3)
- Relative permittivity matrix (εT/ε0):
4. Results and Discussion
4.1. Harmonic Response Characteristics
4.2. Mechanical Characteristics
4.3. Temperature Characteristics
5. Conclusions
Acknowledgements
Author Contributions
Conflicts of Interest
References
- Snitka, V. Ultrasonic actuators for nanometre positioning. Ultrasonics 2000, 38, 20–25. [Google Scholar] [CrossRef]
- Bein, T.; Breitbach, E.J.; Uchino, K. A linear ultrasonic motor using the first longitudinal and the fourth bending mode. Smart Mater. Struct. 1997, 6, 619–627. [Google Scholar] [CrossRef]
- Chu, X.C.; Wang, J.W.; Yuan, S.M.; Li, L.T.; Cui, H.C. A screw-thread-type ultrasonic actuator based on a langevin piezoelectric vibrator. Rev. Sci. Instrum. 2014, 85, 065002. [Google Scholar] [CrossRef] [PubMed]
- Liu, Y.X.; Chen, W.S.; Feng, P.L.; Liu, J.K. A linear piezoelectric actuator using the first-order bending modes. Ceram. Int. 2013, 39, S681–S684. [Google Scholar] [CrossRef]
- Yuan, S.M.; Zhu, C.; Chu, X.C.; Zhao, Y.Q.; Amin, M.; Fan, Y.L. A novel linear piezoelectric actuator with two working principles of standing and traveling wave vibration mode. AIP Adv. 2015, 5, 107213. [Google Scholar] [CrossRef]
- Li, X.T.; Chen, J.G.; Chen, Z.J.; Dong, S.X. A high-temperature double-mode piezoelectric ultrasonic linear motor. Appl. Phys. Lett. 2012, 101, 072902. [Google Scholar] [CrossRef]
- Liu, Y.X.; Chen, W.S.; Xu, D.M.; Feng, P.L.; Liu, J.K. Improvement of a rectangle-shape linear piezoelectric motor with four driving feet. Ceram. Int. 2015, 41, S594–S601. [Google Scholar] [CrossRef]
- Yun, C.H.; Waston, B.; Friend, J.; Yeo, L. A piezoelectric ultrasonic linear micromotor using a slotted stator. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2010, 57, 1868–1874. [Google Scholar] [PubMed]
- Vyshnevsky, O.; Kovalev, S.; Wischnewskiy, W. A novel, single-mode piezoceramic plate actuator for ultrasonic linear motors. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2005, 52, 2047–2053. [Google Scholar] [CrossRef]
- Hemsel, T.; Wallaschek, J. Survey of the present state of the art of piezoelectric linear motors. Ultrasonics 2000, 38, 37–40. [Google Scholar] [CrossRef]
- Liu, Y.X.; Liu, J.K.; Chen, W.S.; Feng, P.L. A square-type rotary ultrasonic motor using longitudinal modes. J. Electroceram. 2014, 33, 69–74. [Google Scholar] [CrossRef]
- Chen, Z.J.; Li, X.T.; Chen, J.G.; Dong, S.X. A square-plate ultrasonic linear motor operating in two orthogonal first bending modes. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2013, 60, 115–120. [Google Scholar] [CrossRef] [PubMed]
- Shi, Y.L.; Zhao, C.S. A new standing-wave-type linear ultrasonic motor based on in-plane modes. Ultrasonics 2011, 51, 397–404. [Google Scholar] [CrossRef] [PubMed]
- Wan, Z.J.; Hu, H. Modeling and experimental analysis of the linear ultrasonic motor with in-plane bending and longitudinal mode. Ultrasonics 2014, 54, 921–928. [Google Scholar] [CrossRef] [PubMed]
- Friend, J.; Umeshima, A.; Ishii, T.; Nakamura, K.; Ueha, S. A piezoelectric linear actuator formed from a multitude of bimorphs. Sens. Actuators A 2004, 109, 242–251. [Google Scholar] [CrossRef]
- Saigoh, H.; Kawasaki, M.; Maruko, N.; Kanayama, K. Multilayer piezoelectric motor using the first longitudinal and the second bending vibrations. Jpn. J. Appl. Phys. 1995, 34, 2760–2764. [Google Scholar] [CrossRef]
- Funakubo, T.; Tsubata, T.; Taniguchi, Y.; Kumei, K.; Fujimura, T.; Abe, C. Ultrasonic linear motor using multilayer piezoelectric actuators. Jpn. J. Appl. Phys. 1995, 34, 2756–2759. [Google Scholar] [CrossRef]
- Ganor, Z.; Rafaeli, I.; Shiv, L.; Karasikov, N. Multilayer Piezoelectric Motor. U.S. Patent 7,075,211, 31 May 1999. [Google Scholar]
- Nanomotion. Available online: http://www.Nanomotion.Com/wp-content/uploads/2015/09/hr00458000–00-hr-motor-user-manual.Pdf (accessed on 3 September 2015).
- Ueha, S.; Tomikawa, Y. Ultrasonic motors: Theory and applications; Oxford University Press: London, UK, 1994. [Google Scholar]
- Guo, M.S.; Dong, S.X.; Ren, B.; Luo, H.S. A double-mode piezoelectric single-crystal ultrasonic micro-actuator. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2010, 57, 2596–2600. [Google Scholar] [PubMed]
- Chang, L. Foundations of mems; Prentice Hall: Upper Saddle River, Bergen, NJ, USA, 2011. [Google Scholar]
- Guo, M.S.; Hu, J.H.; Zhu, H.; Zhao, C.S.; Dong, S.X. Three-degree-of-freedom ultrasonic motor using a 5-mm-diameter piezoelectric ceramic tube. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2013, 60, 1446–1452. [Google Scholar]















| Zone | 1 | 2 | 3 | 4 |
|---|---|---|---|---|
| d33 (pC/N) | 2336 | 2338 | 2252 | 2236 |
| C0 (nF) | 28.5 | 28.7 | 27.9 | 28.0 |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yuan, S.; Zhao, Y.; Chu, X.; Zhu, C.; Zhong, Z. Analysis and Experimental Research of a Multilayer Linear Piezoelectric Actuator. Appl. Sci. 2016, 6, 225. https://doi.org/10.3390/app6080225
Yuan S, Zhao Y, Chu X, Zhu C, Zhong Z. Analysis and Experimental Research of a Multilayer Linear Piezoelectric Actuator. Applied Sciences. 2016; 6(8):225. https://doi.org/10.3390/app6080225
Chicago/Turabian StyleYuan, Songmei, Yanqiang Zhao, Xiangcheng Chu, Cong Zhu, and Zuojin Zhong. 2016. "Analysis and Experimental Research of a Multilayer Linear Piezoelectric Actuator" Applied Sciences 6, no. 8: 225. https://doi.org/10.3390/app6080225
APA StyleYuan, S., Zhao, Y., Chu, X., Zhu, C., & Zhong, Z. (2016). Analysis and Experimental Research of a Multilayer Linear Piezoelectric Actuator. Applied Sciences, 6(8), 225. https://doi.org/10.3390/app6080225