1. Introduction
With the current rapid economic growth, vehicle ownership is fast increasing, accompanied by more than one million traffic accidents per year worldwide. According to statistics, about 89.8% of accidents are caused by driver’s wrong decision-making [
1]. So, in order to alleviate traffic accidents, autonomous vehicles have been the world’s special attention for its non-driver’s participation. Key issues in researching autonomous vehicle include autonomous positioning, environmental awareness, driving decision-making, motion planning, and vehicle control [
2]. As an important manifestation of the intelligent level of autonomous vehicles, the driving decision-making has currently become the focus and difficulty for experts in the study of autonomous vehicle [
3]. For autonomous vehicle, it needs to rely on driving decision-making mechanism (DDM) to decide accurate driving strategy [
4]. Collecting and extracting traffic scene feature by sensors and based on the driving rules, it could not only make accurate driving decisions, but also drive safely in complex traffic environment.
In recent years, many scholars have devoted themselves to the research of DDM for autonomous vehicles. Suh et al. [
5] established vehicles’ desired steering angle model and longitudinal acceleration model based on vehicle states, and developed a control algorithm for the driving model. Wang et al. [
6] established a DDM for car following, free driving, and lane changing, with the decision tree algorithm only considering vehicles’ running states on the road. To improve the disadvantage of lacking flexibility existing in the decision tree algorithm, Zheng et al. [
7] used traditional artificial neural network to substitute the decision tree algorithm and trained an ANN (Artificial neural networks) driving decision-making model. Noh and An [
8] presented a driving decision-making framework for automated driving in highway environment, which considers the interactions between the subject and surrounding vehicles. The previous research works mainly took vehicle states as the reference indexes of DDM, and ignored the influence of road conditions on the driving decision-making.
The empirical studies show that road conditions have a great influence on driving decision-making, including weather-related and road geometry related factors [
9,
10]. For example, reducing road visibility will change the traffic flow dynamics [
11], and changing the geometric layout of the road will easily lead to changes in driving behavior [
12]. Hamdar et al. [
10] analyzed the impact of road conditions on vehicles’ longitudinal operation, and found that extreme environmental conditions could increase the extent to which a vehicle deviated from normal driving behavior. Hoogendoorn et al. [
11] conducted a series of driving simulations and found that driving in foggy weather led to the lower speed and acceleration, as well as to consider a larger distance from the lead vehicle. Broughton et al. [
13] studied the car following decision-making under three visibility conditions, and the results showed that low visibility could reduce driver’s risk identification ability. Wang et al. [
14] analyzed the impact of road curvature and slope on car following behavior. They found that when driving on road with different slopes and curvature, the car-following characteristics of vehicles varied greatly, and then established a car following model while considering curve and slope. Olofsson et al. [
15] investigated optimal maneuvers for vehicles on different road surfaces, such as asphalt, snow, and ice, and found that there were fundamental differences in the optimal maneuvers depending on tire-road characteristics. Previous studies have shown that driving in abnormal road conditions would increase the incidence of traffic accidents that are caused by incorrect driving behavior. So, road conditions, including road curvature, slope, visibility, and friction coefficient, are important parameters for DDM.
At present, most researches use neural network, decision tree model, and mathematical model to build DDM, but these methods need a large sample size or workload, and their prediction accuracy needs to be improved [
5,
6,
7,
8]. Support Vector Machine (SVM) is a widely accepted machine learning method with strong generalization ability; it can use nonlinear methods to map the variables to be classified (SVC, support vector machine classification) or regressed (SVR, support vector machine regression) into higher or more infinite dimensional feature spaces. But, in the classification problem, SVR adopts the same principle as SVC, and SVR can predict the value of infinite possible output. In addition, the tolerance margin is set up in SVR to approximate the most accurate classification results [
16]. Although SVR is more complex than SVC, it has better flexibility in solving the multi-classification problem. Therefore, in this paper, the SVR algorithm is used to predict the multi-driving decision, and the output threshold range is set for each driving decision. In the research of driving decision, SVR is mainly used to car following behaviors [
17,
18], driving risk assessment [
19], and so on. At present, most researches use SVR to solve the problems by specifying the kernel functions directly [
17,
18,
19], but sometimes it may be found that the kernel function does not match the target problem. Therefore, in order to make the objective problem automatically choose the optimal kernel function, a new kernel function is proposed to optimize the SVR model.
So, in this paper, by simultaneously referring vehicle states and road conditions, an optimized SVR model is developed to obtain the inherent complexity of driving decisions, including car following, lane changing, and free driving. Specifically, this study makes the following contributions:
- (1)
A detailed analysis of DDM for autonomous vehicles is conducted, which suggests that the control maneuvers of autonomous vehicle depend on the extracted traffic environment feature, not only including vehicle states, but also road conditions.
- (2)
A SVR model, optimized by a weighted hybrid kernel function and particle swarm optimization (PSO) algorithm, is developed to establish DDM for autonomous vehicle. In order to validate the effectiveness of the optimized SVR model, the SVR model with a single RBF kernel function and BP neural network (BPNN) model are tested to compare with it.
- (3)
By comparing the reasoning results of DDM with different reference index combinations, and by the sensitivity analysis, the effect of road conditions on driving decisions is quantitatively evaluated.
2. The Driving Decision-Making Process of Autonomous Vehicle
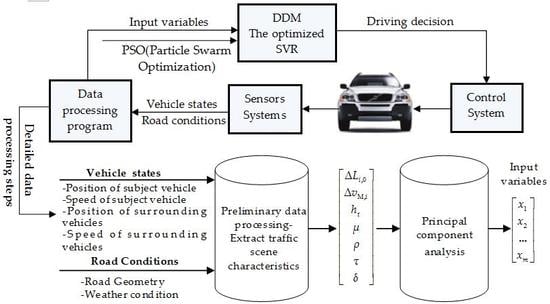
As shown in
Figure 1, with the sensor equipment, the autonomous vehicle can sense and collect traffic information, including vehicle states and road conditions in real time, to input them into the designed data processing program for some data processing to obtain the input variables of DDM.
According to these input variables, the DDM searches the relevant information and matches the accurate driving decision with the learning experiences, and then transmits the decision order to the control system. These learning experiences refer to the driving decision-making rules in DDM that are obtained by learning a lot of real driving experience. Then, the control system will control the actuators (include the steering system, pedals, and automatic gearshift) to carry on with the corresponding operation.
In the whole process of information collection, transmission, and execution, the DDM plays a key role, which is the central system to control the autonomous vehicle. The types of driving decision DDM outputs include free driving, car following, and lane changing. Its input variables are obtained through the preliminary data processing for extracting traffic scenario characteristics as reference indexes and the further data fusion. The method of data fusion adopted in this paper is Principal Component Analysis (PCA). The whole detailed data processing steps in the data processing program are described in
Figure 2.
The schematic diagram of vehicle states on a road is shown in
Figure 3. All of the above obtained reference indexes in
Figure 2 are described as follows:
/(m): The gap difference between and safe distance , and refers to the distance between the subject vehicle M and vehicle , ;
/(m/s): The relative speed between vehicle M and vehicle ;
/(s): The time headway of current lane;
: Road adhesion coefficient, dimensionless;
/(m−1): Road curvature;
: Road slope, percentage; and,
/(m): Road visibility.
2.1. Support Vector Machine Regression Model
SVR model is a kind of machine learning method based on statistical learning theory, which can improve the generalization ability of learning machine by seeking the minimum structural risk [
16,
20]. So, SVR model has been widely applied and developed in the fields of pattern recognition, regression analysis, and sequence prediction [
18,
21].
Let
be a set of
training samples, each of samples
is the input variable, which is obtained from traffic environment features.
is the output driving decision corresponding to
. These training samples are fitted by
, and all of the fitted results must be satisfied with error accuracy
, i.e.,:
According to the minimization criteria of structural risk,
should make
minimum. When considering the exiting fitted errors, the relaxation factors are introduced as
,
. The best regression result can be derived from the minimum extreme value of the following function:
where
is the penalty factor value,
.
Then, adopt the dual principle, and set the Lagrange multiplier
,
to establish the Lagrange equation. Through drafting the parameters
,
,
,
and making the drafted formulas equal to 0, the regression coefficient
and constant term
can be obtained:
After that, the results are substituted into the function
to get the regression function:
Finally, the original samples are mapped into a high-dimensional feature space with a kernel function
, and calculate the parameters with the same method, as above. The obtained non-linear regression function is:
The common kernels are showed as following:
Polynomial kernel function:
Radial basis function:
Sigmoid kernel function:
Where the dot denotes the inner-product operation in Euclidean space,
is the degree of polynomial kernel,
is the constant term determining the width of RBF kernel [
18]. With different kernels, it can be structured by different regression surfaces, then different training results may be gotten on driving decision-making. So, it is important to select the proper kernel function and kernel parameters in the SVR model.
2.2. The Optimized Support Vector Machine Regression Model
2.2.1. The Selection of Kernel Function
In the research field of SVR model, the selection of kernel function type is the most popular research problem. The kernel function adopted by most of SVR research is the RBF kernel function. But, for different specific problems, the selected kernel function can reflect some of the characteristics of the problem itself [
22]. The kernel function specified by researchers based on experience may not be the best choice for specific problems. So, this requires some ways to choose the optimal kernel function for them. In this paper, in order to avoid complexity and one-sidedness of the selection, and to give full play to the benefits that are brought by various kernel functions for the DDM, a weighted hybrid kernel function is proposed:
where
,
,
, respectively, refer to the weight factor and exponential factor corresponding to each kernel function. Then, combine the exponential factor
,
with
and
respectively, we can simplify this formula:
The weighting factor needs to be satisfied:
When , it represents that the corresponding kernel function does not play a role in DDM. When , and , then the expression of the formula is similar with the primitive type of Polynomial Kernel.
2.2.2. Parameter Optimization
Particle swarm optimization (PSO) algorithm is a new evolutionary and iterative optimization algorithm developed in recent years. PSO algorithm is also started from the random solution and the quality of its solution is evaluated by the fitness. It finds the global optimum following the optimal particles in the solution space [
23]. PSO algorithm has a fast convergence rate, and can avoid falling into the local optimum [
24,
25]. So, in this paper, we adopt PSO algorithm to optimize the undetermined parameters of the SVR model and the weighted hybrid kernel function.
In the PSO algorithm, particles dynamically adjust their positions in the
-dimensional space through their individual and peer flight experience. In
-dimensional space, the number of particles is
, and the position of particle
can be represented as
, and its flying speed is
. The best position visited by the particle
so far can be noted as the particle best, i.e.,
, and the best position found by all the particles so far can be noted as the global best, i.e.,
. At every moment
, the particle will adjust its speed and position by:
where
,
,
is the limited maximum flying speed, and
is the uniform random number on the interval
, it can increase the searching randomness of particles based on the
Pbest and the
Gbest.
Then, the PSO-SVR parameter optimization architecture is established in
Figure 4. We set the updated step factor as
and the positive acceleration coefficients of particle as
. The limited maximum flying speed
is set to 100, and the number of particles
is 50. The number of undetermined parameters is 9, including
,
in selecting kernel function type, parameters of each single kernel function
,
,
,
,
,
, and SVR penalty factor
, it is represented as the dimension of the particle space. The parameter of kernel function
and penalty factor
are limited in the value range (−10, 10).
The optimization steps are given as follows:
- Step 1
randomly initialize the positions and speeds of all particles;
- Step 2
the fitness value of each particle is calculated according to the fitness function of driving decision problem;
- Step 3
respectively compare the fitness value of each particle with their own and . If the fitness value is larger than , then update with the fitness value. If the fitness value is larger than , then update with the fitness value;
- Step 4
for each update, reset the SVR penalty factor to create a larger research space for particles, avoid falling into the local area of current optimal value;
- Step 5
update the position and speed of each particle according to Formulas (8) and (9); and,
- Step 6
when the number of iterations reaches the maximum set, stop it and output the optimal parameters. Otherwise, return to Step 2.
In this paper, set the training accuracy as the fitness function in the optimized process. In order to evaluate the predicting effect of model for each driving decision, the average absolute error
and relative mean square error
are selected as the comprehensive evaluation indexes. The former can reflect the degree of deviation between reasoning and measured values, and the latter is the changing embodiment of the error values, which reflects the output stability of SVR model.
3. Experimental Set-Up
A driving experiment needs to be set up to collect relevant data for training the optimized SVR model. Driving simulation is an alternative on-road experiment when the driver desires to use more controllable traffic scenarios to manipulate under certain experimental conditions. By adjusting the light, brightness, motion, audio, etc. in the simulator, it can represent a real traffic scene and an actual vehicle for the driver, which is used to study driving behaviors safely. From the output data, we can obtain the trajectory data of the subject and surrounding vehicles, which are useful to analyze driving decisions.
3.1. Driving Simulator
Driving simulation experiment is performed using the UC-win/Road 12.0 driving simulator platform (12.0 version, Fulamba Software Technology Co., Ltd., Shanghai, China, 2016) at the intelligent transportation experimental center of Transportation College in Shandong University of Science and Technology, which is shown in
Figure 5. The hardware is made up of three networked computers and some interfaces, such as the steering system, pedals and the automatic gearshift. The traffic environment is projected onto a large visual screen (Fulamba Software Technology Co., Ltd., Shanghai, China) (this big screen is made up of 3 sub-screens), which can provide a 135° field of view. The resolution of visual scene is 1920 × 1080, the refresh rate of the scene is 20–60 Hz depending on the complexity traffic environment. The simulator can record the position coordinates, speed, acceleration of the subject vehicle, and the surrounding vehicle in real time.
3.2. Participants
A total of 31 drivers with different driving experiences are recruited for experiment, including 19 male and 12 female drivers. Before performing driving simulation experiments, a survey for all of the participants is conducted, which is mainly focused on personal driving habits, driving experience, car accident history, physical and psychological status, etc. The average age of the participants is 25.7 years old (std is 3.91 years), ranging from 23 to 37 years. All of the participants have a qualified driver’s license, and more than five years of driving experience (std is 4.33 years). None of participant has any visual and psychological problems. Among 31 participants, three participants (two males, one female) had car crashes in the past five years. The participants are trained to be familiar with the driving simulated operation and to complete the driving simulation on all the traffic environments as required.
3.3. Driving Scenario Setting
A two-way with four-lane urban road section is established for this experiment, as shown in
Figure 5. Setting different parameters for vehicles, roads, and traffic, we can establish different traffic simulated scenarios. Set all the vehicles running on these scenarios as standard cars, and the traffic density range to 4–32 veh/km (note: 4–16 veh/km is the low density range, 16–28 veh/km is the middle density range, and 28–32 veh/km is the high density range). The traffic flow is running randomly at each density range with a desired speed of 40–50 km/h. The reference values of the road parameters are shown in
Table 1, and the initial set of road parameters are standard values, i.e., (
μ,
ρ,
τ,
δ) = (0.75, 0, 0, 1000). The data acquisition frequency is 10 Hz.
3.4. Data Acquisition and Preprocessing
3.4.1. Data Acquisition
The collected data include driving trajectory data of the subject and its surrounding vehicles, their speeds and road environment parameters. According to the following method, the useful driving trajectory data of each driving decision are extracted and classified into the driving decision data set:
- (1)
Lane changing: The driving trajectory data of 10 s before implementing lane changing are recorded in lane changing data set.
- (2)
Car following: The driving trajectory data within the 50 m gaps between the subject and its leading vehicle are recorded in car following data set.
- (3)
Free driving: The driving trajectory data beyond 50 m gaps between the subject and its leading vehicle, and the driving trajectory data output when the subject vehicle with the desired speed are recorded in free driving data set.
After data classification and statistics, a total of 3211 groups of free driving data, 5312 groups of car following data, and 1009 groups of lane changing data are obtained. Each group of driving decision data includes one group of the driving trajectory data, together with their corresponding speeds and the road environment parameters.
3.4.2. Preliminary Data Process
In the preliminary data process, the data contained in all driving decision data sets are calculated to obtain the driving decision samples. From the driving trajectory data, we can obtain , , , and the driving decision (free driving, car following or lane changing), from the speed information, we can obtain , , and , from the road environment parameters, we can obtain the values of μ, ρ, τ, δ. One sample includes one reference index vector and its corresponding driving decision.
3.4.3. The Output and Input Variables of the Optimized SVR Model
(1) The output variables
In this paper, the output variable of the optimized SVR model is a driving decision, may be free driving, car following, or lane changing. We assign the represented values and the output threshold ranges to all of the driving decisions, as seen in
Table 2. For example, if an output value of DDM falls within the threshold range (−1.5, 0.5), it represents that the driving decision is free driving.
(2) The input variables
Solving practical problems often need to collect a lot of indexes to reflect more information about the research object. If the correlation between these indexes is high, then the information reflected from them will have a certain overlap, which will increase the complexity of processing information. To solve this problem, Principal Component Analysis (PCA) is proposed to analyze data indexes and obtain the needed input variables [
26].
PCA is a statistical analysis method. It can transform multiple correlated indexes into a few of uncorrelated indexes. The comprehensive indexes, called the principal components, will keep the original indexes information as much as possible. If there is a
-dimensional random vector
, using PCA, the
reference indexes can be transformed into a set of uncorrelated principal indexes
as their principal components, as seen in (14).
Then,
principal components need to be selected from above
principal components to adequately reflect the information represented by
. The number of principal components
depends on the cumulative contribution rate of the variance
.
where
is the eigenvalue of
.
Usually, when , these principal components can adequately reflect the information of the original reference indexes.
Then, we use PCA to make the correlation analysis of 11 reference indexes through 200 sets of samples. The analysis process of PCA is shown in
Figure 6. The calculated results of PCA for each principal component are shown in
Figure 7. According to the cumulative contribution rate of the variance of each principal component, the first five principal components
are selected as the input variables of the optimized SVR model.
5. Conclusions
In this paper, a SVR model was developed to make accurate driving decisions for autonomous vehicle. Our model was optimized by a weighted hybrid kernel function and a PSO algorithm. Road conditions and vehicle states were simultaneously as the reference indexes of DDM. The driving decisions that were made by DDM included free driving, car following, and lane changing. Then, driving simulated experiments with different traffic environments were executed to extract the driving decision samples. The optimized SVR model was trained and validated with the training and testing samples to establish DDM. Our model was compared with: (1) a SVR model with RBF kernel function, and (2) BPNN model. The comparison results showed that the accuracy of our optimized SVR model was the best, with more than 92% accuracy. Besides, the results also showed that our optimized SVR model had a better performance in free driving and car following with 93.1% and 94.7% of accuracy, respectively, than lane changing decision with 89.1% of accuracy.
Finally, we investigated the effect of road conditions on the accuracy of DDM and quantified their effects on each driving decision through the sensitive analysis. The results showed that road conditions almost had almost no influence on driving decisions with high traffic density range, and had the greatest influence with low traffic density range. In the low and middle traffic density, road visibility has the greatest effect on the driving decisions, then followed by , , and . To some extent, the verified results were consistent with the actual driving experience, which indicated the reasonability of the obtained DDM with added road conditions.
Even though the DDM based on the optimized SVR model is able to reason driving decisions, and outperforms other models that are proposed in this paper, there are still some weak points and limits, such as the sample size of lane changing decision is smaller than that of car following and free driving, and that the DDM has not yet been implemented in real road environment, we will improve them in the future. In addition, future research will focus on establishing a DDM used in dangerous driving environments, for example, if a pedestrian or vehicle suddenly present in front of the subject vehicle, then the subject vehicle should make proper driving decision, like steering, braking, or steering and braking.