A Bio-Inspired Control Strategy for Locomotion of a Quadruped Robot
Abstract
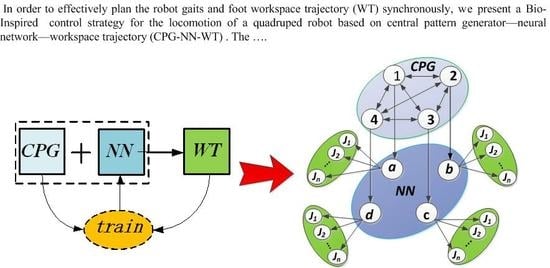
:1. Introduction
2. The Foot WT Planning
2.1. Modeling and Kinematics Analysis of a Quadruped Robot
2.2. Foot WT Planning
3. Improved CPG
3.1. Modified CPG Oscillator Unit Model
3.2. Improved CPG Control Model
- (1)
- In order to adjust the gait period and duty factor directly and independently, the frequency of the Hopf oscillator is modified as Equation (8).
- (2)
- Parameter is introduced as coupling intensity coefficient among the CPG oscillator units to control the gait transition speed and waveform.
- (3)
- Multiple feedbacks with their corresponding reflex coefficients are simultaneously introduced into the two states (x and y) of the CPG oscillator unit. With the reflex information matrix and reflex coefficient vector, a clear way of expression and implementation is provided to realize the biological reflex modeling.
4. CPG-NN-WT-Based Control Strategy
4.1. CPG-NN-WT Control Model
4.2. Realization of CPG-NN-WT Control Model
5. Results and Discussion
5.1. Virtual Prototype Simulation
5.2. Experiment with a Real Quadruped Robot
6. Conclusions
- (1)
- An improved foot WT based on the compound cycloid is planned with advantages of low mechanical impact, smooth movement and sleek trajectory.
- (2)
- An improved CPG based on Hopf oscillators put forward in this paper can effectively realize the smooth gait planning by adjusting its internal parameters.
- (3)
- A biologically inspired control strategy based on CPG-NN-WT is presented for locomotion control of a quadruped robot, which can effectively integrate the advantages of CPG-based method with WT-based method. Besides, the presented control strategy provides an effective way to realize the multi-joint coordination control within a leg, since the NN has the capability of multi-input and multi-output. Furthermore, theoretically, the CPG-NN-WT control model can output any desired periodic WT, which depends only on the complexity of the NN.
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Ijspeert, A.J. Central pattern generators for locomotion control in animals and robots: A review. Neural Netw. 2008, 21, 642–653. [Google Scholar] [CrossRef] [PubMed]
- Kalakrishnan, M.; Buchli, J.; Pastor, P.; Mistry, M.; Schaal, S. Learning, planning, and control for quadruped locomotion over challenging terrain. Int. J. Robot. Res. 2011, 30, 236–258. [Google Scholar] [CrossRef]
- Kalakrishnan, M.; Buchli, J.; Pastor, P.; Mistry, M.; Schaal, S. Fast, robust quadruped locomotion over challenging terrain. In Proceedings of the 2010 IEEE International Conference on Robotics and Automation, Anchorage, AK, USA, 3–7 May 2010. [Google Scholar]
- Lei, J.; Wang, F.; Yu, H.; Wang, T.; Yuan, P. Energy efficiency analysis of quadruped robot with trot gait and combined cycloid foot trajectory. Chin. J. Mech. Eng. 2014, 27, 138–145. [Google Scholar] [CrossRef]
- Xie, H.; Shang, J.; Ahmadi, M. Adaptive control strategies for quadruped robot on unperceived slopedterrain. Int. J. Robot. Autom. 2015, 30, 90–111. [Google Scholar]
- Li, J.; Wang, J.; Yang, S.X.; Zhou, K.; Tang, H. Gait Planning and Stability Control of a Quadruped Robot. Comput. Intell. Neurosci. 2016, 2016, 9853070. [Google Scholar] [CrossRef] [PubMed]
- Qian, X.; Huang, H.; Chen, X.; Huang, T. Generalized Hybrid Constructive Learning Algorithm for Multioutput RBF Networks. IEEE Trans. Cybern. 2017, 47, 3634–3648. [Google Scholar] [CrossRef] [PubMed]
- Matos, V.; Santos, C.P. Omnidirectional locomotion in a quadruped robot: A CPG-based approach. In Proceedings of the 2010 IEEE/RSJ International Conference on Intelligent Robots and Systems, Taipei, Taiwan, 18–22 October 2010; Volume 6219, pp. 3392–3397. [Google Scholar]
- Koco, E.; Mutka, A.; Kovacic, Z. New parameterized foot trajectory shape for multi-gait quadruped locomotion with state machine-based approach for executing gait transitions. In Proceedings of the 2014 22nd Mediterranean Conference on Control and Automation, Palermo, Italy, 16–19 June 2014; pp. 1533–1539. [Google Scholar]
- Wu, Q.; Liu, C.; Zhang, J.; Chen, Q. Survey of locomotion control of legged robots inspired by biological concept. Sci. China Ser. F Inf. Sci. 2009, 52, 1715–1729. [Google Scholar] [CrossRef]
- Tran, D.T.; Koo, I.M.; Lee, Y.H.; Moon, H.; Park, S.; Koo, J.C.; Choi, H.R. Central pattern generator based reflexive control of quadruped walking robots using a recurrent neural network. Robot. Auton. Syst. 2014, 62, 1497–1516. [Google Scholar] [CrossRef]
- Matsuoka, K. Mechanisms of frequency and pattern control in the neural rhythm generators. Biol. Cybern. 1987, 56, 345–353. [Google Scholar] [CrossRef] [PubMed]
- Kimura, H.; Fukuoka, Y.; Hada, Y.; Takase, K. Adaptive Dynamic Walking of a Quadruped Robot on Irregular Terrain Using a Neural System Model; Springer: Berlin/Heidelberg, Germany, 2003. [Google Scholar]
- Tsujita, K.; Toui, H.; Tsuchiya, K. Dynamic turning control of a quadruped locomotion robot using oscillators. Adv. Robot. 2005, 19, 1115–1133. [Google Scholar] [CrossRef]
- Sun, X. Kuramoto Model; Springer: New York, NY, USA, 2013. [Google Scholar]
- Acebron, J.A.; Bonilla, L.L.; Vicente, C.J.P.; Ritort, F.; Spigler, R. The Kuramoto model: A simple paradigm for synchronization phenomena. Rev. Mod. Phys. 2005, 77, 137–185. [Google Scholar] [CrossRef] [Green Version]
- Zhang, J.; Masayoshi, T.; Chen, Q.; Liu, C. Dynamic Walking of AIBO with Hopf Oscillators. Chin. J. Mech. Eng. 2011, 24, 612–617. [Google Scholar] [CrossRef]
- Hu, Y.; Liang, J.; Wang, T. Parameter Synthesis of Coupled Nonlinear Oscillators for CPG-Based Robotic Locomotion. IEEE Trans. Ind. Electron. 2014, 61, 6183–6191. [Google Scholar] [CrossRef]
- Yu, H.; Gao, H.; Ding, L.; Li, M.; Deng, Z.; Liu, G. Gait Generation With Smooth Transition Using CPG-Based Locomotion Control for Hexapod Walking Robot. IEEE Trans. Ind. Electron. 2016, 63, 5488–5500. [Google Scholar] [CrossRef]
- Kwon, O.; Jeon, K.S.; Park, J.H. Optimal trajectory generation for biped robots walking up-and-down stairs. J. Mech. Sci. Technol. 2006, 20, 612–620. [Google Scholar] [CrossRef]
- Ma, S.; Tomiyama, T.; Wada, H. Omnidirectional static walking of a quadruped robot. IEEE Trans. Robot. 2005, 21, 152–161. [Google Scholar] [CrossRef]
- Liu, C.J.; Wang, D.W.; Chen, Q.J. Locomotion Control Of Quadruped Robots Based on Workspace Trajectory Modulations. Int. J. Robot. Autom. 2012, 27, 345–354. [Google Scholar] [CrossRef]
- Sakakibara, Y.; Kan, K.; Hosoda, Y.; Hattori, M. Foot trajectory for a quadruped walking machine. In Proceedings of the IROS ‘90 IEEE International Workshop on Intelligent Robots and Systems ‘90 ‘towards A New Frontier of Applications’, Ibaraki, Japan, 3–6 July 1990; Volume 1, pp. 315–322. [Google Scholar]
- Wang, L.; Wang, Z.; Wang, S.; He, Y. Strategy of Foot Trajectory Generation for Hydraulic Quadruped Robots Gait Planning. J. Mech. Eng. 2013, 49, 39–44. [Google Scholar] [CrossRef]
- Righetti, L.; Ijspeert, A.J. Design Methodologies for Central Pattern Generators: An Application to Crawling Humanoids. Robotics: Science and Systems II; University of Pennsylvania: Philadelphia, PA, USA, 2006. [Google Scholar]
- Righetti, L.; Ijspeert, A.J. Pattern generators with sensory feedback for the control of quadruped locomotion. In Proceedings of the IEEE International Conference on Robotics and Automation, Pasadena, CA, USA, 19–23 May 2008; pp. 819–824. [Google Scholar]
- Smith, J.A. Galloping in an Underactuated Quadrupedal Robot. Int. J. Robot. Autom. 2015, 30. [Google Scholar] [CrossRef]
- Ren, J.; Xu, H.; Gan, S.; Wang, B. CPG modele design based on hopf oscillator for hexapod robots gait. CAAI Trans. Intell. Syst. 2016, 11, 627–634. [Google Scholar]
- Li, H.; Han, B.; Luo, Q. Inter-limb and intra-limb coordination control of quadruped robots. J. Beijing Inst. Technol. 2015, 4, 478–486. [Google Scholar]
- Lee, N.K.; Wang, D. Realization of Generalized RBF Network. Appl. Spectrosc. 2003, 62, 341–344. [Google Scholar]
- Nabney, I.T. Efficient training of RBF networks for classification. Int. J. Neural Syst. 2004, 14, 201–208. [Google Scholar] [CrossRef] [PubMed]
- He, W.; Chen, Y.; Yin, Z. Adaptive Neural Network Control of an Uncertain Robot With Full-State Constraints. IEEE Trans. Cybern. 2015, 46, 620–629. [Google Scholar] [CrossRef] [PubMed]
- Chen, H.; Yu, G.; Xia, H. Online Modeling With Tunable RBF Network. IEEE Trans. Cybern. 2013, 43, 935–947. [Google Scholar] [CrossRef] [PubMed]
- Fortuna, L.; Arena, P.; Balya, D.; Zarandy, A. Cellular neural networks: A paradigm for nonlinear spatio-temporal processing. IEEE Circuits Syst. Mag. 2001, 1, 6–21. [Google Scholar] [CrossRef]





















| Link No. i | Joint Variable θi (Rad) | Offset di (mm) | Link Length ai−1 (mm) | Link Angle ai−1 (Rad) |
|---|---|---|---|---|
| 1 | θ1 + θh | 0 | l1 | 0 |
| 2 | θ1 + θk | 0 | l2 | 0 |
| Gait | Gait Matrix (Phase Relationships) |
|---|---|
| walk | (0, π, π/2, 3π/2) |
| trot | (0, π, 0, π) |
| pace | (0, π, π, 0) |
| gallop | (0, 0, π, π) |
| Parameters | Value |
|---|---|
| size: L × W × H (mm) | 500 × 200 × 405 |
| mass (kg) | 4 |
| l1 (mm) | 150 |
| l2 (mm) | 150 |
| hip joint range | (−π, π) |
| knee joint range | (−π, π) |
| Parameters | Value |
|---|---|
| size: L × W × H (mm) | 400 × 220 × 420 |
| mass (kg) | 3.6 |
| l1 (mm) | 150 |
| l2 (mm) | 150 |
| hip joint range | (−π, π) |
| knee joint range | (−π, π) |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zeng, Y.; Li, J.; Yang, S.X.; Ren, E. A Bio-Inspired Control Strategy for Locomotion of a Quadruped Robot. Appl. Sci. 2018, 8, 56. https://doi.org/10.3390/app8010056
Zeng Y, Li J, Yang SX, Ren E. A Bio-Inspired Control Strategy for Locomotion of a Quadruped Robot. Applied Sciences. 2018; 8(1):56. https://doi.org/10.3390/app8010056
Chicago/Turabian StyleZeng, Yinquan, Junmin Li, Simon X. Yang, and Erwei Ren. 2018. "A Bio-Inspired Control Strategy for Locomotion of a Quadruped Robot" Applied Sciences 8, no. 1: 56. https://doi.org/10.3390/app8010056
APA StyleZeng, Y., Li, J., Yang, S. X., & Ren, E. (2018). A Bio-Inspired Control Strategy for Locomotion of a Quadruped Robot. Applied Sciences, 8(1), 56. https://doi.org/10.3390/app8010056