Boosting Second Harmonic Radiation from AlGaAs Nanoantennas with Epsilon-Near-Zero Materials
Abstract
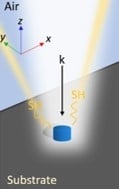
:1. Introduction
2. Results and Discussion
3. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Kuznetsov, A.I.; Miroshnichenko, A.E.; Brongersma, M.L.; Kivshar, Y.S.; Lukyanchuk, B. Optically resonant dielectric nanostructures. Science 2016, 354, 6314. [Google Scholar] [CrossRef] [PubMed]
- Smirnova, D.; Kivshar, Y.S. Multipolar nonlinear nanophotonics. Optica 2016, 3, 1241–1255. [Google Scholar] [CrossRef]
- Decker, M.; Staude, I. Resonant dielectric nanostructures: A low-loss platform for functional nanophotonics. J. Opt. 2016, 18, 103001. [Google Scholar] [CrossRef]
- Rocco, D.; Carletti, L.; Locatelli, A.; De Angelis, C. Controlling the directivity of all-dielectric nanoantennas excited by integrated quantum emitters. J. Opt. Soc. Am. B 2017, 34, 1918–1922. [Google Scholar] [CrossRef]
- Carletti, L.; Locatelli, A.; Stepanenko, O.; Leo, G.; De Angelis, C. Enhanced second-harmonic generation from magnetic resonance in AlGaAs nanoantennas. Opt. Express 2015, 23, 26544–26550. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Gili, V.F.; Carletti, L.; Locatelli, A.; Rocco, D.; Finazzi, M.; Ghirardini, L.; Favero, I.; Gomez, C.; Lemaître, A.; Celebrano, M.; De Angelis, C.; et al. Monolithic AlGaAs second-harmonic nanoantennas. Opt. Express 2016, 24, 15965–15971. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Camacho-Morales, R.; Rahmani, M.; Kruk, S.; Wang, L.; Xu, L.; Smirnova, D.A.; Solntsev, A.S.; Miroshnichenko, A.; Tan, H.H.; Karouta, F.; et al. Nonlinear Generation of Vector Beams From AlGaAs Nanoantennas. Nano Lett. 2016, 16, 7191–7197. [Google Scholar] [CrossRef] [PubMed]
- Liu, S.; Sinclair, M.B.; Saravi, S.; Keeler, G.A.; Yang, Y.; Reno, J.; Peake, G.M.; Setzpfandt, F.; Staude, I.; Pertsch, T.; et al. Resonantly Enhanced Second-Harmonic Generation Using III–V Semiconductor All-Dielectric Metasurfaces. Nano Lett. 2016, 16, 5426–5432. [Google Scholar] [CrossRef] [PubMed]
- Rocco, D.; Gili, V.F.; Ghirardini, L.; Carletti, L.; Favero, I.; Locatelli, A.; Marino, G.; Neshev, D.N.; Celebrano, M.; Finazzi, M.; et al. Tuning the second-harmonic generation in AlGaAs nanodimers via non-radiative state optimization. Photonics Res. 2018, 6, B6–B12. [Google Scholar] [CrossRef]
- Grinbalt, G.; Li, Y.; Nielsen, M.P.; Oulton, R.F.; Maier, S.A. Enhanced third harmonic generation in single germanium nanodisks excited at the anapole mode. Nano Lett. 2016, 16, 4635–4640. [Google Scholar] [CrossRef] [PubMed]
- Gili, V.F.; Ghirardini, L.; Rocco, D.; Marino, G.; Favero, I.; Roland, I.; Pellegrini, G.; Duò, L.; Finazzi, M.; Carletti, L.; et al. Metal-dielectric hybrid nanoantennas for efficient frequency conversion at the anapole mode. Beilstein J. Nanotechnol. 2018, 9, 2306–2314. [Google Scholar] [CrossRef] [PubMed]
- Timpu, F.; Sergeyev, A.; Hendricks, N.R.; Grange, R. Second-harmonic enhancement with Mie resonances in perovskite nanoparticles. ACS Photonics 2016, 4, 76–84. [Google Scholar] [CrossRef]
- Carletti, L.; Rocco, D.; Locatelli, A.; De Angelis, C.; Gili, V.F.; Ravaro, M.; Favero, I.; Leo, G.; Finazzi, M.; Ghirardini, L.; et al. Controlling second-harmonic generation at the nanoscale with monolithic AlGaAs-on-AlOx antennas. Nanotechnology 2017, 28, 114005. [Google Scholar] [CrossRef] [PubMed]
- Kruk, S.S.; Camacho-Morales, R.; Xu, L.; Rahmani, M.; Smirnova, D.A.; Wang, L.; Tan, H.H.; Jagadish, C.; Neshev, D.N.; Kivshar, Y.S. Nonlinear Optical Magnetism Revealed by Second-Harmonic Generation in Nanoantennas. Nano Lett. 2017, 6, 3914–3918. [Google Scholar] [CrossRef] [PubMed]
- Guasoni, M.; Carletti, L.; Neshev, D.; De Angelis, C. Theoretical Model for Pattern Engineering of Harmonic Generation in All-Dielectric Nanoantennas. IEEE J. Quantum Electron. 2017, 53, 1–5. [Google Scholar] [CrossRef]
- Alù, A.; Silveirinha, M.G.; Salandrino, A.; Engheta, N. Epsilon-near-zero metamaterials and electromagnetic sources: Tailoring the radiation phase pattern. Phys. Rev. B 2007, 75, 155410. [Google Scholar] [CrossRef]
- Silveirinha, M.; Engheta, N. Tunneling of Electromagnetic Energy through Subwavelength Channels and Bends using ε-Near-Zero Materials. Phys. Rev. Lett. 2006, 97, 157403. [Google Scholar] [CrossRef] [PubMed]
- Enoch, S.; Tayeb, G.; Sabouroux, P.; Guérin, N.; Vincent, P. A Metamaterial for Directive Emission. Phys. Rev. Lett. 2002, 89, 213902. [Google Scholar] [CrossRef] [PubMed]
- Lovat, G.; Burghignoli, P.; Capolino, F.; Jackson, D.R.; Wilton, D.R. Analysis of directive radiation from a line source in a metamaterial slab with low permittivity. IEE Trans. Antennas Propag. 2006, 54, 1017–1030. [Google Scholar] [CrossRef] [Green Version]
- Memarian, M.; Eleftheriades, G.V. Dipole radiation near anisotropic low-permittivity media. Prog. Electromagn. Res. 2013, 142, 437–462. [Google Scholar] [CrossRef]
- Guclu, C.; Campione, S.; Capolino, F. Array of dipoles near a hyperbolic metamaterial: Evanescent-to-propagating Floquet wave transformation. Phys. Rev. B 2014, 89, 155128. [Google Scholar] [CrossRef]
- Labelle, A.J.; Bonifazi, M.; Tian, Y.; Wong, C.; Hoogland, S.; Favraud, G.; Walters, G.; Sutherland, B.; Liu, M.; Li, J.; et al. Broadband Epsilon-near-Zero Reflectors Enhance the Quantum Efficiency of Thin Solar Cells at Visible and Infrared Wavelengths. ACS Appl. Mater. Interfaces 2017, 9, 5556–5565. [Google Scholar] [CrossRef] [PubMed]
- Tian, Y.; García de Arquer, F.P.; Dinh, C.-T.; Favraud, G.; Bonifazi, M.; Li, J.; Liu, M.; Zhang, X.; Zheng, X.; Kibria, M.G.; et al. Enhanced Solar-to-Hydrogen Generation with Broadband Epsilon-Near-Zero Nanostructured Photocatalysts. Adv. Mater. 2017, 29, 1701165. [Google Scholar] [CrossRef] [PubMed]
- Campione, S.; Albani, M.; Capolino, F. Complex modes and near-zero permittivity in 3D arrays of plasmonic nanoshells: Loss compensation using gain. Opt. Mater. Express 2011, 1, 1077–1089. [Google Scholar] [CrossRef]
- Campione, S.; Capolino, F. Composite material made of plasmonic nanoshells with quantum dot cores: Loss-compensation and epsilon-near-zero physical properties. Nanotechology 2012, 23, 235703. [Google Scholar] [CrossRef] [PubMed]
- Ciattoni, A.; Marinelli, R.; Rizza, C.; Palange, E. Epsilon-Near-zero materials in the near-infrared. Appl. Phys. B 2013, 110, 23–26. [Google Scholar] [CrossRef]
- Xiao, S.; Drachev, V.P.; Kildishev, A.V.; Ni, X.; Chettiar, U.K.; Yuan, H.-K.; Shalaev, V.M. Loss-free and active optical negative-index metamaterials. Nature 2010, 466, 735–738. [Google Scholar] [CrossRef] [PubMed]
- Naik, G.V.; Kim, J.; Boltasseva, A. Oxides and nitrides as alternative plasmonic materials in the optical range. Opt. Mater. Express 2011, 1, 1090–1099. [Google Scholar] [CrossRef]
- Naik, G.V.; Liu, J.; Kildishev, A.V.; Shalaev, V.M.; Boltasseva, A. Demonstration of Al:ZnO as a plasmonic component for near-infrared metamaterials. Proc. Natl. Acad. Sci. USA 2012, 109, 8834–8838. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Sachet, E.; Shelton, C.T.; Harris, J.S.; Gaddy, B.E.; Irving, D.L.; Curtarolo, S.; Donovan, B.F.; Hopkins, P.E.; Sharma, P.A.; Sharma, A.L.; et al. Dysprosium-doped cadmium oxide as a gateway material for mid-infrared plasmonics. Nat. Mater. 2015, 14, 414–420. [Google Scholar] [CrossRef] [PubMed]
- Vincenti, M.A.; de Ceglia, D.; Ciattoni, A.; Scalora, M. Singularity-driven second- and third-harmonic generation at ε-near-zero crossing points. Phys. Rev. A 2011, 84, 063826. [Google Scholar] [CrossRef]
- Ciattoni, A.; Spinozzi, E. Efficient second-harmonic generation in micrometer-thick slabs with indefinite permittivity. Phys. Rev. A 2012, 85, 043806. [Google Scholar] [CrossRef]
- Vincenti, M.A.; Campione, S.; de Ceglia, D.; Capolino, F.; Scalora, M. Gain-assisted harmonic generation in near-zero permittivity metamaterials made of plasmonic nanoshells. New J. Phys. 2012, 14, 103016. [Google Scholar] [CrossRef] [Green Version]
- Ciattoni, A.; Rizza, C.; Palange, E. Extreme nonlinear electrodynamics in metamaterials with very small linear dielectric permittivity. Phys. Rev. A 2010, 81, 043839. [Google Scholar] [CrossRef]
- De Ceglia, D.; Campione, S.; Vincenti, M.A.; Capolino, F.; Scalora, M. Low-damping epsilon-near-zero slabs: Nonlinear and nonlocal optical properties. Phys. Rev. B 2013, 87, 155140. [Google Scholar] [CrossRef]
- Rizza, C.; Ciattoni, A.; Palange, E. Two-peaked and flat-top perfect bright solitons in nonlinear metamaterials with epsilon near zero. Phys. Rev. A 2011, 83, 053805. [Google Scholar] [CrossRef]
- Vincenti, M.A.; Kamandi, M.; de Ceglia, D.; Guclu, C.; Scalora, M.; Capolino, F. Second-harmonic generation in longitudinal epsilon-near-zero materials. Phys. Rev. B 2017, 96, 045438. [Google Scholar] [CrossRef]
- Wen, X.; Li, G.; Gu, C.; Zhao, J.; Wang, S.; Jiang, C.; Palomba, S.; de Sterke, C.M.; Xiong, Q. Doubly Enhanced Second Harmonic Generation through Structural and Epsilon-near-Zero Resonances in TiN Nanostructures. ACS Photonics 2018, 5, 2087–2093. [Google Scholar] [CrossRef]
- Alam, M.Z.; Schulz, S.A.; Upham, J.; De Leon, I.; Boyd, R.W. Large optical nonlinearity of nanoantennas coupled to an epsilon-near-zero material. Nat. Photonics 2018, 12, 79. [Google Scholar] [CrossRef]
- Ohashi, M.; Kondo, T.; Ito, R.; Fukatsu, S.; Shiraki, Y.; Kumata, K.; Kano, S.S. Determination of quadratic nonlinear optical coefficient of AlxGa1−xAs system by the method of reflected second harmonics. J. Appl. Phys. 1993, 74, 596–601. [Google Scholar] [CrossRef]
- Vabishchevich, P.P.; Liu, S.; Sinclair, M.B.; Keeler, G.A.; Peake, G.M.; Brener, I. Enhanced second-harmonic generation using broken symmetry III–V semiconductor fano metasurfaces. ACS Photonics 2018, 5, 1685–1690. [Google Scholar] [CrossRef]
- Timofeeva, M.; Lang, L.; Timpu, F.; Renaut, C.; Bouravleuv, A.; Shtrom, I.V.; Cirlin, G.; Grange, R. Anapoles in Free-Standing III-V Nanodisks Enhancing Second-Harmonic Generation. Nano Lett. 2018, 6, 3695–3702. [Google Scholar] [CrossRef] [PubMed]
- Gehrsitz, S.; Reinhart, F.K.; Gourgon, C.; Herres, N.; Vonlanthen, A.; Sigg, H. The refractive index of AlxGa1−xAs below the band gap: Accurate determination and empirical modeling. J. Appl. Phys. 2000, 87, 7825–7837. [Google Scholar] [CrossRef]
- Johnson, P.B.; Christy, R.W. Optical constants of the noble metals. Phys. Rev. B 1972, 6, 4370. [Google Scholar] [CrossRef]
- Hutter, T.; Huang, F.M.; Elliot, S.R.; Mahajan, S. Near-Field plasmonics of an individual dielectric nanoparticle above a metallic substrate. J. Phys. Chem. C 2013, 117, 7784–7790. [Google Scholar] [CrossRef]
- Grahn, P.; Shevchenko, A.; Kaivola, M. Electromagnetic multipole theory for optical nanomaterials. New J. Phys. 2012, 14, 093033. [Google Scholar] [CrossRef] [Green Version]
- Kim, J.; Dutta, A.; Naik, G.V.; Giles, A.J.; Bezares, F.J.; Ellis, C.T.; Tischler, J.G.; Mahmoud, A.M.; Caglayan, H.; Glembocki, O.J.; et al. Role of epsilon-near-zero substrates in the optical response of plasmonic antennas. Optica 2016, 3, 339–346. [Google Scholar] [CrossRef]
- Yang, Z.; Chak, P.; Bristow, A.D.; van Driel, H.M.; Iyer, R.; Aitchison, J.S.; Smirl, A.L.; Sipe, J.E. Enhanced second-harmonic generation in AlGaAs microring resonators. Opt. Lett. 2007, 32, 826–828. [Google Scholar] [CrossRef] [PubMed]




| Material | Re(ε) + j Im(ε) FW | Re(ε) + j Im(ε) SH |
|---|---|---|
| ENZ | −16.48 + j 0.4217 | 0.0006 + j 0.05 |
| Gold | −115.13 + j 11.259 | −22.068 + j 1.3708 |
| Dielectric | 2.56 + j 0 | 2.56 + j 0 |
| AlGaAs | 10.729 + j 0 | 12.583 + j 0.086 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rocco, D.; Vincenti, M.A.; De Angelis, C. Boosting Second Harmonic Radiation from AlGaAs Nanoantennas with Epsilon-Near-Zero Materials. Appl. Sci. 2018, 8, 2212. https://doi.org/10.3390/app8112212
Rocco D, Vincenti MA, De Angelis C. Boosting Second Harmonic Radiation from AlGaAs Nanoantennas with Epsilon-Near-Zero Materials. Applied Sciences. 2018; 8(11):2212. https://doi.org/10.3390/app8112212
Chicago/Turabian StyleRocco, Davide, Maria Antonietta Vincenti, and Costantino De Angelis. 2018. "Boosting Second Harmonic Radiation from AlGaAs Nanoantennas with Epsilon-Near-Zero Materials" Applied Sciences 8, no. 11: 2212. https://doi.org/10.3390/app8112212
APA StyleRocco, D., Vincenti, M. A., & De Angelis, C. (2018). Boosting Second Harmonic Radiation from AlGaAs Nanoantennas with Epsilon-Near-Zero Materials. Applied Sciences, 8(11), 2212. https://doi.org/10.3390/app8112212