Cracking Risk and Overall Stability Analysis of Xulong High Arch Dam: A Case Study
Abstract
:Featured Application
Abstract
1. Introduction
2. Summary of Cracking Types and Effect Factors of High Arch Dams
2.1. Cracking Types
2.2. Cracking Factors
- (1)
- Concrete materials. Different concrete materials have different properties such as hydration heat and tensile strength. High-strength concrete generally has a large content of cement, leading to high hydration heat. When the external temperature changes sharply or the temperature control measures are not appropriate, high-strength concrete can easily crack. Concrete materials should be selected according to different dam structures and high-strength concrete should not be used blindly.
- (2)
- Site selection of the arch dam. The complex geological conditions of the dam foundation directly affect the stress and deformation distribution of the arch dam. The uneven deformation of both abutments and different stiffness between arch dam and foundation can easily lead to arch dam cracking. Appropriate reinforcement methods are important for reducing the cracking risk of arch dams.
- (3)
- Temperature control and maintenance. Concrete temperature control measures are directly related to concrete thermal stress. The sharp increase or decrease of the external temperature has more influence on the dam abutment, heel, and outlets. The temperature control methods should be designed and implemented before the arch dam is built. For the special structures such as outlets, it is necessary to consider the cracking caused by the cavern drafts flowing and the outlets should be closed.
- (4)
- Dam profile design. Profile design needs to consider specific geological conditions. Arch dam profile is directly related to the stress distribution of the dam body. Outlets and dam heel should be considered especially. The effects of different profiles on the stress, deformation, overall stability, and cracking of the arch dam can be comprehensively compared by using the method of dividing load of the arch beam, FEM, and geomechanical model.
3. Numerical Modeling of the Xulong High Arch Dam
3.1. Numerical Method
3.2. Brief Introduction of Xulong Super-High Arch Dam
3.3. Numerical Model and Analysis Cases
4. Cracking Analysis of the Xulong High Arch Dam
4.1. Effect of Temperature Load on Stress and Displacement of the Xulong Arch Dam
4.2. Cracking Analysis of Dam Outlets
4.3. Cracking Analysis of the Dam Heel and the Dam Abutments
5. Overall Stability and Reinforcement Analysis of Xulong Arch Dam
5.1. Overall Stability Analysis
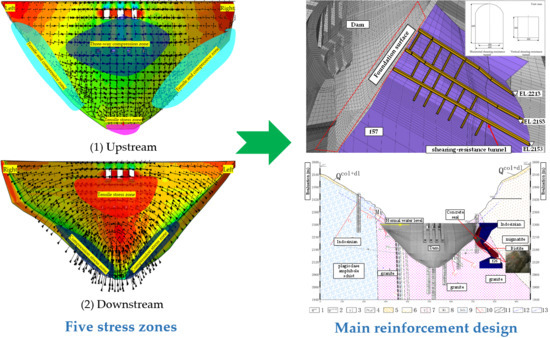
5.2. Discussion on Dam Stress Zones
5.3. Abutment Reinforcement Suggestion
6. Conclusions
- (1)
- A nonlinear constitutive model relating to the yielding region is proposed to evaluate dam cracking risk and overall stability. The temperature gradient change has a greater impact on the tensile stress and displacement of the arch dam, which increases dam cracking risk. In particular, the tensile stress of the left and right upper outlets are relatively large due to the pier.
- (2)
- The three safety factors of the Xulong arch dam are obtained, = 2~2.5; = 5; = 8.5, and the dam overall stability is guaranteed.
- (3)
- The five dam stress zones are proposed to analyze the dam cracking base of numerical results. It is recommended to use a shearing-resistance wall in the fault f57, replace the biotite enrichment zone with concrete, and perform consolidation grouting or anchoring on the excavated exposed weak structural zone. With optimal design of the dam structure according to the different stress characteristics of the five stress zones, the cracking risk and overall stability of the Xulong arch dam can be better controlled.
Author Contributions
Funding
Conflicts of Interest
References
- Lin, P.; Liu, X.-L.; Hu, S.-Y.; Li, P.-J. Large deformation analysis of a high steep slope relating to the Laxiwa reservoir, China. Rock Mech. Rock Eng. 2016, 49, 2253–2276. [Google Scholar] [CrossRef]
- Lin, P.; Zhou, W.-Y.; Liu, H.-Y. Experimental study on cracking, reinforcement, and overall stability of the Xiaowan super-high arch dam. Rock Mech. Rock Eng. 2015, 48, 819–841. [Google Scholar] [CrossRef]
- Lin, P.; Shi, J.; Zhou, W.-Y.; Wang, R.-K. 3D geomechanical model tests on asymmetric reinforcement and overall stability relating to the Jinping I super-high arch dam. Int. J. Rock Mech. Min. Sci. 2018, 102, 28–41. [Google Scholar] [CrossRef]
- Duffaut, P. The traps behind the failure of Malpasset arch dam, France, in 1959. J. Rock Mech. Geotech. Eng. 2013, 5, 335–341. [Google Scholar] [CrossRef]
- Lin, P.; Liu, H.-Y.; Li, Q.-B.; Hu, H. Effects of outlets on cracking risk and integral stability of super-high arch dams. Sci. World J. 2014, 2014, 312827. [Google Scholar] [CrossRef] [PubMed]
- Xia, S.-Y.; Lu, S.-W. Approach to cracking mechanism of Kolnbrein arch dam heel. Des. Hydroelectr. Power Stn. 1999, 15, 26–33. (In Chinese) [Google Scholar]
- Zhang, X.-F.; Wang, X.-P.; Huang, Y.; Li, S.-Y. Simulation study on temperature stress of RCC arch dam under cold wave conditions. J. Water Resour. Water Eng. 2018, 29, 192–197. (In Chinese) [Google Scholar] [CrossRef]
- Zhang, X.; Liu, X.-H.; Jing, X.-Y.; Wang, Q.; Chang, X.-L. Study on effect of thermal stress compensation for MgO concrete of high arch dam in cold area. Water Resour. Power 2013, 31, 82–85. (In Chinese) [Google Scholar]
- Mirzabozorg, H.; Hariri-Ardebili, M.A.; Shirkhan, M. Impact of solar radiation on the uncoupled transient thermo-structural response of an arch dam. Sci. Iran. 2015, 22, 1435–1448. [Google Scholar]
- Liang, R.-Q. Study of thermal control and crack prevention for high arch dam in dry-hot valley region. Yangtze River 2014, 45, 42–45. (In Chinese) [Google Scholar] [CrossRef]
- Sheibany, F.; Ghaemian, M. Effects of environmental action on thermal stress analysis of Karaj concrete arch dam. J. Eng. Mech. 2006, 132, 532–544. [Google Scholar] [CrossRef]
- Maken, D.D.; Léger, P.; Roth, S.N. Seasonal thermal cracking of concrete dams in northern regions. J. Perform. Constr. Facil. 2014, 28, 04014014. [Google Scholar] [CrossRef]
- Waleed, A.M.; Jaafar, M.S.; Noorzaei, J.; Bayagoob, K.H.; Amini, R. Effect of placement schedule on the thermal and structural response of RCC dams, using finite element analysis. In Proceedings of the Geo Jordan Conference 2004, Irbid, Jordan, 12–15 July 2004; pp. 94–104. [Google Scholar] [CrossRef]
- Jia, J.-S.; Li, X.-Y. Dam heel cracking problem in high arch dams and new measure for solution. J Hydraul. Eng. 2008, 39, 1183–1188. (In Chinese) [Google Scholar] [CrossRef]
- Lin, P.; Chen, X.; Zhou, W.-Y.; Yang, R.-Q.; Wang, R.-K. Simulation on back analysis of Shuanghe arch dam cracking. Rock Soil Mech. 2003, 24, 53–56. (In Chinese) [Google Scholar] [CrossRef]
- Câmara, R.J. A method for coupled arch dam-foundation-reservoir seismic behaviour analysis. Earthq. Eng. Struct. Dyn. 2000, 29, 441–460. [Google Scholar] [CrossRef]
- Lotfi, V.; Espandar, R. Seismic analysis of concrete arch dams by combined discrete crack and non-orthogonal smeared crack technique. Eng. Struct. 2004, 26, 27–37. [Google Scholar] [CrossRef]
- Hariri-Ardebili, M.A.; Seyed-Kolbadi, S.M. Seismic cracking and instability of concrete dams: Smeared crack approach. Eng. Fail. Anal. 2015, 52, 45–60. [Google Scholar] [CrossRef]
- Mi, Y.; Aliabadi, M.H. Dual boundary element method for three-dimensional fracture mechanics analysis. Eng. Anal. Bound. Elem. 1992, 10, 161–171. [Google Scholar] [CrossRef]
- Gerstle, W.H.; Ingraffea, A.R.; Perucchio, R. Three-dimensional fatigue crack propagation analysis using the boundary element method. Int. J. Fatigue 1988, 10, 187–192. [Google Scholar] [CrossRef]
- Lubliner, J.; Oliver, J.; Oller, S.; Onate, E. A plastic-damage model for concrete. Int. J. Solids Struct. 1989, 25, 299–326. [Google Scholar] [CrossRef]
- Lee, J.; Fenves, L.G. Plastic-damage model for cyclic loading of concrete structures. J. Eng. Mech. 1998, 124, 892–900. [Google Scholar] [CrossRef]
- Feng, L.M.; Pekau, O.A.; Zhang, C.H. Cracking analysis of arch dams by 3D boundary element method. J. Struct. Eng. 1996, 122, 691–699. [Google Scholar] [CrossRef]
- Chen, J.; Soltani, M.; An, X. Experimental and numerical study of cracking behavior of openings in concrete dams. Comput. Struct. 2005, 83, 525–535. [Google Scholar] [CrossRef]
- Sharan, S.K. Efficient finite element analysis of hydrodynamic pressure on dams. Comput. Struct. 1992, 42, 713–723. [Google Scholar] [CrossRef]
- Sato, H.; Miyazawa, S.; Yatagai, A. Thermal crack estimation of dam concrete considering the influence of autogenous shrinkage. In Proceedings of the 10th International Conference on Mechanics and Physics of Creep, Shrinkage, and Durability of Concrete and Concrete Structures (CONCREEP), Vienna, Austria, 21–23 September 2015; pp. 1289–1298. [Google Scholar] [CrossRef]
- Chow, W.-Y.; Yang, R.-Q. Determination of stability of arch dam abutment using finite element method and geomechanical models. In Proceedings of the 4th Australia—New Zealand Conference on Geomechanics, Perth, Australia, 14–18 May 1984; Volume 2, pp. 595–600. [Google Scholar]
- Zhou, W.-Y.; Yang, R.-Q.; Liu, Y.-R.; Lin, P. Research on geomechanical model of rupture tests of arch dams for their stability. J. Hydroelectr. Eng. 2005, 24, 53–58. (In Chinese) [Google Scholar] [CrossRef]
- Kou, X.-D.; Zhou, W.-Y. The application of element-free method to approximate calculation of arch dam crack propagation. J. Hydraul. Eng. 2000, 31, 28–35. (In Chinese) [Google Scholar]
- Portela, A.; Aliabadi, M.H.; Rooke, D.P. The dual boundary element method: Effective implementation for crack problems. Int. J. Numer. Methods Eng. 2010, 33, 1269–1287. [Google Scholar] [CrossRef]
- Singhal, A.C.; Nuss, L.K. Cable anchoring of deteriorated arch dam. J. Perform. Constr. Facil. 1991, 5, 19–36. [Google Scholar] [CrossRef]
- Hariri-Ardebili, M.A.; Saouma, V.E. Single and multi-hazard capacity functions for concrete dams. Soil Dyn. Earthq. Eng. 2017, 101, 234–249. [Google Scholar] [CrossRef]

















| Dam Name | Country | Operation Year | Height (m) | Cracking Description | Main Cracking Causes |
|---|---|---|---|---|---|
| Buffalo Bill Arch Dam | America | 1910 | 107.0 | Vertical cracks at downstream surface | Temperature (extreme thermal gradients) |
| Packard Sama Dam | America | 1928 | 113.0 | Different settlement | Earthquake |
| Stewart Mountain Dam [31] | America | 1930 | 64.6 | Visible surface, mainly upstream surface | Alkali–silica reactions and expansions |
| Zeuzier Dam | Switzerland | 1956 | 156.0 | Transverse joints open at upstream Peripheral joints form downstream | Foundation |
| Sardine Dam | Italy | 1957 | 115.0 | Horizontal cracks at upstream surface | Temperature |
| Santa Maria Dam | Switzerland | 1968 | 117.0 | Leakage in dam foundation upstream | Foundation |
| Daniel Johnson Dam [12] | Canada | 1968 | 214.0 | Oblique cracks at downstream surface | Seasonal temperature |
| Plunging cracks at the heel of the dam | Geometric discontinuities | ||||
| Kolnbrein Dam [6,14] | Austria | 1977 | 200.0 | Horizontal construction joints open Cracking at dam heel | Foundation |
| Zillergrundl Dam [14] | Austria | 1985 | 186 | Horizontal cracks at heelVertical cracks in the elevator shaft | Concrete hydration heat |
| Sayano-Shushenskaya Dam [14] | Former Soviet Union | 1989 | 242.0 | Vertical cracks in the gallery Horizontal cracks at upstream surface | Concrete hydration heat and temperature |
| Shuanghe Arch Dam [15] | China | 1991 | 82.3 | Seven vertical cracks at downstream surface | Self-weight and weak foundation |
| Ertan Dam | China | 2000 | 240.0 | Cracking at downstream surface | Foundation Temperature |
| Xiaowan Dam [2] | China | 2010 | 294.5 | Internal cracking | Temperature |
| Goupitan Dam | China | 2011 | 232.5 | Cracking around the bottom outlets | Concrete hydration heat and temperature |
| Materials | Bulk Density (t/m3) | Deformation Modulus (GPa) | Poisson’s Ratio | Shear Strength | |
|---|---|---|---|---|---|
| C′ (MPa) | F′ | ||||
| Dam concrete | 2.40 | 25.0 | 0.167 | 5.0 | 1.7 |
| Rock of type II | 2.70 | 24.0 | 0.22 | 1.2 | 1.1 |
| Rock of type III1 | 2.60 | 17.5 | 0.24 | 1.05 | 1.0 |
| Rock of type III2 | 2.55 | 12.5 | 0.26 | 1.0 | 0.95 |
| Rock of type IV | 2.50 | 6.0 | 0.30 | 0.65 | 0.60 |
| Normal Water Level + Temperature Rise | Normal Water Level + Temperature Drop | |||
|---|---|---|---|---|
| EL (m) | Mean Temperature Difference | Linear Temperature Difference | Mean Temperature Difference | Linear Temperature Difference |
| 2308 | 9.40 | 0.00 | 2.65 | 0.00 |
| 2302 | 7.67 | 3.09 | 3.22 | −0.49 |
| 2290 | 4.75 | 8.65 | 2.06 | 2.06 |
| 2270 | 2.42 | 12.54 | 0.68 | 5.67 |
| 2245 | 2.24 | 14.18 | 0.92 | 7.99 |
| 2220 | 2.79 | 14.66 | 1.67 | 8.98 |
| 2195 | 3.60 | 14.85 | 2.62 | 9.29 |
| 2170 | 3.58 | 14.72 | 2.65 | 9.45 |
| 2145 | 1.43 | 9.96 | 0.83 | 6.53 |
| 2120 | −0.97 | 4.74 | −1.35 | 2.60 |
| 2095 | −1.88 | 2.66 | −2.12 | 1.32 |
| Location | Content | Case 1 | Case 2 |
|---|---|---|---|
| Upstream surface | Maximum tensile stress of dam heel | 0.9 | 0.89 |
| Maximum tensile stress near left arch abutment | 1.18 | 1.17 | |
| Maximum tensile stress near right arch abutment | 0.97 | 0.94 | |
| Downstream surface | Maximum compression stress of dam toe | 6.93 | 7.35 |
| Maximum compression stress near left arch abutment | 8.76 | 8.88 | |
| Maximum compression stress near right arch abutment | 8.53 | 8.49 |
| Case 1 | Case 10 | |||||
|---|---|---|---|---|---|---|
| Left Arch Abutment | Arch Crown | Right Arch Abutment | Left Arch Abutment | Arch Crown | Right Arch Abutment | |
| Maximum (mm) | 6.55 | 32.9 | 5.04 | 8.29 | 20.2 | 5.98 |
| EL (m) | 2167.3 | 2308 | 2153 | 2167.3 | 2263 | 2153 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lin, P.; Wei, P.; Wang, W.; Huang, H. Cracking Risk and Overall Stability Analysis of Xulong High Arch Dam: A Case Study. Appl. Sci. 2018, 8, 2555. https://doi.org/10.3390/app8122555
Lin P, Wei P, Wang W, Huang H. Cracking Risk and Overall Stability Analysis of Xulong High Arch Dam: A Case Study. Applied Sciences. 2018; 8(12):2555. https://doi.org/10.3390/app8122555
Chicago/Turabian StyleLin, Peng, Pengcheng Wei, Weihao Wang, and Hongfei Huang. 2018. "Cracking Risk and Overall Stability Analysis of Xulong High Arch Dam: A Case Study" Applied Sciences 8, no. 12: 2555. https://doi.org/10.3390/app8122555
APA StyleLin, P., Wei, P., Wang, W., & Huang, H. (2018). Cracking Risk and Overall Stability Analysis of Xulong High Arch Dam: A Case Study. Applied Sciences, 8(12), 2555. https://doi.org/10.3390/app8122555