Symmetry-Breaking Effect on the Electromagnetic Properties of Plasmonic Trimers Composed of Graphene Nanodisks
Abstract
:1. Introduction
2. Simulation Method and Models
3. Results and Discussion
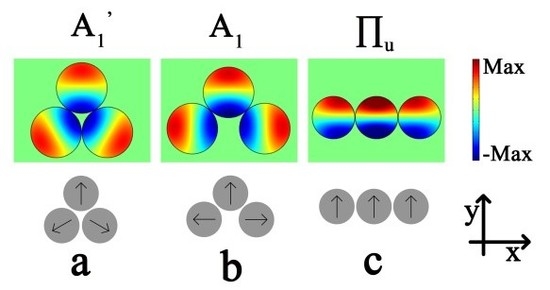
3.1. General Depiction of the Mode of Graphene Plasmonic Trimers
3.2. Energy Diagram of the Plasmonic Trimer
3.3. Quality Factor of Graphene Plasmonic Trimers
3.4. Scattering Properties of Graphene Plasmonic Trimers
3.5. Frequency Tunability of Graphene Plasmonic Trimers
3.6. Fabrication Process Suggestion
4. Summary
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Ku, J.F.; Chen, Q.D.; Ma, X.W.; Yang, Y.D.; Huang, Y.Z.; Xu, H.L.; Sun, H.B. Photonic-molecule single-mode laser. IEEE Photonics Technol. Lett. 2015, 27, 1157–1160. [Google Scholar] [CrossRef]
- Kudryashov, A.V.; Boriskina, S.V.; Paxton, A.H.; Benson, T.M.; Sewell, P.; Ilchenko, V.S. Photonic molecules made of matched and mismatched microcavities: New functionalities of microlasers and optoelectronic components. Proc. SPIE 2007, 6452, 64520X. [Google Scholar] [CrossRef]
- Vahala, K.J. Optical microcavities. Nature 2003, 424, 839–846. [Google Scholar] [CrossRef] [PubMed]
- Chuntonov, L.; Haran, G. Trimeric plasmonic molecules: The role of symmetry. Nano Lett. 2011, 11, 2440–2445. [Google Scholar] [CrossRef] [PubMed]
- Wang, H.; Brandl, D.W.; Nordlander, P.; Halas, N.J. Plasmonic nanostructures artificial molecules. Acc. Chem. Res. 2007, 40, 53–62. [Google Scholar] [CrossRef] [PubMed]
- Mukherjee, S.; Sobhani, H.; Lassiter, J.B.; Bardhan, R.; Nordlander, P.; Halas, N.J. Fanoshells: Nanoparticles with built-in fano resonances. Nano Lett. 2010, 10, 2694–2701. [Google Scholar] [CrossRef] [PubMed]
- Luk’yanchuk, B.; Zheludev, N.I.; Maier, S.A.; Halas, N.J.; Nordlander, P.; Giessen, H.; Chong, C.T. The Fano resonance in plasmonic nanostructures and metamaterials. Nat. Mater. 2010, 9, 707–715. [Google Scholar] [CrossRef] [PubMed]
- Hentschel, M.; Saliba, M.; Vogelgesang, R.; Giessen, H.; Alivisatos, A.P.; Liu, N. Transition from isolated to collective modes in plasmonic oligomers. Nano Lett. 2010, 10, 2721–2726. [Google Scholar] [CrossRef] [PubMed]
- Papasimakis, N.; Fedotov, V.A.; Zheludev, N.I.; Prosvirnin, S.L. Metamaterial analog of electromagnetically induced transparency. Phys. Rev. Lett. 2008, 101, 253903. [Google Scholar] [CrossRef] [PubMed]
- Liu, N.; Langguth, L.; Weiss, T.; Kastel, J.; Fleischhauer, M.; Pfau, T.; Giessen, H. Plasmonic analogue of electromagnetically induced transparency at the drude damping limit. Nat. Mater. 2009, 8, 758–762. [Google Scholar] [CrossRef] [PubMed]
- Willets, K.A.; Van Duyne, R.P. Localized surface plasmon resonance spectroscopy and sensing. Annu. Rev. Phys. Chem. 2007, 58, 267–297. [Google Scholar] [CrossRef] [PubMed]
- Chuntonov, L.; Haran, G. Optical activity in single-molecule surface-enhanced raman scattering: Role of symmetry. MRS Bull. 2013, 38, 642–647. [Google Scholar] [CrossRef]
- Chuntonov, L.; Haran, G. Effect of symmetry breaking on the mode structure of trimeric plasmonic molecules. J. Phys. Chem. C 2011, 115, 19488–19495. [Google Scholar] [CrossRef]
- Verre, R.; Yang, Z.J.; Shegai, T.; Kall, M. Optical magnetism and plasmonic Fano resonances in metal-insulator-metal oligomers. Nano Lett. 2015, 15, 1952–1958. [Google Scholar] [CrossRef] [PubMed]
- Fan, J.A.; Wu, C.; Bao, K.; Bao, J.; Bardhan, R.; Halas, N.J.; Manoharan, V.N.; Nordlander, P.; Shvets, G.; Capasso, F. Self-assembled plasmonic nanoparticle clusters. Science 2010, 328, 1135–1138. [Google Scholar] [CrossRef] [PubMed]
- Zhao, J.; Qiu, W.; Huang, Y.; Wang, J.X.; Kan, Q.; Pan, J.Q. Investigation of plasmonic whispering-gallery mode characteristics for graphene monolayer coated dielectric nanodisks. Opt. Lett. 2014, 39, 5527–5530. [Google Scholar] [CrossRef] [PubMed]
- Qiu, W.; Liu, X.; Zhao, J.; He, S.; Ma, Y.; Wang, J.-X.; Pan, J. Nanofocusing of mid-infrared electromagnetic waves on graphene monolayer. Appl. Phys. Lett. 2014, 104, 041109. [Google Scholar] [CrossRef]
- Zhang, H.; Virally, S.; Bao, Q.; Ping, L.; Massar, S.; Godbout, N.; Kockaert, P. Z-scan measurement of the nonlinear refractive. Opt. Lett. 2012, 37, 1856–1858. [Google Scholar] [CrossRef] [PubMed]
- Li, Z.Q.; Henriksen, E.A.; Jiang, Z.; Hao, Z.; Martin, M.C.; Kim, P.; Stormer, H.L.; Basov, D.N. Dirac charge dynamics in graphene by infrared spectroscopy. Nat. Phys. 2008, 4, 532–535. [Google Scholar] [CrossRef]
- Novoselov, K.S.; Geim, A.K.; Morozov, S.V.; Jiang, D.; Katsnelson, M.I.; Grigorieva, I.V.; Dubonos, S.V.; Firsov, A.A. Two-dimensional gas of massless Dirac fermions in graphene. Nature 2005, 438, 197–200. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ren, J.; Qiu, W.; Chen, H.; Qiu, P.; Lin, Z.; Wang, J.X.; Kan, Q.; Pan, J.Q. Electromagnetic field coupling characteristics in graphene plasmonic oligomers: From isolated to collective modes. Phys. Chem. Chem. Phys. 2017, 19, 14671–14679. [Google Scholar] [CrossRef] [PubMed]
- Hwang, E.H.; Das Sarma, S. Dielectric function, screening, and plasmons in two-dimensional graphene. Phys. Rev. B 2007, 75, 205418. [Google Scholar] [CrossRef]
- Liu, M.; Yin, X.; Ulin-Avila, E.; Geng, B.; Zentgraf, T.; Ju, L.; Wang, F.; Zhang, X. A graphene-based broadband optical modulator. Nature 2011, 474, 64–67. [Google Scholar] [CrossRef] [PubMed]
- Mittendorff, M.; Li, S.S.; Murphy, T.E. Graphene-based waveguide-integrated terahertz modulator. ACS Photonics 2017, 4, 316–321. [Google Scholar] [CrossRef]
- Correas-Serrano, D.; Gomez-Diaz, J.S.; Alu, A.; Melcon, A.A. Electrically and magnetically biased graphene-based cylindrical waveguides: Analysis and applications as reconfigurable antennas. IEEE Trans. Terahertz Sci. Technol. 2015, 5, 951–960. [Google Scholar] [CrossRef]
- Sensale-Rodriguez, B.; Yan, R.; Zhu, M.; Jena, D.; Liu, L.; Grace Xing, H. Efficient terahertz electro-absorption modulation employing graphene plasmonic structures. Appl. Phys. Lett. 2012, 101, 261115. [Google Scholar] [CrossRef]
- Qiu, P.; Qiu, W.; Lin, Z.; Chen, H.; Tang, Y.; Wang, J.X.; Kan, Q.; Pan, J.Q. Investigation of the band structure of graphene-based plasmonic photonic crystals. Nanomaterials 2016, 6, 166. [Google Scholar] [CrossRef] [PubMed]
- Hanson, G.W. Dyadic green’s functions and guided surface waves for a surface conductivity model of graphene. J. Appl. Phys. 2008, 103, 064302. [Google Scholar] [CrossRef]
- Amanatiadis, S.A.; Kantartzis, N.V.; Tsiboukis, T.D. A loss-controllable absorbing boundary condition for surface plasmon polaritons propagating onto graphene. IEEE Trans. Magn. 2015, 51, 4. [Google Scholar] [CrossRef]
- Papadimopoulos, A.N.; Amanatiadis, S.A.; Kantartzis, N.V.; Rekanos, I.T.; Zygiridis, T.T.; Tsiboukis, T.D. A convolutional PML scheme for the efficient modeling of graphene structures through the ADE-FDTD technique. IEEE Trans. Magn. 2017, 53, 1–4. [Google Scholar] [CrossRef]
- Zhao, J.; Liu, X.; Qiu, W.; Ma, Y.; Huang, Y.; Wang, J.X.; Qiang, K.; Pan, J.Q. Surface-plasmon-polariton whispering-gallery mode analysis of the graphene monolayer coated ingaas nanowire cavity. Opt. Express 2014, 22, 5754–5761. [Google Scholar] [CrossRef] [PubMed]
- Chen, J.; Badioli, M.; Alonso-Gonzalez, P.; Thongrattanasiri, S.; Huth, F.; Osmond, J.; Spasenovic, M.; Centeno, A.; Pesquera, A.; Godignon, P.; et al. Optical nano-imaging of gate-tunable graphene plasmons. Nature 2012, 487, 77–81. [Google Scholar] [CrossRef] [PubMed]
- Kim, M.W.; Ku, P.C. Lasing in a metal-clad microring resonator. Appl. Phys. Lett. 2011, 98, 131107. [Google Scholar] [CrossRef]
- Ju, L.; Geng, B.; Horng, J.; Girit, C.; Martin, M.; Hao, Z.; Bechtel, H.A.; Liang, X.; Zettl, A.; Shen, Y.R.; et al. Graphene plasmonics for tunable terahertz metamaterials. Nat. Nanotechnol. 2011, 6, 630–634. [Google Scholar] [CrossRef] [PubMed]
- Ren, J.B.; Wang, G.Q.; Qiu, W.B.; Lin, Z.L.; Chen, H.B.; Qiu, P.P.; Wang, J.X.; Kan, Q.; Pan, J.Q. Optimization of the Fano resonance lineshape based on graphene plasmonic hexamer in mid-infrared frequencies. Nanomaterials 2017, 7, 238. [Google Scholar] [CrossRef] [PubMed]
- Amanatiadis, S.; Kantartzis, N. Distortion of surface plasmon polariton propagation on graphene due to chemical potential variation. Appl. Phys. A 2016, 122, 313. [Google Scholar] [CrossRef]
- Low, T.; Avouris, P. Graphene plasmonics for terahertz to mid-infrared applications. ACS Nano 2014, 8, 1086–1101. [Google Scholar] [CrossRef] [PubMed]
- Chen, H.B.; Qiu, W.B.; Qiu, P.P.; Ren, J.B.; Lin, Z.L.; Wang, J.X.; Kan, Q.; Pan, J.Q. Mode coupling properties of the plasmonic dimers composed of graphene nanodisks. Appl. Sci. 2017, 7, 359. [Google Scholar] [CrossRef]
- Qiu, W.; Huang, Y.; Chen, H.; Qiu, P.; Tang, Y.; Wang, J.-X.; Kan, Q.; Pan, J.-Q. Coupling of whispering-gallery modes in the graphene nanodisk plasmonic dimers. Plasmonics 2016, 12, 39–45. [Google Scholar] [CrossRef]
- Lu, W.B.; Zhu, W.; Xu, H.J.; Ni, Z.H.; Dong, Z.G.; Cui, T.J. Flexible transformation plasmonics using graphene. Opt. Express 2013, 21, 10475–10482. [Google Scholar] [CrossRef] [PubMed]
- Vakil, A.; Engheta, N. Transformation optics using graphene. Science 2011, 332, 1291–1294. [Google Scholar] [CrossRef] [PubMed]
- Wang, B.; Zhang, X.; Yuan, X.C.; Teng, J.H. Optical coupling of surface plasmons between graphene sheets. Appl. Phys. Lett. 2012, 100, 4. [Google Scholar] [CrossRef]
- Gusynin, V.P.; Sharapov, S.G.; Carbotte, J.P. Magneto-optical conductivity in graphene. J. Phys. Condens. Matter 2007, 19, 25. [Google Scholar] [CrossRef]
- Huang, Y.; Qiu, W.; Lin, S.; Zhao, J.; Chen, H.; Wang, J.-X.; Kan, Q.; Pan, J.-Q. Investigation of plasmonic whispering gallery modes of graphene equilateral triangle nanocavities. Sci. China Inf. Sci. 2016, 59, 042413. [Google Scholar] [CrossRef]








© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qiu, W.; Chen, H.; Ren, J.; Qiu, P.; Lin, Z.; Wang, J.; Kan, Q.; Pan, J. Symmetry-Breaking Effect on the Electromagnetic Properties of Plasmonic Trimers Composed of Graphene Nanodisks. Appl. Sci. 2018, 8, 374. https://doi.org/10.3390/app8030374
Qiu W, Chen H, Ren J, Qiu P, Lin Z, Wang J, Kan Q, Pan J. Symmetry-Breaking Effect on the Electromagnetic Properties of Plasmonic Trimers Composed of Graphene Nanodisks. Applied Sciences. 2018; 8(3):374. https://doi.org/10.3390/app8030374
Chicago/Turabian StyleQiu, Weibin, Houbo Chen, Junbo Ren, Pingping Qiu, Zhili Lin, Jiaxian Wang, Qiang Kan, and Jiaoqing Pan. 2018. "Symmetry-Breaking Effect on the Electromagnetic Properties of Plasmonic Trimers Composed of Graphene Nanodisks" Applied Sciences 8, no. 3: 374. https://doi.org/10.3390/app8030374
APA StyleQiu, W., Chen, H., Ren, J., Qiu, P., Lin, Z., Wang, J., Kan, Q., & Pan, J. (2018). Symmetry-Breaking Effect on the Electromagnetic Properties of Plasmonic Trimers Composed of Graphene Nanodisks. Applied Sciences, 8(3), 374. https://doi.org/10.3390/app8030374