The Rotating Flow of Magneto Hydrodynamic Carbon Nanotubes over a Stretching Sheet with the Impact of Non-Linear Thermal Radiation and Heat Generation/Absorption
Abstract
:1. Introduction
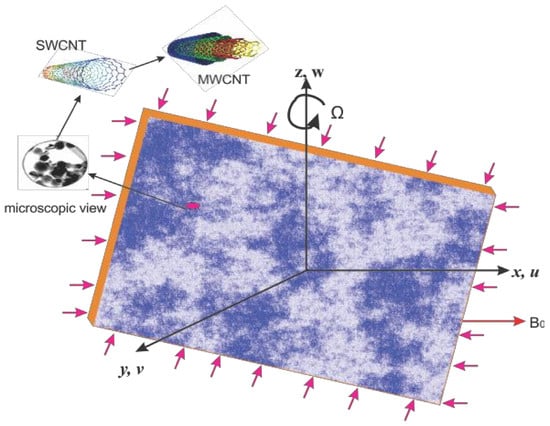
2. Problem Formulation
3. Physical Quantities of Interest
4. Solution Methodology
4.1. Zeroth Order Deformation of the Problem
4.2. ith-Order Deformation Problem
5. HAM Scheme Convergence
6. Results and Discussion
Table Discussion
7. Conclusions
- For CNTs, large values of (the rotation parameter) produce smaller velocities and , but the opposite tendency is detected for temperature profile .
- Increasing the nanoparticle volume fraction into the working liquid boosted , and values for SWCNTs and MWCNTs.
- A strong magnetic parameter reduces and , while increases the temperature .
- The thermal layer rises through heat generation for SWCNTs and MWCNTs.
- The large values of Prandlt number , reduces nanoparticle temperature .
- Large values of Biot number boost temperature and thicken the boundary film concentration.
- The degree of coefficient of skin friction increases for larger values. The results show that skin friction in case of SWCNTs is higher than in MWCNTs.
- Heat transfer rate is controlled by large values of and
- Nusselt number is greater with SWCNTs as opposed to MWCNTs.
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Dai, L.; Chang, D.W.; Baek, J.B.; Lu, W. Carbon nanomaterials for advanced energy conversion and storage. Small 2012, 8, 1130–1166. [Google Scholar] [PubMed]
- Iijima, S. Helical microtubules of graphitic carbon. Nature 1991, 354, 56–58. [Google Scholar] [CrossRef]
- Ajayan, P.M.; Iijima, S. Capillarity-induced filling of carbon nanotubes. Nature 1993, 361, 333–334. [Google Scholar] [CrossRef]
- Choi, S.U.S. Enhancing Thermal Conductivity of Fluids with Nanoparticles, Developments and Applications of Non-Newtonian Flows; Siginer, D.A., Wang, H.P., Eds.; American Society of Mechanical Engineers (ASME): New York, NY, USA, 1995; Volume 231, pp. 99–105. [Google Scholar]
- Said, Z.; Saidur, R.; Rahim, N.A.; Alim, M.A. Analyses of energy efficiency and pumping power for a conventional flat plate solar collector using SWCNTs based nanofluid. Energy Build. 2014, 78, 1–9. [Google Scholar] [CrossRef]
- Xiao, J.; Pan, X.; Guo, S.; Ren, P.; Bao, X. Toward fundamentals of confined catalysis in carbon nanotube. J. Am. Chem. Soc. 2015, 137, 477–480. [Google Scholar] [CrossRef] [PubMed]
- Halelfadi, S.; Mare, T.; Estelle, P. Efficiency of carbon nanotubes water based nanofluids as coolants. Exp. Therm. Fluid Sci. 2014, 53, 104–110. [Google Scholar] [CrossRef] [Green Version]
- Aman, S.; Khan, I.; Ismail, Z.; Salleh, M.Z.; Alshomrani, A.S.; Alghamdi, M.S. Magnetic field effect on Poiseuille flow and heat transfer of carbon nanotubes along a vertical channel filled with Casson fluid Citation. AIP Adv. 2017, 7, 015036. [Google Scholar] [CrossRef]
- Hayat, T.; Hussain, Z.; Alsaedi, A.; Asghar, S. Carbon nanotubes effects in the stagnation point flow towards a nonlinear stretching sheet with variable thickness. Adv. Powder Technol. 2016, 27, 1677–1688. [Google Scholar] [CrossRef]
- Wen, D.; Ding, Y. Effective thermal conductivity of aqueous suspensions of carbon nanotubes. J. Thermophys. Heat Transf. 2004, 18, 481–485. [Google Scholar] [CrossRef]
- Mayer, J.; Mckrell, T.; Grote, K. The influence of multi-walled carbon nanotubes on single-phase heat transfer and pressure drop characteristics in the transitional flow regime of smooth tubes. Int. J. Heat Mass Transf. 2013, 58, 597–609. [Google Scholar] [CrossRef]
- Kamli, R.; Binesh, A. Numerical investigation of heat transfer enhancement using carbon nanotube-based non-newtonian nanofluids. Int. Commun. Heat Mass Transf. 2010, 37, 1153–1157. [Google Scholar] [CrossRef]
- Hussain, S.T.; Haq, R.U.; Khan, Z.H.; Nadeem, S. Water driven flow of carbon nanotubes in a rotating channel. J. Mol. Liq. 2016, 214, 136–144. [Google Scholar] [CrossRef]
- Aman, S.; Khan, I.; Ismail, Z.; Salleh, M.Z.; Al-Mdallal, Q.M. Heat transfer enhancement in free convection flow of CNTs Maxwell nanofluids with four different types of molecular liquids. Sci. Rep. 2017, 7, 1–13. [Google Scholar] [CrossRef] [PubMed]
- Hayat, T.; Haider, F.; Muhammad, T.; Alsaedi, A. Three Dimensional rotating flow of carbon nanotubes with Darcy-Frochheimer porous medium. PLoS ONE 2017, 12, e0179576. [Google Scholar] [CrossRef] [PubMed]
- Manevitch, L.I.; Smirnov, V.V.; Strozzi, M.; Pellicano, F. Nonlinear optical vibrations of single-walled carbon nanotubes. Int. J. Nonlinear Mech. 2017, 94, 351–361. [Google Scholar] [CrossRef]
- Imtiaz, M.; Hayat, T.; Alsaedi, A.; Ahmad, B. Convective flow of carbon nanotubes between rotating stretchable disks with thermal radiation effects. Int. J. Heat Mass Transf. 2016, 101, 948–957. [Google Scholar] [CrossRef]
- Tran, T.Q.; Headrick, R.J.; Bengio, E.A.; Myint, S.M.; Khoshnevis, H.; Jamali, V.; Duong, H.M.; Pasquali, M. Purification and Dissolution of carbon nanotube fiber SPUM from floating catalyst method. ACS Appl. Mater. Interfaces 2017, 9, 37112–37119. [Google Scholar] [CrossRef] [PubMed]
- Casson, N. A Flow Equation for Pigment Oil Suspensions of the Printing Ink Type, Rheology of Disperse Systems; Pergamon Press: New York, NY, USA, 1959; pp. 84–104. [Google Scholar]
- Dash, R.K.; Mehta, K.N.; Jayaraman, G. Effect of yield stress on the flow of a Casson fluid in a homogeneous porous medium bounded by a circular tube. Appl. Sci. Res. 1996, 57, 133–149. [Google Scholar] [CrossRef]
- Pramanik, S. Casson fluid flow and heat transfer past an exponentially porous stretching surface in presence of thermal radiation. Ain Shams Eng. J. 2014, 5, 205–212. [Google Scholar] [CrossRef]
- Hussanan, A.; Salleh, M.Z.; Tahar, R.M.; Khan, I. Unsteady boundary layer flow and heat transfer of a Casson fluid past an oscillating vertical plate with Newtonian heating. PLoS ONE 2014, 9, e108763. [Google Scholar] [CrossRef] [PubMed]
- Asma, K.; Khan, I.; Arshad, K.; Sharidan, S. Unsteady MHD free convection flow of Casson fluid past over an oscillatin vertical plate embedded in a porous medium. Eng. Sci. Technol. Int. J. 2015, 18, 309–317. [Google Scholar]
- Walicka, A.; Falicki, J. Reynolds number effects in the flow of an electro rheological fluid of Casson type between fixed surface of revolution. Appl. Math. Comput. 2015, 250, 639–649. [Google Scholar]
- Nadeem, S.; Haq, R.U.; Noreen, A.S. MHD three-dimensional boundary layer flow of Casson nanofluid past a linearly stretching sheet with convective boundary condition. IEEE Trans. Nanotechnol. 2014, 13, 109–115. [Google Scholar] [CrossRef]
- Mukhopadhyay, S.; Bhattacharyya, K.; Hayat, T. Exact solutions for the flow of Casson fluid over a stretching surface with transpiration and heat transfer effects. Chin. Phys. B 2013, 22, 114701. [Google Scholar] [CrossRef]
- Mukhopadhyay, S.; Mandal, I.S. Boundary layer flow and heat transfer of a Casson fluid past a symmetric porous wedge with surface heat flux. Chin. Phys. B 2014, 23, 044702. [Google Scholar] [CrossRef]
- Ariel Hiemenz, P.D. Flow in hydro magnetics. Acta Mech. 1994, 103, 31–43. [Google Scholar]
- Ganapathirao, M.; Ravindran, R. Non-uniform slot suction/injection into mixed convective MHD flow over a vertical wedge with chemical reaction. Procedia Eng. 2015, 127, 1102–1109. [Google Scholar] [CrossRef]
- Rahman, M.M.; Al-Lawatia, M.A.; Eltayeb, I.A.; Al-Salti, N. Hydromagnetic slip flow of water based nanofluids past a wedge with convective surface in the presence of heat generation (or) absorption. Int. J. Therm. Sci. 2012, 57, 172–182. [Google Scholar] [CrossRef]
- Srinivasacharya, D.; Mendu, U.; Venumadhav, K. MHD boundary layer flow of a nanofluid past a wedge. Procedia Eng. 2015, 127, 1064–1070. [Google Scholar] [CrossRef]
- Hammed, H.; Haneef, M.; Shah, Z.; Islam, S.; Khan, W.; Muhammad, S. The Combined Magneto hydrodynamic and electric field effect on an unsteady Maxwell nanofluid Flow over a Stretching Surface under the Influence of Variable Heat and Thermal Radiation. Appl. Sci. 2018, 8, 160. [Google Scholar] [CrossRef]
- Shah, Z.; Gul, T.; Khan, A.M.; Ali, I.; Islam, S. Effects of hall current on steady three dimensional non-newtonian nanofluid in a rotating frame with brownian motion and thermophoresis effects. J. Eng. Technol. 2017, 6, 280–296. [Google Scholar]
- Shah, Z.; Islam, S.; Gul, T.; Bonyah, E.; Khan, M.A. The electrical MHD and hall current impact on micropolar nanofluid flow between rotating parallel plates. Results Phys. 2018. [Google Scholar] [CrossRef]
- Crane, L.J. Flow past a stretching plate. Z. Angew. Math. Phys. 1970, 21, 645–647. [Google Scholar] [CrossRef]
- Vajravelu, K.; Roper, T. Flow and heat transfer in a second grade fluid over a stretching sheet. Int. J. Nonlinear Mech. 1999, 34, 1031–1036. [Google Scholar] [CrossRef]
- Rosca, N.C.; Pop, I. Unsteady boundary layer OW over a permeable curved stretching/shrinking surface. Eur. J. Mech. B 2015, 51, 61–67. [Google Scholar] [CrossRef]
- Sajid, M.; Ali, N.; Javed, T.; Abbas, Z. Stretching a curved surface in a viscous fluid. Chin. Phys. Lett. 2010, 27, 024703. [Google Scholar] [CrossRef]
- Khan, W.A.; Pop, I. Boundary-Layer Flow of a Nanouid Past a Stretching Sheet. Int. J. Heat Mass Transf. 2010, 53, 2477–2483. [Google Scholar] [CrossRef]
- Hassani, M.; Tabar, M.M.; Nemati, H.; Domairry, G.; Noori, F. An analytical solution for boundary layer flow of a Nano liquid past a stretching sheet. Int. J. Therm. Sci. 2011, 50, 2256–2263. [Google Scholar] [CrossRef]
- Pooya, M.; Rad, C. The Effect of Thermal Radiation on Nanouid Cooled Microchannels. J. Fusion Energy 2009, 28, 91–100. [Google Scholar]
- Afify, A.; Seddeek, M.A.; Bbazid, M.A.A. Radiation effects on Falkner-Skan flow of a nanouid past a wedge in the present of non-uniform heat source/sink. Meccanica 2011. submitted. [Google Scholar]
- Brinkman, H.C. The viscosity of concentrated suspensions and solution. J. Chem. Phys. 1952, 20, 571–581. [Google Scholar] [CrossRef]
- Xue, Q. Model for thermal conductivity of carbon nanotube-based composites. Phys. B Condens. Matter 2005, 368, 302–307. [Google Scholar] [CrossRef]
- Liao, S.J. On the homotopy analysis method for nonlinear problems. Appl. Math. Comput. 2007, 147, 499–513. [Google Scholar] [CrossRef]
- Liao, S.J. Comparison between the homotopy analysis method and homotopy perturbation method. Appl. Math. Comput. 2005, 169, 1186–1194. [Google Scholar] [CrossRef]
- Abbasbandy, S. The application of homotopy analysis method to solve a generalized Hirota-Satsuma Coupled KdV equation. Phys. Lett. A 2007, 361, 478–483. [Google Scholar] [CrossRef]
- Zhen, W.; Li, Z.; Qing, Z.H. Solitary solution of discrete mKdV equation by homotopy analysis method. Commun. Theor. Phys. 2008, 49, 1373–1378. [Google Scholar] [CrossRef]














| Physical Properties | Density | Thermal Conduct | Specific Heat | |
|---|---|---|---|---|
| Base fluid | Water | 997 | 0.613 | 4197 |
| Kerosene (lamp) oil | 783 | 0.145 | 2090 | |
| Engine oil | 884 | 0.144 | 1910 | |
| Nanoparticles | SWCNT | 2600 | 6600 | 425 |
| MWCNT | 1600 | 3000 | 796 | |
| Volume Fraction | Thermal Conductivity for SWCNT | Thermal Conductivity for MWCNT |
|---|---|---|
| 0 | 0.145 | 0.145 |
| 0.01 | 0.174 | 0.172 |
| 0.02 | 0.204 | 0.2 |
| 0.03 | 0.235 | 0.228 |
| 0.04 | 0.266 | 0.257 |
| SWCNT | MWCNT | SWCNT | MWCNT | ||||
|---|---|---|---|---|---|---|---|
| 0.0 | 0.1 | 0.1 | 0.1 | 1.03456 | 1.14526 | ||
| 0.1 | 1.12677 | 1.19870 | |||||
| 0.3 | 1.14340 | 1.24358 | |||||
| 0.1 | 0.0 | 1.04566 | 1.13657 | ||||
| 0.3 | 0.23561 | 1.17452 | |||||
| 0.5 | 0.02537 | 1.32435 | |||||
| 0.1 | 0.0 | 0.23409 | 1.03452 | ||||
| 0.3 | 1.45473 | 1.10034 | |||||
| 0.5 | 1.52435 | 1.37342 | |||||
| 0.1 | 0.1 | 1.69211 | 1.57235 | 1.72340 | 1.22349 | ||
| 0.3 | 1.62345 | 1.31902 | |||||
| 0.5 | 1.92345 | 1.81189 | 1.90823 | 1.59321 | |||
| SWCNT | MWCNT | |||||
|---|---|---|---|---|---|---|
| 0.0 | 0.1 | 0.1 | 0.1 | 0.1 | 0.231567 | |
| 0.1 | 0.232390 | |||||
| 0.3 | 0.233321 | |||||
| 0.1 | 0.0 | 0.134136 | ||||
| 0.3 | 0.134342 | |||||
| 0.5 | 0.134351 | |||||
| 0.1 | 0.3 | 0.261532 | ||||
| 0.5 | 0.261531 | |||||
| 0.8 | 0.261530 | |||||
| 0.1 | 0.5 | 0.156382 | ||||
| 1.0 | 0.234521 | |||||
| 1.5 | 0.267373 | |||||
| 0.1 | 0.5 | 0.234536 | ||||
| 1.0 | 0.198342 | |||||
| 1.5 | 0.162435 | |||||
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Muhammad, S.; Ali, G.; Shah, Z.; Islam, S.; Hussain, S.A. The Rotating Flow of Magneto Hydrodynamic Carbon Nanotubes over a Stretching Sheet with the Impact of Non-Linear Thermal Radiation and Heat Generation/Absorption. Appl. Sci. 2018, 8, 482. https://doi.org/10.3390/app8040482
Muhammad S, Ali G, Shah Z, Islam S, Hussain SA. The Rotating Flow of Magneto Hydrodynamic Carbon Nanotubes over a Stretching Sheet with the Impact of Non-Linear Thermal Radiation and Heat Generation/Absorption. Applied Sciences. 2018; 8(4):482. https://doi.org/10.3390/app8040482
Chicago/Turabian StyleMuhammad, Sher, Gohar Ali, Zahir Shah, Saeed Islam, and Syed Asif Hussain. 2018. "The Rotating Flow of Magneto Hydrodynamic Carbon Nanotubes over a Stretching Sheet with the Impact of Non-Linear Thermal Radiation and Heat Generation/Absorption" Applied Sciences 8, no. 4: 482. https://doi.org/10.3390/app8040482
APA StyleMuhammad, S., Ali, G., Shah, Z., Islam, S., & Hussain, S. A. (2018). The Rotating Flow of Magneto Hydrodynamic Carbon Nanotubes over a Stretching Sheet with the Impact of Non-Linear Thermal Radiation and Heat Generation/Absorption. Applied Sciences, 8(4), 482. https://doi.org/10.3390/app8040482