Detection and Quantification of Damage in Metallic Structures by Laser-Generated Ultrasonics
Abstract
:1. Introduction
2. Background
2.1. Generation and Modulation of Laser-Generated Ultrasonics
2.2. Reconstruction of the State-Space Attractor
2.3. Feature Extraction
2.4. Damage Detection and Quantification
3. Experimental Setup and Testing Structures
3.1. Laser-Generated Ultrasonics Damage Detection System
3.2. Testing Structures
4. Artificial Damage Detection and Quantification for Aluminum Alloy Plates
4.1. Ultrasonic Responses in Time Domain
4.2. Calculation of Embedding Parameters
4.3. Damage-Sensitive Feature: NNPE
4.4. Damage Visualization and Quantification
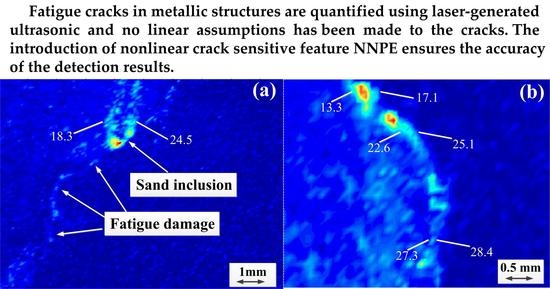
5. Actual Damage Detection and Quantification of a Twin-Screw Compressor Body
5.1. Description of the Detection of a Twin-Screw Compressor Body
5.2. Damage Visualization and Quantification
6. Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Chatterjee, A.; Kotambkar, M.S. Modal characteristics of turbine blade packets under lacing wire damage induced mistuning. J. Sound Vib. 2015, 343, 49–70. [Google Scholar] [CrossRef]
- Ukar, E.; Lamikiz, A.; Martínez, S.; Tabernero, I.; López De Lacalle, L.N. Roughness prediction on laser polished surfaces. J. Mater. Process. Technol. 2012, 212, 1305–1313. [Google Scholar] [CrossRef]
- Suárez, A.; Veiga, F.; López De Lacalle, L.N.; Polvorosa, R.; Lutze, S.; Wretland, A. Effects of ultrasonics-assisted face milling on surface integrity and fatigue life of Ni-Alloy 718. J. Mater. Eng. Perform. 2016, 25, 5076–5086. [Google Scholar]
- Campbell, F.C. Elements of Metallurgy and Engineering Alloys; ASM International: Novelty, OH, USA, 2008. [Google Scholar]
- Lee, C.; Kim, J.; Park, S.; Kim, D.H. Advanced fatigue crack detection using nonlinear self-sensing impedance technique for automated NDE of metallic structures. Res. Nondestruct. Eval. 2015, 26, 107–121. [Google Scholar] [CrossRef]
- Calleja Ochoa, A.; González Barrio, H.; Polvorosa Teijeiro, R.; Ortega Rodríguez, N.; López-de-Lacalle, L.N. Multitasking machines: Evolution, resources, processes and scheduling. DYNA 2017, 92, 637–642. [Google Scholar]
- Burleigh, D.; Vavilov, V.P.; Pawar, S.S. The influence of optical properties of paints and coatings on the efficiency of infrared nondestructive testing applied to aluminum aircraft structures. Infrared Phys. Technol. 2016, 77, 230–238. [Google Scholar] [CrossRef]
- Kim, D.; Udpa, L.; Udpa, S. Remote field eddy current testing for detection of stress corrosion cracks in gas transmission pipelines. Mater. Lett. 2004, 58, 2102–2104. [Google Scholar] [CrossRef]
- Teitsma, A.; Takach, S.; Maupin, J.; Fox, J.; Shuttleworth, P.; Seger, P. Small diameter remote field eddy current inspection for unpiggable pipelines. J. Press. Vessel Technol. 2005, 127, 269–273. [Google Scholar] [CrossRef]
- Krenkel, W.; Heidenreich, B.; Renz, R. C/C-SiC composites for advanced friction systems. Adv. Eng. Mater. 2002, 4, 427–436. [Google Scholar] [CrossRef]
- Zhang, Y.; Li, D.; Zhou, Z. Time reversal method for guided waves with multimode and multipath on corrosion defect detection in wire. Appl. Sci. 2017, 7, 424. [Google Scholar] [CrossRef]
- Worden, K.; Farrar, C.R.; Haywood, J.; Todd, M. A review of nonlinear dynamics applications to structural health monitoring. Struct. Control Health Monit. 2008, 15, 540–567. [Google Scholar] [CrossRef]
- Jiao, J.P.; Zheng, L.; Song, G.R.; He, C.; Wu, B. Vibro-acoustic modulation technique for micro-crack detection in pipeline. In Proceedings of the 7th International Symposium on Precision Engineering Measurements and Instrumentation, Lijiang, China, 7–11 August 2011. [Google Scholar]
- Duffour, P.; Morbidini, M.; Cawley, P. Comparison between a type of vibro-acoustic modulation and damping measurement as NDT techniques. NDT & E Int. 2006, 39, 123–131. [Google Scholar]
- Liu, P.; Sohn, H.; Jeon, I. Nonlinear spectral correlation for fatigue crack detection under noisy environments. J. Sound Vib. 2017, 400, 305–316. [Google Scholar] [CrossRef]
- Hess, P.; Lomonosov, A.M.; Mayer, A.P. Laser-based linear and nonlinear guided elastic waves at surfaces (2D) and wedges (1D). Ultrasonics 2014, 54, 39–55. [Google Scholar] [CrossRef] [PubMed]
- Gusev, V.; Chigarev, N. Nonlinear frequency-mixing photoacoustic imaging of a crack: Theory. J. Appl. Phys. 2010, 107, 124905. [Google Scholar] [CrossRef]
- Chigarev, N.; Zakrzewski, J.; Tournat, V. Nonlinear frequency-mixing photoacoustic imaging of a crack. J. Appl. Phys. 2009, 106, 036101. [Google Scholar] [CrossRef]
- Liu, P.; Sohn, H. Damage detection using sideband peak count in spectral correlation domain. J. Sound Vib. 2017, 411, 20–33. [Google Scholar] [CrossRef]
- Yoder, N.C.; Adams, D.E. Vibro-acoustic modulation utilizing a swept probing signal for robust crack detection. Struct. Health Monit. Int. J. 2010, 9, 257–267. [Google Scholar] [CrossRef]
- White, R.M. Generation of elastic waves by transient surface heating. J. Appl. Phys. 1963, 34, 3559–3569. [Google Scholar] [CrossRef]
- Nichols, J.M. Structural health monitoring of offshore structures using ambient excitation. Appl. Ocean Res. 2003, 25, 101–114. [Google Scholar] [CrossRef]
- Martínez, S.; Lamikiz, A.; Ukar, E.; Calleja, A.; Arrizubieta, J.A.; López De Lacalle, L.N. Analysis of the regimes in the scanner-based laser hardening process. Opt. Lasers Eng. 2017, 90, 72–80. [Google Scholar] [CrossRef]
- Overbey, L.A.; Olson, C.C.; Todd, M.D. A parametric investigation of state-space-based prediction error methods with stochastic excitation for structural health monitoring. Smart Mater. Struct. 2007, 16, 1621–1638. [Google Scholar] [CrossRef]
- Liu, G.; Mao, Z.; Todd, M.; Huang, Z. Localization of nonlinear damage using state-space-based predictions under stochastic excitation. Smart Mater. Struct. 2014, 23, 025036. [Google Scholar] [CrossRef]
- Liu, G.; Mao, Z.; Todd, M. Damage detection using transient trajectories in phase-space with extended random decrement technique under non-stationary excitations. Smart Mater. Struct. 2016, 25, 115014. [Google Scholar] [CrossRef]
- Takens, F. Detecting Strange Attractors in Turbulence, in Dynamical Systems and Turbulence; Springer: Berlin/Heidelberg, Germany, 1981; pp. 366–381. [Google Scholar]
- Fraser, A.M.; Swinney, H.L. Independent coordinates for strange attractors from mutual information. Phys. Rev. A 1986, 33, 1134–1140. [Google Scholar] [CrossRef]
- Cao, L.Y. Practical method for determining the minimum embedding dimension of a scalar time series. Phys. D Nonlinear Phenom. 1997, 110, 43–50. [Google Scholar] [CrossRef]
- Pecora, L.M.; Carroll, T.L. Discontinuous and non-differentiable functions and dimension increase induced by filtering chaotic data. Chaos 1996, 6, 432–439. [Google Scholar] [CrossRef] [PubMed]
- Overbey, L.A.; Todd, M.D. Damage Assessment using generalized state-space correlation features. Struct. Health Monit. Int. J. 2008, 7, 347–363. [Google Scholar] [CrossRef]
- Nichols, J.M.; Todd, M.D.; Wait, J.R. Using state space predictive modeling with chaotic interrogation in detecting joint preload loss in a frame structure experiment. Smart Mater. Struct. 2003, 12, 580–601. [Google Scholar] [CrossRef]
- Lei, Y.G.; He, Z.J.; Zi, Y.Y.; Chen, X. New clustering algorithm-based fault diagnosis using compensation distance evaluation technique. Mech. Syst. Signal Process. 2008, 22, 419–435. [Google Scholar] [CrossRef]
- Aindow, A.; Dewhurst, R.J.; Hutchins, D.A.; Palmer, S.B. Characteristics of a laser-generated acoustic source in metals. In Proceedings of the European Conference on Optical Systems and Application, Utrecht, The Netherlands, 23–25 September 1980; Volume 236, pp. 478–485. [Google Scholar]

















© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, Y.; Yang, S.; Liu, X. Detection and Quantification of Damage in Metallic Structures by Laser-Generated Ultrasonics. Appl. Sci. 2018, 8, 824. https://doi.org/10.3390/app8050824
Liu Y, Yang S, Liu X. Detection and Quantification of Damage in Metallic Structures by Laser-Generated Ultrasonics. Applied Sciences. 2018; 8(5):824. https://doi.org/10.3390/app8050824
Chicago/Turabian StyleLiu, Yongqiang, Shixi Yang, and Xuekun Liu. 2018. "Detection and Quantification of Damage in Metallic Structures by Laser-Generated Ultrasonics" Applied Sciences 8, no. 5: 824. https://doi.org/10.3390/app8050824
APA StyleLiu, Y., Yang, S., & Liu, X. (2018). Detection and Quantification of Damage in Metallic Structures by Laser-Generated Ultrasonics. Applied Sciences, 8(5), 824. https://doi.org/10.3390/app8050824