1. Introduction
Liver diseases are among the most life-threatening diseases worldwide. Among the different kinds of liver lesions, liver cancer has a high incidence rate and high mortality rate in the countries of East Asia, Southeast Asia, sub-Saharan Africa, and Melanesia [
1]. Liver abscess is less common than liver cancer. However, if it is not detected in time and treated in the proper manner, it may cause many serious infectious complications, even death. Liver biopsy is often used to evaluate liver diseases. It permits doctors to examine a liver and provides helpful information to make high-accuracy predictions. Along with those undeniable benefits, it may cause pain, infection or other injuries that hinder later treatments.
To reduce the unnecessary number of biopsy cases, other noninvasive methods for diagnosis have been applied widely, especially imaging techniques such as ultrasound (US) (e.g., see [
2,
3,
4,
5,
6,
7,
8,
9]), computed tomography (CT) (e.g., see [
4,
10,
11,
12,
13,
14,
15]) or magnetic resonance imaging (MRI) (e.g., see [
2,
3,
12,
16]). Among those methods, ultrasound imaging, with unique advances advantages such as no radiation, low cost, easy operation, and noninvasiveness, is widely used to visualize the liver for clinical diagnoses. Therefore, it could provide visual information for doctors to identify the state of disease. Nevertheless, the diagnoses are significantly affected by the quality of ultrasound images as well as the doctors’ knowledge and experience. For inexperienced clinicians, it may be not easy to distinguish between liver cancers and liver abscess.
To overcome the obstacles mentioned above, it would be helpful to develop a computer-aided diagnosis (CAD) system (e.g., see [
15,
17,
18]). By using image processing and machine learning techniques, a well-built system could help clinicians effectively and objectively distinguish liver diseases. Multiple scientists have studied the classification of liver diseases based on ultrasound images. For example, Nicholas et al. first exploited textural features to discriminate between liver and spleen of normal humans [
19]. Richard and Keen utilized Laws’ five-by-five feature mask and then applied a probabilistic relaxation algorithm to the segmentation [
20]. Many textural features were used by Pavlopoulos et al. for quantitative characterization of ultrasonic images [
21]. Bleck et al. used the random field model to distinguish the four states of the liver [
22]. The models proposed by Kadah et al. and Gebbinck et al. combined neural networks and discriminant analysis to separate the different liver disease [
23,
24]. Pavlopoulos et al. improved their model by using fuzzy neural networks to process the features [
25]. Horng et al. evaluated the efficiency of the textural spectrum, the fractal dimension, the textural feature coding method, and the gray-level co-occurrence matrix in distinguishing cirrhosis, normal samples, and hepatitis [
26]. Yang et al. developed an algorithm for classifying cirrhotic and noncirrhotic liver with the spleen-referenced approach [
27].
As mentioned above, analyzing and classifying images presenting organ lesions to differentiate benign and malignant lesions is a goal shared by many researchers. There are still few clinically relevant studies on ultrasound imaging to explore the CAD-based differential diagnosis of hepatocellular carcinoma and liver abscess, even though many studies have analyzed the characteristics of hepatocellular carcinoma (HCC) (e.g., see [
28,
29]) or liver abscess (e.g., see [
30,
31]). Recently, many methods have been proposed to extract the features from ultrasound images. For instance, first- and second-order statistics have been used (e.g., see [
32]). Other approaches based on wavelet transform (e.g., see [
33]), Gabor filter (e.g., see [
34]), monogenic decomposition (e.g., see [
35]), or fractal analysis (e.g., see [
36]) were also proposed.
A CAD system to distinguish between liver cancer and liver abscess has not been discussed. The main objective of this paper is to develop a reliable CAD system to distinguish between hepatocellular carcinoma (HCC), i.e., the most common type of primary liver malignancy and a leading cause of death in people with cirrhosis worldwide, and liver abscess based on the support vector machine (SVM) method [
37,
38,
39,
40,
41] and ultrasound images of textural features. To date, there is no algorithm that is best in machine learning. A good classifier depends on the data. Some algorithms work with certain data or applications better than others. The major advantage of SVM is the need for fewer parameters to make it operational with high accuracy rates, and various features can be extracted. However, the textural feature applied the most is the gray-level co-occurrence matrix (GLCM) (e.g., see [
42,
43,
44,
45,
46]). GLCM feature extraction, proposed by Haralick [
42] in 1973 to analyze an image as a texture, belongs to the second-order statistics. GLCM means a tabulation of the frequencies or how often a combination of pixel brightness values in an image occurs. In this paper, the other method we used to analyze the ROIs is the gray-level run-length matrix (GLRLM) (e.g., see [
47,
48,
49,
50,
51]). It was first proposed by Galloway in 1975 with five features [
47]. GLRLM is a matrix including the texture features that can be extracted for texture analysis. In 1990, Chu et al. [
48] suggested two new features to extract gray-level information in the matrix before Dasarathy and Holder [
49] offered another four features following the idea of a joint statistical measure of gray level and run length. Tang [
50] provided a good summary of some features achieved by the GLRLM. In this paper, we compared the results from the popular features of the GLCM and the gray-level run-length matrix (GLRLM).
In this paper, three feature selection models—(i) sequential forward selection (SFS) [
52,
53], (ii) sequential backward selection (SBS) [
53,
54], and (iii) F-score [
55]—are adopted to distinguish the two liver diseases. Marill and Green introduced a feature selection technique using the divergence distance as the criterion function and the SBS method as the search algorithm [
52,
53]. Whitney discussed its ‘bottom-up’ counterpart, known as SFS [
53,
54]. In this research, a large number of features are included, comprising 96 features from each sample. If all of them are used to train a classifier, it not only takes too much time but also cannot easily achieve high accuracy. To reduce the processing time and improve the accuracy, it is necessary to search for the important features from the feature set. Then, the crucial features of the samples are used to train and test by SVM. We took several steps to achieve this goal. First, in the ultrasound images, the liver lesions are marked by experienced physicians and the regions of interest (ROIs) are circled inside a red boundary, as illustrated in
Figure 1, meaning that part of the liver lesion is located inside the red boundary of the whole-liver image. Second, all features are extracted from the collected ROIs. Third, several feature selection processes are carried out to optimize the feature set. Finally, the optimal feature sets are used to train and test by SVM.
3. Feature Selection
Feature selection has been an interesting research field in machine learning, pattern recognition, data mining, and statistics. The main idea of feature selection is to eliminate redundant features that contain little or no predictive information while keeping the useful ones. To find optimal features for classification, researchers have proposed several methods to analyze the feature set. In fact, the effectiveness of features on classification is highly problem-dependent. Extracted features could perform very well for one problem but may give poor performance for others. Hence, we must pick proper features for the given problem at hand. Ultimately, from various feature extraction methods, we need to find a set of features that is optimal for the problem. In this research, we use sequential forward selection (SFS) [
52,
53], sequential backward selection (SBS) [
53,
54], and F-score [
55] to find the optimal feature subset.
3.1. Sequential Forward Selection (SFS)
SFS [
52,
53] begins by evaluating all samples of a dataset that consist of only one input attribute. In other words, we start from the empty set and sequentially add feature
, which results in the highest-valued objective function
. Its algorithm can be broken down into the following steps:
Step 1: Start with empty set .
Step 2: Select the next best feature with . In our case, the objective function is based on the classification rate from a cross-validation test. The mean value of a 10-fold cross-validation test is used to evaluate the feature subset.
Step 3: Update = and set .
Step 4: Go to Step 2.
This procedure continues until a predefined number of features are selected. According to the above process, we see that the search space is drawn such as an ellipse to emphasize the fact that there are fewer states towards the full or empty sets. To find the optimum input feature set overall, the easiest means is an exhaustive search. However, this is very expensive. Compared with an exhaustive search, forward selection is much cheaper. SFS works best when the optimal subset has a small number of features, and the main disadvantage of SFS is that it is unable to remove features that become obsolete after the addition of other features.
3.2. Sequential Backward Selection (SBS)
Contrary to SFS, SBS [
53,
54] works in the opposite way. SBS starts from a full set of features and sequentially eliminates the worst feature
to result in the highest-valued objective function
. Its algorithm can be broken down into the following steps:
Step 1: Start with full set
Step 2: Eliminate the worst feature with . The objective function is based on the classification rate from a cross-validation test. The mean value of the 10-fold cross-validation test is used to evaluate the feature subset.
Step 3: Update = and set .
Step 4: Go to Step 2.
This procedure continues until a predefined number of features are left. SBS usually works best when the optimal feature subset has a large number of features since SBS spends most of its time visiting large subsets.
3.3. F-Score
F-score [
55] is a technique that measures discrimination. Given training vectors
,
, if the number of positive and negative instances are
and
, respectively, then the F-score of the
ith feature is calculated as in Equation (41)
where
are the averages of the
ith features of the whole, positive, and negative data, respectively, and
are the
ith features of the
kth positive and negative sample, respectively. F-score indicates the discrimination between the positive and negative sets; therefore, the larger the F-score, the more likely this feature is to be more discriminative. Thus, we could consider this score as a criterion for feature selection. A disadvantage of this method is that it cannot reveal shared information between features [
55]. In the example, both features have low values of F-score; however, the set of them classifies the two groups precisely.
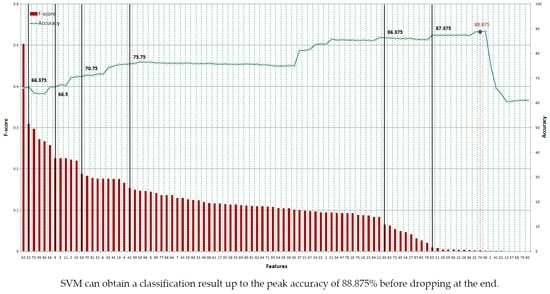
In spite of this drawback, F-score is simple and generally quite effective. We order all features based on F-score and then use a classifier to train/test the set that includes the feature with the highest F-score. Then, we add the second highest F-score feature to the feature set before training and testing all of the dataset again. The procedure is repeated until all features are added to the feature set.
5. Performance Evaluation
To reduce the variability of the prediction performance, a cross-validation test is usually used to evaluate the performance of the proposed system. It is one of the most popular methods to evaluate a model’s prediction performance. If a model was trained and tested on the same data, it would easily lead to an overoptimistic result. Therefore, the better approach, the holdout method, is to split the training data into disjoint subsets.
As it is a single train-and-test method, the error rate we got resulted from an ‘unfortunate’ split. Moreover, in some cases of a lack of samples, we cannot afford the luxury of setting. The drawbacks of the holdout can be overcome with a family of resampling methods, called cross-validation. Two well-known kinds of cross-validation are leave-one-out cross-validation (LOOCV) and k-fold cross-validation.
In
k-fold cross-validation, the total samples are randomly partitioned into
k groups, which have the same size. Of the
k groups, one group is for testing the model, while the remaining (
k − 1) groups are used as training data. This process is repeated
k times (the folds) until all groups are tested. Then, the results from the
k experiments can be averaged to produce a single estimation. Thus, the true accuracy is estimated as the average accuracy rate
The advantage of this method is that all samples are used for both training and validation, and each observation is used for validation only one time. Although 10-fold and 5-fold cross-validation are commonly used, in general k is an unfixed parameter.
Leave-one-out cross-validation could be considered a degenerate case of k-fold cross-validation where k is the total number of samples. Consequently, for a data set with N samples, LOOCV performs N experiments. In each experiment, only one sample is used for testing, while N-1 samples left are for the training process.
In this research, we use 10-fold cross-validation for performance evaluation. The classification results in four kinds of value: true positive (TP), true negative (TN), false positive (FP), and false negative (FN) (shown in
Table 3).
Where ‘true’ and ‘false’ are intended for result correction, while ‘positive’ or ‘negative’ signifies the tumor is either HCC or liver abscess. Based on the information, we calculate the accuracy factors as in Equation (43), which describes the performance of classifiers