1. Introduction
Nowadays, great concerns about energy crisis and environment problems are encouraging more efficient energy management and consumption. Residential and commercial buildings consume about 32% of the global energy use, in which usually there are multi-energy demands, such as electricity and heat [
1]. It is particularly important to change the existing energy systems which are individually designed to operate separately, and to build various energy systems as an integrated whole in order to improve the overall energy utilization efficiency and lower environmental pollution. Therefore, some coupled energy systems, such as the multiple-energy carriers system (MCES) [
2] and the multi-energy system (MES) [
3], have been investigated in recent years. The essential characteristics of these systems is the interaction of diverse forms of energy, such as heat power, electrical power, nature gas, renewable energies and so on. However, the uncertainty and randomness of the MES considering electric vehicles (EVs) and renewable energy are still a challenge for scheduling optimization in MES.
The integration of EVs and combined heat and power (CHP) units have an increasing impact on the distribution grid and will change the buildings’ electricity consumption and supply. In general, EVs are parked for more than 90% of the time and EVs charging/discharging flexibility can be utilized fully, although the charging/discharging is limited by battery limitations, the mobility objectives, the available power ratings and battery state of charge (SOC). Consequently, as one of the most important components in energy systems due to their advantages of flexible charging/discharging and zero emission, EVs can connect to the MES in the form of Grid-to-Vehicle (G2V) or Vehicle-to-Grid (V2G) [
4]. However, on one hand, the electricity consumption of EVs in G2V mode may lead to peak loads, higher resistive losses, voltage deviations, and phase unbalance in the grid [
5]; on the other hand, in contrast to other electrical equipment, the integration of EVs simultaneously connected in parking stations could be considered as a potential source for the demand respond in the MES. However, the uncertain arrival/departure time induced stochastic availability of aggregated EVs should be considered carefully. As a significant means to improve energy efficiency, CHP units have received increasing attention owing to their ability in providing electrical and thermal power simultaneously, but they have to remain on certain constrained electric power output to meet the heat loads’ demand. Therefore, the scheduling coordination between the aggregated EVs and CHP units in MES is crucial to improve the system operational flexibility and enhance energy efficiency.
Extensive research has been conducted on the optimal operation of MES, which is modeled based on the integration of EVs, CHPs, or other renewable energies. Ref. [
6] presented an approach to solve the CHP unit commitment problem in the presence of plug-in EVs as small portable generation units in addition to typical generation constraints. In Ref. [
7], a multi-objective optimization algorithm was proposed for minimization of energy cost and emissions for residential microgrids considering combined cooling heating and power (CCHPs), electric and thermal energy storage and EVs. A two-stage stochastic programing was used to minimize the operational cost of a microgrid by using scenario generation and a reduction technique [
8]. Ref. [
9] investigated the optimization and energy management in smart homes considering photovoltaic, wind, and battery storage systems with integration of EVs through a heuristic technique. Ref. [
10] provided a number of stochastic programming models for optimal decision-making under uncertainty in electricity markets and electric energy systems with a large integration of non-dispatchable sources. A closed-loop V2G control to achieve both the frequency regulation and the EV charging demands was studied by a hierarchical control structure considering the uncertain dispatch in Ref. [
11]. In Ref. [
12], an optimal energy management scheme to charge or discharge EVs efficiently was developed by considering vehicle-to-building (V2B), renewable energy source (RES) and energy storage system (ESS) considering driver behavior. A robust stochastic shortest path model to stochastically match the EV charging load with the wind supply was studied in Ref. [
13]. Ref. [
14] developed a multi-objective model for Multi-Energy Complementary System (MECS) operation considering different operation constraint conditions under three objective functions. Ref. [
15] analyzed the unbalance of plug-in EVs home charging in distribution network by stochastic load model. In Ref. [
16], an Eco-town based MES in UK was simulated to research the optimal size and operation strategy of mixed technologies such as fuel cell, CHP, gas boiler and PV to meet the electrical and thermal loads. Ref. [
17] developed a method for scheduling EVs charging based on probabilistic models. The authors in [
18] studied a stochastic model of the home energy management (HEM) considering the uncertainties of EVs availability and small-scale renewable energy generation, as well as the customers’ satisfaction by developing a response fatigue measure. Ref. [
19] proposed leveraging day-ahead power market and time-of-use electricity, and use stochastic programming to address the uncertainties in EV charging demand.
In the above literature on integrated electricity and the heat system, the operational optimization modelling of electricity and heat energy as a whole, considering various CHP units with complementary properties, is limited. It is well known that, in MES, the electricity demand is independent from heat demand; on the contrary, the electricity generation is coupled with heat production due to the constraints on operational characteristics of CHP units, which makes the coordinated optimization intractable under the constraints of multi-energy supply/demand balance. Consequently, how to coordinately schedule the multi-energy generation in MES with various CHPs, i.e., the fixed or variable heat-to-electricity ratio, is imperative. Moreover, on the uncertainties of EVs included in MES, some work used the deterministic modeling to formulate the scheduling of MES, without further discussing the stochastic model of EV availability and driving pattern [
7,
9,
11]; in other work, although the stochastics were considered, the coordination between electricity and thermal multi-energy was involved simply. As for the costs of EVs’ batteries degradation, little research included it in the coupled scheduling optimization of multi-energy, which is important for realizing the high efficiency operation control for CHP units with the unmatched heating and electric power demands [
12,
13,
14,
15,
16,
17,
18,
19].
As the driver information and the stochastic model of EVs availability are not easily exploited by classical control strategies, model predictive control (MPC) appears to be suitable for this purpose. Recently, MPC has drawn the attention of the power system community and consequently the research to show the advantages of applying MPC to dynamic economic dispatch with the uncertainties considered have been implemented. Initially, the EVs and CHP power coordination is made for the MES in order to create a power balance between power generation and demand. Then, this method optimizes a control sequence over a receding horizon to predict the future system behavior [
20]. MPC is based on iterative, finite-horizon optimization of the controlled model. In MPC, at each time step, the solution to the optimal control problem is solved over a certain pre-defined horizon using the current state of the system as the initial state. The optimization calculates a control sequence for the whole horizon such that the selected objectives are minimized, but only the control action for the next time step is implemented in the system [
21]. In Ref. [
20], the authors develop an approach for driver-aware vehicle control based on stochastic model predictive control with learning (SMPCL) combining the learning of a Markov chain that represents the driver behavior and a scenario-based approach for stochastic optimization. Ref. [
22] presented an integrated model predictive control (IMPC) method that combined power management and adaptive velocity control during vehicle-following scenarios in reality, in order to synergistically examine driving safety and fuel economy during vehicle following scenarios of plug-in hybrid electric vehicles (PHEVs).
In this paper, an MPC method based coordinated scheduling optimization for MES is proposed, in which the stochastic nature of EV availability respectively in office or residential sites is investigated considering people’s driving patterns, and, moreover, the coordination of two kinds of complementary CHPs is achieved in satisfying the electricity and thermal demands. The main contribution of this paper can be summarized into the following aspects: (1) The uncertain EVs available charging/discharging electricity energy, respectively, in offices and residential buildings is described considering peoples’ daily driving pattern, and represented by a number of scenarios generated by scenario generation and reduction techniques; (2) A stochastic MPC approach based electricity-heat coupled MES coordinated scheduling is developed, aiming to achieve the most economic operation in terms of operational costs and EV batteries’ degradation costs, while considering operational constraints of various CHPs with complementary properties, which is formulated by a mixed-integer linear programming (MILP) problem and solved by the mature software Cplex. (3) For office or residential buildings, the working modes of EVs are analyzed and discussed; moreover, the energy generation efficiencies of two kinds of CHPs with fixed and variable heat-to-electricity ratio are analyzed.
The rest of this paper is organized as follows: in
Section 2, MES structures are introduced, including the system architecture and the components of EVs and CHPs.
Section 3 illustrates the stochastic MPC approach for optimal scheduling coordination of MES, including the model and the solving procedure. In
Section 4, the simulation results and discussions are described, and two cases are studied to demonstrate the proposed approach. Finally, the paper is concluded in
Section 5.
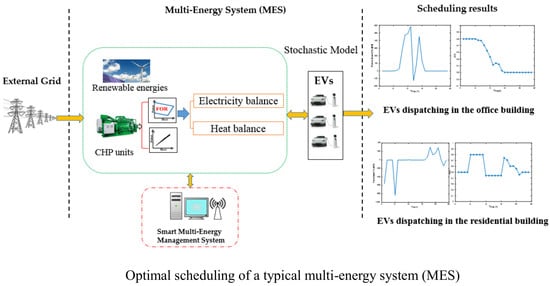
2. Multi-Energy System Structure
MES includes electrical loads, thermal loads, controllable EVs, CHPs, energy storage devices, distributed renewable energy, and the associated electricity, heating and information transmission networks. A typical MES structure is shown in
Figure 1. The MES can operate in islanded mode or grid-connected mode by connecting with the external main grid.
The increasing inclusion of plug-in EV has the potential of not only bringing benefits by reducing the on-peak demand, but also improving the economic efficiency. Consequently, in the MES, the scheduling of aggregated EVs is being promoted by persuading the EV owners to participate in the scheduling program. On one hand, the aggregated EVs can be considered as a battery energy storage device in MES when an electricity power imbalance arises or when the buying electricity price from main grid is relatively higher; on the other hand, the aggregated EVs can be regarded as a bulk electricity demand to be charged when the electricity price is cheaper or the load is lower. Consequently, the coordination between EVs and other energy generators in MES has been receiving increasing attention from the researchers. However, there exists an intractable challenge, i.e., the flexibility of available EV charging or discharging electric power and capacity is uncertain and depends on the peoples’ daily commuting behaviors, for example when to arrive in the office and when to go home.
As an important energy coupling component, CHP units can supply both electrical and thermal power and can impose significant impacts on the operation of MES. The gas turbine CHP consists mainly of an air compressor, a gas combustion chamber, a turbine, a control system and related auxiliary equipment. The CHP units are classified as backpressure and extraction-condensing units. As shown in
Figure 2, the produced thermal power of the back-pressure units depends linearly on the output of the electricity power, thus leading to a limited operation flexibility. For the extraction-condensing units, the operation region in
Figure 3 is described as an irregular quadrilateral [
23]. Obviously, the feasible operation region (FOR) of the extraction-condensing units is much bigger than that of the backpressure units [
24]. The effective coordination between these two types of complementary CHPs makes it possible to simultaneously satisfy electricity and heat demands. In addition, electric heater and heat storage are also installed in MES, in order to offer more flexibility.
The electricity utility company makes a direction guide for charging time of EVs owners by setting peak and valley electricity price for 24 h in a day. The price of natural gas is usually fixed during the period of a day.
3. Stochastic MPC Approach for Coordinated Scheduling Optimization of MES
The studied MES operates in main grid connected mode. In the MES, two types of CHPs with complementary properties are considered, and the EVs are aggregated to be controlled as an electricity load or an electricity supplier. The electricity demands in the MES are satisfied by the main grid, CHPs and EVs; and the thermal demands are provided by two kinds of CHP units. The objective of coordinated scheduling optimization is to achieve the most economic operation while satisfying electricity and thermal power supply/demand balance, the operational constraints of CHP units and EVs.
The stochastic MPC based scheduling optimization of MES, considering the coordination of electricity and heat supplies, is formulated into an MILP problem. The optimization process is composed of two steps. In the first step, the stochastic model of EVs availability is established by using scenario generation and reduction; and, in the second step, the MILP problem is solved, in which minimizing the operation cost is considered as the objective, while considering the supply and demand balance of electricity and heat power and other operational constraints. The schematic overview of the stochastic MPC approach for MES coordinated scheduling optimization is depicted in
Figure 4.
3.1. Modelling of Electric Vehicles’ Stochastic Availability
It is assumed that the EV owners immediately connect their EVs to the charging/discharging station in the office or residential building in the morning when they arrive at work and in the evening when they arrive home. In office buildings or residential communities, EV characteristics, in terms of available charging/discharging energy, are quite unique and distinctive, closely depending on peoples’ commuting behaviors. In addition, it is worthwhile to note that the availability of EV charging/discharging is quite uncertain, considering the stochastic individual arrival and departure time.
According to the study which uses driving pattern data of a large number of customers from the National Household Travel Survey (NHTS) [
25], the probability distribution of arrival time to the office or home and departure time from the office or home is developed. The arrival/departure time can be represented by a normal distribution and its probability density function (PDF) is described as
where
is the probability of arrival/departure time, and
and
are its mean value and standard deviation, respectively.
Take the office arrival time as an example to illustrate this. It is assumed that, in the researched office building, the number of EVs participating in scheduling management is
NEV. For all the EVs, their arrival times are uncertain variables. Usually, sampling is implemented to generate representative samples, aimed to reflect the distribution of each random variable. For an EV
i, the uncertainty of its office arrival time is represented by
NS scenarios generated by a Latin Hypercube Sampling (LHS) method considering PDF described in Equation (1) [
26]. It is assumed that the arrival events of EVs are independent from each other, i.e., the random variable
for EV
i is independent from
. In order to minimize the undesired correlations between the generated samples of different random variables, a permutation method is needed. Cholesky decomposition is a good permutation method, which is helpful for reducing the correlation among the samples of different random variables and can also further improve the performance of LHS. Then,
NS scenarios of
NEV random variables
are derived. For scenario
s , the available state
of EV
j at time
t is defined as
. The available EV number
at time
t can be calculated by
.
NS scenarios of random vector can be generated using the aforementioned procedure. However, it is time consuming to solve the stochastic scheduling optimization using NS scenarios. The very large set of scenarios has to be approximated by a small number of scenarios using a scenario reduction technique. Here, the backward method is subsequently applied to make the reduced set of scenarios be as close as possible to the original stochastic process.
The probability of each scenario in
NS scenarios is
, and
. The scenarios set is
. The set
S and
DS represents all scenarios before and after reduction, respectively. Calculating all the distances of a couple of scenarios
. For the scenario
k, the nearest one is
r, and calculates the minimum distance of (
k,
r) scenario couples,
. After that,
should be characterized by
, and find the nearest scenario
d,
. Then, the extra scenarios are removed by repeating the above steps, and
DS is the reduced scenarios set with
DNS scenarios [
27].
Step (1) In the first calculation, the
DS set is initially empty, the following equation to determine the distance of all couples of scenarios should be applied:
Step (2) For each scenario
k, find the minimum distance between scenario
r and
k by the following equation:
Step (3) The distance of probability distribution
and
should be characterized by Equations (4) and (5), respectively, and find the nearest scenario
d:
Step (4) New scenarios set are generated by the following:
Step (5) Return to Step (2) and repeat; then, the reduced scenario set will be obtained.
The flowchart of a scenario reduction method is shown in
Figure 5. The distance of probability distribution is used to be the standard for scenario reduction. The suitable scenario number is determined by balancing the computational burden and scheduling optimization accuracy. The reduced scenarios of available EV number are denoted by
[
27,
28].
3.2. Modelling of Combined Heat and Power Units
The first type of CHP uses a gas turbine or internal combustion reciprocating engine with a fixed heat-electricity ratio, which can be modeled as
where the parameters
and
are considered constant,
and
are the generated heat and electricity power, and
is the power of the consumed natural gas.
The generated electricity power is constrained by
The second type of CHP unit uses extraction steam turbines that can be operated within a wide range of heat-to-electricity ratio. In Equations (10)–(12), the feasible operation region of the CHP is described by a polygon via four lines as shown in
Figure 3, where the lines with the slope
and
(
), respectively, define the lower and the upper limits of electric power output with respect to any level of heat power output [
28,
29,
30]. For the electricity power generation
and the by-product heat power generation
, the power of the consumed natural gas by CHP unit is computed in Equation (12):
The natural gas consumption (m3) by the two CHP units is described as
where
(kWh/m3) is the lower heating value of natural gas.
3.3. Model of MPC Based Optimal Scheduling
MPC strategies are quite appealing for energy scheduling of MES, since they allow for the implementation of control actions that anticipate future events such as variations of EVs availability, heat demand and electricity demand. The MPC rolling optimization method usually involves three time sequences: scheduling time sequence, predicting time sequence and controlling time sequence, which is based on iterative, finite-horizon optimization of the controlled model. The rolling optimization method guarantees the optimization of real-time control action by sampling and calculating online [
20].
Two 0–1 binary variables
and
and two continuous variables
(
) and
(
) are introduced for describing the SOC and charging/discharging power of the aggregated EVs’ batteries. The charging/discharging power and SOC of EVs are modelled as follows:
is
i-step-ahead dispatched discharging (
> 0)/charging (
< 0) power of the aggregated EVs.
is
i-step-ahead dispatched state of charge of aggregated EVs,
is the maximum charging/discharging power of a EV,
is the capacity of a EV battery in kWh, and
and
are charging and discharging efficiency of EV.
The
SOC is limited by its upper and lower boundaries
Operational cost can be employed as one of the main objective functions in MES scheduling. The purpose of MES scheduling optimization is to determine the amount of energy generated by the controlled units in the presence of uncontrolled units in a way that the operational cost is minimized while complying with the various operational constraints [
30,
31]. The optimization objective is to minimize the expected value of the total operating cost during the predictive horizon:
where
denotes the length of prediction horizon,
is the index of time step in the prediction horizon with
= 0 being the current time,
is
-step-ahead scheduled electricity power exchange between the MES and the external grid,
is the
-step-ahead predictive price of exchanged electricity,
is the cost of natural gas,
is the
-step-ahead scheduled value of natural gas consumption,
is the initial investment cost of the available EVs in scenario
s,
is the EVs’ batteries life loss proportion of total investment cost, and
is the probability of scenario
s after scenarios reduction.
The service life of EVs’ batteries usually degrades when subjected to repeated charge/discharge cycles. Usually, the battery manufacturers report the relationship between capacity degradation and the number charge/discharge cycle with the fixed operating strategy employed, i.e., the charge/discharge is complete or half cycle. When EVs’ batteries are scheduled in practical application, the real charging/discharging process is complicated, representing local cycle, non-complete or complete charging, and so on. Consequently, when considering the degradation cost of EVs’ batteries in the optimization objective, the batteries’ life loss cost, approximated in the last item on the right side of Equation (20), is included. Usually for an EV’s battery, the total cumulative charging/discharging Ah throughput during the whole life cycle can be obtained by manufacturers, denoted by
. The actual cumulative Ah throughput in a certain period of time is employed to measure the life loss cost of batteries, and then it can be expressed as [
32,
33,
34,
35,
36,
37]
The initial investment cost
can be defined as
In addition to the operation constraints of CHP units and EVs represented in Equations (7)–(19), the supply and demand balance of electricity and thermal energy are considered as follows:
(1) Electricity power supply and demand balance
The electricity supply and demand balance should be imposed, which is described as follows:
where
and
are
i-step-ahead scheduled values of CHP electricity power generation, and
is the electricity demand.
Power exchange between the MES and the external main grid is constrained by
where
is the maximum power purchasing from external grid.
(2) Thermal power supply and demand balance
Practically, it is not necessary that the thermal supply is absolutely balanced by its demand; on the contrary, maintaining the thermal supply and demand balance within an accepted range is desirable. Consequently, the thermal supply and demand balance should follow the following constraints:
where
and
are the lower and upper allowed fluctuation coefficients.
3.4. Solving Procedure of MPC Based Optimal Scheduling
In the proposed MPC method, the solution to the optimal control problem of MES is solved over a certain pre-defined horizon using the current state of the system as the initial state at each time step. The optimization calculates a control sequence for the whole horizon such that the selected objectives are minimized, but only the control action for the next time step is implemented; the horizon is shifted forward and the process is then repeated at the next time step [
21]. A finite-horizon optimal control problem is solved repeatedly, the procedure of which is illustrated by
Figure 6. In this simulation, the prediction horizon of MPC is chosen as
. Firstly, the MPC controller will calculate the scheduling results over four time periods at the current time constant. Then, a four-dimensional optimal controller can be obtained; however, only the first component of this solution will be actually executed at this time instant. Finally, the optimization horizon will move one step forward, and the optimization will be repeated on the next interval of four time periods with the updated initial values.
The procedure of applying the proposed stochastic MPC algorithm in the operation optimization of MES is illustrated as follows:
- Step (1)
When t = 0, obtain the reduced scenarios of available EV number at each hour by LHS and scenario reduction techniques, and initialize the parameters.
- Step (2)
Solve the stochastic MPC optimization model over the following prediction time horizon T, i.e., the objective (20) and the constraints Equations (7)–(19) and Equations (21)–(25), with respect to time t via Cplex.
- Step (3)
The prediction time horizon is shifted forward (i.e., the time instant moves to t = t + 1) and implement the first control action, i.e., the scheduled results of , and the expected value of the aggregated EVs power on the system.
- Step (4)
Update the initial parameters, return to Step (2) and repeat.
In the proposed approach, the short-term-ahead scheduling of MES is formulated as an MPC problem. During the considered prediction horizon, the optimization objective is to minimize the total operational cost, the constraints for the power supply/demand balance are applied, and the bounds for charging/discharging power of EVs are imposed for a total number of scenarios of uncertain EVs’ model. With the MPC approach considering the scenario optimization, the operational cost can be minimized while the supply and demand balance of electricity and heat is achieved by coordinating the supply of CHPs and uncertain available EVs properly.