Effects of Configurations of Internal Walls on the Threshold Value of Operation Hours for Intermittent Heating Systems
Abstract
:1. Introduction
2. Model Setup and Validation
2.1. Computational Domain
2.2. Governing Equations
2.3. Numerical Aspects and Boundary Conditions
2.4. Grid Independency
2.5. Model Validation
2.6. Study Cases
3. Results and Discussion
3.1. Comparison of Surface Temperature of Four Internal Wall Configurations
3.2. Comparison of Surface Heat Flow of Four Internal Walls
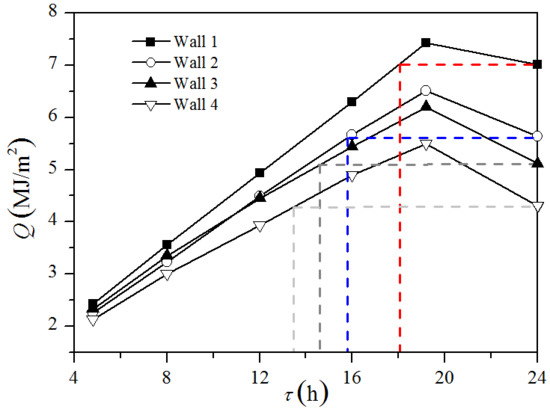
3.3. Threshold Value of Daily Operation Hours Under Four Internal Wall Configurations
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
Nomenclature
| Cp | Specific heat capacity of air (J/(kg⋅°C)) |
| Prt | Turbulent Prandtl number |
| Tu | Turbulence intensity at the inlet (%) |
| ReL | Reynolds number at the inlet |
| k0 | Turbulent kinetic energy (m2/s2) |
| V | Local air velocity (m/s) |
| T | Local air temperature (°C) |
| Tr | Reference temperature (°C) |
| To | Outdoor air temperature (°C) |
| Ti | Indoor air temperature (°C) |
| p | Power of heating device (kW) |
| l | Length scale (m) |
| y+ | Non-dimensional distance |
| Tin,i | Inner surface temperature of the internal wall (°C) |
| Tin,o | Outer surface temperature of the internal wall (°C) |
| hi | Heat transfer coefficient of inner surface of the internal wall (W/(m2⋅°C)) |
| ho | Heat transfer coefficient of outer surface of the internal wall (W/(m2⋅°C)) |
| V0 | Volume of the investigated room (m3) |
| n | Air change rate of infiltration (h−1) |
| F | Floor area of the room (m2) |
| Qi | Heating load index of room (W/m2) |
| Q | Daily heating load (MJ/m2) |
| qi | Inner surface heat flow of internal wall (W) |
| qo | Outer surface heat flow of internal wall (W) |
| Greek symbols | |
| p | Air density (kg/m3) |
| λ | Thermal conductivity (W/(m⋅°C)) |
| τo | Heating duration per operation (h) |
| τ | Hours contained in a heating cycle (h) |
| ν | Kinematic viscosity (m2/s) |
| νt | Turbulent eddy viscosity (m2/s) |
| δij | Kronecker delta |
| εr,m,s | Root-mean-square error in temperature |
| η | Increasing rate (%) |
References
- Yoshino, H.; Yoshino, Y.; Zhang, Q.; Mochida, A.; Li, N.; Li, Z.; Miyasaka, H. Indoor thermal environment and energy saving for urban residential buildings in China. Energy Build. 2006, 38, 1308–1319. [Google Scholar] [CrossRef]
- Hu, T.; Yoshino, H.; Jiang, Z. Analysis on urban residential energy consumption of Hot Summer & Cold Winter Zone in China. Sustain. Cities Soc. 2013, 6, 85–91. [Google Scholar]
- Guo, S.; Yan, D.; Peng, C.; Cui, Y.; Zhou, X.; Hu, S. Investigation and analyses of residential heating in the HSCW climate zone of China: Status quo and key features. Build. Environ. 2015, 94, 532–542. [Google Scholar] [CrossRef]
- Yu, J.; Yang, C.; Tian, L. Low-energy envelope design of residential building in hot summer and cold winter zone in China. Energy Build. 2008, 40, 1536–1546. [Google Scholar] [CrossRef]
- Code for Thermal Design of Civil Building; The People’s Republic of China National Standard GB 50176-2016; China Architecture and Building Press: Beijing, China, 2016. (In Chinese)
- Yoshino, H.; Guan, S.; Lun, Y.F.; Mochida, A.; Shigeno, T.; Yoshino, Y.; Zhang, Q.Y. Indoor thermal environment of urban residential buildings in China: Winter investigation in five major cities. Energy Build. 2004, 36, 1227–1233. [Google Scholar] [CrossRef]
- Hu, S.; Yan, D.; Cui, Y.; Guo, S. Urban residential heating in hot summer and cold winter zones of China-Status, modeling, and scenarios to 2030. Energy Policy 2016, 92, 158–170. [Google Scholar] [CrossRef]
- Le, J.; Heiselberg, P. Energy flexibility of residential buildings using short term heat storage in the thermal mass. Energy 2016, 111, 991–1002. [Google Scholar]
- Badran, A.A.; Jaradat, A.W.; Bahbouh, M.N. Comparative study of continuous versus intermittent heating for local residential building: Case studies in Jordan. Energy Convers. Manag. 2013, 65, 709–714. [Google Scholar] [CrossRef]
- Tsilingiris, P.T. Wall heat loss from intermittently conditioned space-The dynamic influence of structural and operational parameters. Energy Build. 2006, 38, 1022–1031. [Google Scholar] [CrossRef]
- Meng, X.; Luo, T.; Gao, Y.; Zhang, L.; Huang, X.; Hou, C.; Shen, Q.; Long, E. Comparative analysis on thermal performance of different wall insulation forms under the air-conditioning intermittent operation in summer. Appl. Therm. Eng. 2018, 130, 429–438. [Google Scholar] [CrossRef]
- Zhang, L.; Luo, T.; Meng, X.; Wang, Y.; Hou, C.; Long, E. Effect of the thermal insulation layer location on wall dynamic thermal response rate under the air-conditioning intermittent operation. Case Stud. Therm. Eng. 2017, 10, 79–85. [Google Scholar] [CrossRef]
- Yuan, L.; Kang, Y.; Wang, S.; Zhong, K. Effects of thermal insulation characteristics on energy consumption of buildings with intermittently operated air-conditioning systems under real time varying climate conditions. Energy Build. 2017, 155, 559–570. [Google Scholar] [CrossRef]
- ANSYS FLUENT, 14.0 Theory Guide; ANSYS: Canonsburg, PA, USA, 2011.
- Gebremedhin, K.G.; Wu, B.X. Characterization of flow field in a ventilation space and simulation of heat exchange between cows and their environment. J. Therm. Biol. 2003, 28, 301–319. [Google Scholar] [CrossRef]
- Coussirat, M.; Guardo, A.; Jou, E.; Egusquiza, E.; Cuerva, E.; Alavedra, P. Performance and influence of numerical sub-models on the CFD simulation of free and forced convection in double-glazed ventilated façades. Energy Build. 2008, 40, 1781–1789. [Google Scholar] [CrossRef]
- Rohdin, P.; Moshfegh, B. Numerical predictions of indoor climate in large industrial premises. A comparison between different k-ε models supported by filed measurements. Build. Environ. 2007, 42, 3872–3882. [Google Scholar] [CrossRef]
- Meng, X.; Yan, B.; Gao, Y.; Wang, J.; Zhang, W.; Long, E. Factors affecting the in situ measurement accuracy of the wall heat transfer coefficient using the heat flow meter method. Energy Build. 2015, 86, 754–765. [Google Scholar] [CrossRef]
- Ozel, M. Thermal performance and optimum insulation thickness of building walls with different structure materials. Appl. Therm. Eng. 2011, 31, 3854–3863. [Google Scholar] [CrossRef]
- Casalegno, A.; Antonellis, S.D.; Colombo, L.; Rinaldi, F. Design of an innovative enthalpy wheel based humidification system for polymer electrolyte fuel cell. Int. J. Hydrogen Energy 2011, 36, 5000–5009. [Google Scholar] [CrossRef]
- Ye, X.; Kang, Y.; Zuo, B.; Zhong, K. Study of factors affecting warm air spreading distance in impinging jet ventilation rooms using multiple regression analysis. Build. Environ. 2017, 120, 1–12. [Google Scholar] [CrossRef]
- Ministry of Housing and Urban-Rural Development of the People’s Republic of China. Design Standard for Energy Efficiency of Residential Buildings in Hot Summer and Cold Winter Zone (JGJ134-2010); China Architecture and Building Press: Beijing, China, 2010. (In Chinese)
- ANSYS FLUENT 14.0 User’s Guide; ANSYS: Canonsburg, PA, USA, 2011.
- Hussain, S.; Oosthuizen, P.H.; Kalendar, A. Evaluation of various turbulence models for the prediction of the airflow and temperature distributions in atria. Energy Build. 2012, 48, 18–28. [Google Scholar] [CrossRef]
- Ye, X.; Zhu, H.; Kang, Y.; Zhong, K. Heating energy consumption of impinging jet ventilation and mixing ventilation in large-height space: A comparison study. Energy Build. 2016, 130, 697–708. [Google Scholar] [CrossRef]
- Lin, B.; Wang, Z.; Liu, Y.; Zhu, Y.; Ouyang, Q. Investigation of winter indoor thermal environment and heating demand of urban residential buildings in China’s hot summer-cold winter climate region. Build. Environ. 2016, 101, 9–18. [Google Scholar] [CrossRef]











| Material | Density ρ (kg/m3) | Specific Heat Capacity c [J/(kg⋅°C)] | Thermal Conductivity λ [W/(m⋅°C)] | Thermal Storage S [W/(m2⋅°C)] | Thermal Diffusivity α [m2/s] |
|---|---|---|---|---|---|
| Plaster layer | 1700 | 1050 | 0.87 | 10.75 | 4.87 × 10−7 |
| Reinforced concrete | 2500 | 920 | 1.74 | 17.2 | 7.57 × 10−7 |
| Thermal mortar | 600 | 1050 | 0.18 | 2.87 | 2.86 × 10−7 |
| Aerated concrete block | 700 | 1050 | 0.18 | 3.10 | 2.45 × 10−7 |
| XPS | 35 | 1380 | 0.036 | 0.32 | 7.45 × 10−7 |
| Internal Wall Configuration | Thermal Resistance R [m2⋅°C/W] | Thermal Diffusivity α [m2/s] |
|---|---|---|
| Wall 1 | 0.15 | 6.89 × 10−7 |
| Wall 2 | 0.48 | 3.16 × 10−7 |
| Wall 3 | 1.15 | 2.30 × 10−7 |
| Wall 4 | 1.26 | 1.12 × 10−7 |
| Operation Case | Heating Duration per Operation τo (h) | Hours Contained in a Heating Cycle τ (h) |
|---|---|---|
| Cτ=0.5 | 0.5 h | 2.5 h |
| Cτ=1 | 1 h | 3 h |
| Cτ=2 | 2 h | 4 h |
| Cτ=4 | 4 h | 6 h |
| Cτ=8 | 8 h | 10 h |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, S.; Zhong, K. Effects of Configurations of Internal Walls on the Threshold Value of Operation Hours for Intermittent Heating Systems. Appl. Sci. 2019, 9, 756. https://doi.org/10.3390/app9040756
Wang S, Zhong K. Effects of Configurations of Internal Walls on the Threshold Value of Operation Hours for Intermittent Heating Systems. Applied Sciences. 2019; 9(4):756. https://doi.org/10.3390/app9040756
Chicago/Turabian StyleWang, Shuhan, and Ke Zhong. 2019. "Effects of Configurations of Internal Walls on the Threshold Value of Operation Hours for Intermittent Heating Systems" Applied Sciences 9, no. 4: 756. https://doi.org/10.3390/app9040756
APA StyleWang, S., & Zhong, K. (2019). Effects of Configurations of Internal Walls on the Threshold Value of Operation Hours for Intermittent Heating Systems. Applied Sciences, 9(4), 756. https://doi.org/10.3390/app9040756