Coordination of Power-System Stabilizers and Battery Energy-Storage System Controllers to Improve Probabilistic Small-Signal Stability Considering Integration of Renewable-Energy Resources

Featured Application

Power-system-controller tuning.

Abstract

This paper proposes a probabilistic method to obtain optimized parameter values for different power-system controllers, such as power-system stabilizers (PSSs) and battery energy-storage systems (BESSs) to improve probabilistic small-signal stability (PSSS) considering stochastic output power due to wind- and solar-power integration. The proposed tuning method is based on a combination of an analytical method that assesses the small-signal-stability margin, and an optimization technique that utilizes this statistical information to optimally tune power-system controllers. The optimization problem is solved using a metaheuristic technique known as the firefly algorithm. Power-system stabilizers, as well as sodium–sulfur (NaS)-based BESS controllers with power-oscillation dampers (termed as BESS controllers) are modeled in detail for this purpose in DIGSILENT. The results show that the sole use of PSSs and BESS controllers is insufficient to improve dynamic stability under fluctuating input power due to the integration of renewable-energy resources. However, the proposed strategy of using BESS and PSS controllers in a coordinated manner is highly successful in enhancing PSSS under renewable-energy-resource integration and under different critical conditions.

1. Introduction

Renewable energy can provide an inexhaustible and clean source of energy, with wind-turbine generation (WTG) and photovoltaic generation (PVG) being the two most popular forms for the conversion of clean energy [1]. However, power fluctuations due to renewable energy sources (RES) generally have a detrimental effect on small-signal stability (SSS), and can be conveniently studied using probabilistic methods [2,3,4,5]. Small-signal stability is related to the occurrence of low frequency oscillations (typically from 0.2 to 3 Hz) in the power flow between lines that can limit power-transfer capabilities, and can even lead to blackouts in the power system [6,7]. In References [2,3,4], the authors studied the effect of off- and onshore wind farms on dynamic stability, and proposed an analytical method based on cumulant and Gram–Charlier expansion to assess probabilistic SSS (PSSS). The researchers’ result showed that wind fluctuations have a probability of making a system’s small signal unstable. However, the authors constructed a probability density function (PDF) of wind-output power using a wind speed vs. power curve, which has discontinuities and is difficult to use in analytical techniques [5]. Thus, there was a need to develop a simple and accurate probabilistic model for wind-output power. The effect of PVG considering fluctuations on SSS was studied in References [8,9,10]. Unlike wind, solar energy has less variability but higher uncertainty. Thus, it is also important to analyze its effects on power-system stability. In References [8,9], the effects of stochastic fluctuations due to PVG on PSSS in a distribution network were studied. The authors found that PVG has the potential to deteriorate small-signal stability. The impact of PVG using real measured data on a large transmission system was studied in Reference [10], where the authors concluded that stochastic fluctuation due to solar irradiance can greatly hamper dynamic stability. Consequently, there is much need to study the combined effect of the two intermittent renewable sources on PSSS.

Power-system stabilizers (PSSs) are generally selected as the first option to improve SSS as they can be conveniently located at generating stations. However, other power-system devices, such as flexible AC transmission systems (FACTS), and wind and solar farms incorporating power-oscillation dampers (PODs), can also enhance low-frequency stability [7,11,12]. In recent times, as a result of its plummeting cost, research efforts on utilizing battery energy-storage systems (BESSs) to provide different power-system functions, such as frequency regulation, power-quality improvement, and oscillation damping have also gained wide popularity [13]. BESS are usually equipped with POD (termed as BESS controllers in this paper) when they are employed for oscillation damping [14,15]. They can directly modulate real output power, making them more suitable for oscillation damping compared to PSS and FACTS devices [14]. As the placement of energy-storage devices is very flexible compared with RES, it is easier to install them at locations where the controllability index to damp oscillation is highest, making it a more efficient candidate than RES with POD to improve SSS [16]. There are some recent studies in the literature that analyze the effect of BESS on low-frequency oscillatory stability [17,18]. The effect of BESS on dynamic stability with high penetration of solar and wind farms was investigated in Reference [17]. The authors observed that the tuning of a BESS controller is extremely crucial, and improper tuning may result in oscillatory instability. In Reference [18], the output power of multiple BESSs was coordinated using particle-swarm optimization (PSO) to enhance dynamic stability. The method proposed by References [17,18] provides extensive information about the enhancement of oscillatory stability using a single or multiple BESS(s). However, this approach of only utilizing PSS or BESS may not be sufficient to enhance low-frequency stability, especially under current large-scale RES integration. Thus, it is imperative to study more effective solutions, such as the coordination between PSS and BESS controllers.

As RES output power varies stochastically, this leads to a change in the operating point of a power system, creating multiple operating conditions. The controllers developed using deterministic techniques may not guarantee satisfactory operating performance under these conditions, as they were developed for single or very few operating points [19,20]. There are few researchers who have considered controller tuning by directly considering these factors [11,19,20,21,22]. Coordination between WTG incorporating PODs, and PSSs utilizing PSO, was found to be highly successful in damping low-frequency oscillations under wind uncertainty in Reference [11]. In Reference [19], PSS parameters were tuned using differential evolution techniques considering generation and load uncertainties. The tuned PSSs were found to be effective in improving dynamic stability under multiple operating conditions. In Reference [20], the design of probabilistically robust PSS controllers with wide-area signals to improve dynamic stability under wind-power fluctuations was proposed. The so-designed wide-area-based PSSs were found to be effective in improving SSS under different scenarios. The authors in Reference [21] proposed an optimal tuning method for PSSs and FACTS controllers that greatly improves PSSS. However, the authors’ technique was based on a Monte Carlo simulation, which has very high computational time. A modified fruit-fly algorithm was used for coordinating PSSs and a static-var compensator (SVC) to improve SSS under wind-power fluctuations in Reference [22]. The proposed strategy is based on a computationally efficient method that optimizes the controller parameters in considerably less time. However, all the mentioned studies in the literature tuned the controllers by considering the same renewable-energy resources [11,20,21,22] or only load uncertainty [19]. As can be seen from before the mentioned descriptions, different metaheuristic techniques were applied to optimally tune power-system controllers considering power-system uncertainties. We chose a metaheuristic technique known as the firefly algorithm for our study. The firefly algorithm is a swarm-intelligence method based on flashing patterns and the behavior of tropical fireflies. It is simple, flexible, easy to implement, and provides better convergence in less computation time compared to other nature-inspired optimization techniques, such as the genetic algorithm and PSO [23,24].

Thus, in this paper, we address the research gaps that exist in the current literature, as described in the preceding paragraphs. The major contributions of this paper are:

• Proposal of a procedure to compute the continuous probability function of RES and use it to assess PSSS.
• Development of a probabilistic method to optimally tune power-system controllers, such as PSSs and BESSs, considering power fluctuation due to RES.
• Development of a detailed model of BESSs in DIGSILENT [25], and the study of the effect of the proposed control strategy of utilizing BESS controllers and PSS in a coordinated manner on probabilistic low-frequency oscillatory stability.
• Use of the firefly algorithm to coordinate power-system controllers.

Thus, the novel contribution of our study is the proposal of a probabilistic method to tune power-system controllers, such as PSSs and BESSs controllers, considering stochastic power fluctuation arising due to two popular RES. The proposed method can be divided into two stages: Stage 1, which computes statistical information about the effect of RES integration on SSS, and Stage 2, which uses this knowledge to coordinate the power-system controllers. As the proposed method uses a probabilistic method, it is first necessary to model the input uncertainties (RES output power); however, as stated earlier, and is discussed in detail in subsequent sections, most probabilistic models of RES either contain discontinuous terms or are incomplete, which makes them difficult to use in probabilistic analysis. Thus, we also propose a procedure to obtain a probabilistic RES model that is continuous and can be conveniently applied with probabilistic methods related to the power system. Lastly, as mentioned in the preceding paragraphs, the modern electric grid continues to integrate huge amount of RES, and the sole use of PSS and BESS controllers may be insufficient to improve the SSS margin. Thus, we also propose a strategy to use PSS and BESS controllers in a coordinated manner and study their effect on PSSS. BESSs, along with controllers, are modeled in detail in DIGSILENT for this purpose.

The paper is organized as follows: Section 2 discusses the proposed method to enhance PSSS, followed by the PSSS assessment method in Section 3. Section 4 describes different power-system controllers utilized in this paper to enhance dynamic stability, as well as the optimization method to tune them. The detailed results and discussion under different scenarios are provided in Section 5. Conclusions drawn are described in Section 6.

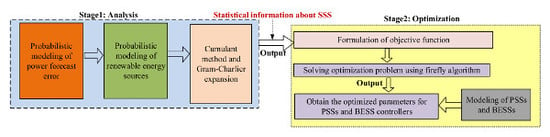
2. General Overview of the Proposed Method

The proposed method to tune power-system controllers considering stochastic power fluctuations due to RES integration is shown in Figure 1, and is a combination of two main parts: Part 1, which calculates the statistical SSS information, and Part 2, which utilizes this information to enhance oscillatory stability by coordinating different power-system controllers, such as PSS and BESS controllers, with the help of the optimization technique. The overall proposed methodology can be described as follows:

• Probabilistic modeling of input random variables (RES output power) using power-forecast error. The so-obtained probabilistic models are efficient and convenient to use with analytical methods, and are described in detail in Section 3.1.
• Input PDFs are then used with an analytical method based on cumulants [2,26] to calculate the PDF of output random variables. Output random variables in this paper are the real eigenvalue part (also called the damping constant) and damping factor. The cumulant method was chosen over other analytical methods, such as point estimate and probabilistic collocation, due to its higher accuracy as well as computational efficiency [27].
• Next, the Gram–Charlier expansion method [26] was used with output random variables to calculate statistical indices that provide information about the small-signal stability margin. More details for Steps 2 and 3 can be found in Section 3.2.
• If the system is found to have a critical value of indices with respect to oscillatory stability, the power-system controllers are then tuned in a coordinated manner. This coordination is achieved by formulating it as an optimization problem. The objective function of this optimization problem consists of probabilistic stability indices (obtained from Part 1) and is solved using the firefly algorithm. The detailed description of this process can be found in Section 4.2.

Moreover, constraints of this optimization problem are the different parameters of power-system controllers, and solving the optimization problem provides optimized value for the controller parameters. All controllers, such as PSS and BESS controllers, were modeled in great detail and can be found in Section 4.1.

3. PSSS Assessment Using Developed Efficient Probabilistic RES Model

3.1. Development of PVG Probability Function and WTG Output Power

PVG output power increases with solar radiation until it reaches standard solar radiation (around 1000 W/m${}^2$), beyond which it remains constant at its rated capacity, as shown in Figure 2 [28]. Moreover, output power from a solar farm is zero at night time. These two situations cause discontinuities in the PDF of PVG output power when it is computed using the general procedure, and are usually modeled as impulse functions, as shown in Figure 2 [2,3]. To avoid these discontinuities, researchers [8,9,10] commonly only use the linear region (where solar radiation is greater than zero and less than standard radiation) to compute the PDF of the PVG output power, which results in a continuous function and is much more convenient to use. However, the realistic probabilistic model of PVG output power should be a mixed random variable with two impulse functions, and a continuous function between them. However, this model is difficult to use with analytical methods, and a more efficient method based on power-forecast error to construct the probability density of PVG output power was utilized in our study.

Both solar-power and wind-power forecast errors are commonly modeled as normal distribution, and vary with feed-in power as well as the time of day [29,30]. Power-forecast error $\Delta P_{m,pv}$ for an $m^{th}$ solar farm is defined as

$$\Delta P_{m,pv}=P_{m,pv}-{\overline{P}}_{m,pv}$$

(1)

where $P_{m,pv}$ is actual output power for solar farm $m^{th}$, and ${\overline{P}}_{m,pv}$ is the forecast output power of the solar farm, which is deterministic (average solar-farm output power [29] in this paper). The probability function of the power-forecast error can be computed as:

$$f(\Delta P_{m,pv})=\frac{1}{{\sigma }_{\Delta P_{m,pv}}\sqrt{2\pi }}exp-\frac{{[\Delta P_{m,pv}-{\mu }_{\Delta P_{m,pv}}]}^2}{2{\sigma }_{\Delta P_{m,pv}}^2}$$

(2)

where ${\mu }_{\Delta P_{m,pv}}$ and ${\sigma }_{\Delta P_{m,pv}}$ are the mean and standard deviation of solar-power-forecast error, respectively.

Thus, the output-power PDF for the $m^{th}$ solar farm can be derived using Equations (1) and (2) with the help of a transformation:

$$f\left(P_{m,pv}\right)=\frac{1}{{\sigma }_{\Delta P_{m,pv}}\sqrt{2\pi }}exp-\frac{{[P_{m,pv}-({\overline{P}}_{m,pv}+{\mu }_{\Delta P_{m,pv}})]}^2}{2{\sigma }_{\Delta P_{m,pv}}^2}$$

(3)

As wind-power-forecast error is also commonly modeled as normal distribution [5,29,30], the output-power PDF for the $n^{th}$ wind farm can also be derived in a similar manner to PDF computation of PVG output power as:

$$f\left(P_{n,w}\right)=\frac{1}{{\sigma }_{\Delta P_{n,w}}\sqrt{2\pi }}exp-\frac{{[P_{n,w}-({\overline{P}}_{n,w}+{\mu }_{\Delta P_{n,w}})]}^2}{2{\sigma }_{\Delta P_{n,w}}^2}$$

(4)

where ${\overline{P}}_{n,w}$, ${\mu }_{\Delta P_{n,w}}$ and ${\sigma }_{\Delta P_{n,w}}$ are the forecast output power of the wind farm, which is deterministic (average wind-farm output power [29] in this paper), and mean and standard deviation of wind-power-forecast error respectively.

Both Equations (3) and (4) are continuous and very convenient to use with analytical methods. The graphical illustration of PDF computation of PVG output power using solar-power-forecast error is shown in Figure 3. Beta distribution is commonly used to characterize solar radiation and has some value of shape parameters a and b depending on location [31]. These shape parameters are then used to estimate average solar radiation $\overline{S}$, which is further used to compute the average PVG output power with the help of solar-farm power characteristics [28] in our work. Finally, the PDF of PVG output power is obtained by substituting the value of computed average PVG output power into Equation (Figure 3). The probability-density function of WTG output power can also be obtained in a similar manner, with the only exception being that Weibull distribution is commonly used to characterize wind velocity [31].

3.2. Stability Index Calculation

Let ${\lambda }_o={\alpha }_o+j{\omega }_o$ denotes the $o^{th}$ eigenvalue of the power system with real part ${\alpha }_o$ and imaginary part ${\omega }_o$. Damping factor ${\xi }_o$ can be calculated as [32]:

$${\xi }_o=\frac{-{\alpha }_o}{\sqrt{{\alpha }_o^2+{\omega }_o^2}}$$

(5)

Damping constant and damping factor are taken as output random variables in this paper, and their PDFs are calculated using the combined method of cumulant and Gram–Charlier expansion technique [2,26]. The following stability indices are then defined, which provides information about the SSS margin [22]:

$$\begin{array}{c}P({\alpha }_o<{\alpha }_c)={\int }_{-\infty }^{{\alpha }_c}{f}_{{\alpha }_o}\left(x\right)dx\hfill \end{array}$$

(6)

$$\begin{array}{c}P({\alpha }_o>{\alpha }_c)=1-P({\alpha }_o<{\alpha }_c)\hfill \end{array}$$

(7)

$$\begin{array}{c}\hfill P({\xi }_o<{\xi }_c)={\int }_{-\infty }^{{\xi }_c}{f}_{{\xi }_o}\left(x\right)dx\end{array}$$

(8)

where $f_{{\alpha }_o}$ is the PDF of the damping constant for $o^{th}$ eigenvalue, ${\alpha }_c$ is the critical margin for the damping constant, ${\xi }_c$ is the critical margin for the damping factor, and $f_{{\xi }_o}$ is the damping-factor PDF for the $o^{th}$ eigenvalue. Equation (7) provides probabilistic statistical information about SSS. A high value of this index indicates a low likelihood of a system being small-signal stable and vice versa. Similarly, Equation (8) provides the damping-factor probability of the $o^{th}$ eigenvalue being less than the critical damping factor, and a lower value is desirable for this index. Both $f_{{\alpha }_o}$ and $f_{{\xi }_o}$ can be constructed with the aid of the Gram–Charlier expansion [2,26]. More rigorous details on cumulant and PSSS theory can be found in References [2,3,4,8,9,10,26,29]

4. Coordination of PSS and BESS Controllers to Enhance Oscillatory Stability Using Proposed Method

This section first discusses modeling of controllers that were utilized in our work to enhance low-frequency oscillatory stability under renewable-resource uncertainties, and the firefly algorithm, which is used for tuning these controllers.

4.1. Power-System-Controller Modeling

4.1.1. Power-System Stabilizers

PSS structure is well-established in the literature [6,32], and its primary function is to modulate excitation-system voltage to improve dynamic stability. A typical PSS connected with a $i^{th}$ generator with rotor-speed deviation as input constitutes a gain of $K_{i,pss}$, lead-lag constant with parameters $T_{1i,pss},T_{2i,pss},T_{3i,pss},T_{4i,pss}$, and a washout block with time constant $T_{i,pssw}$, as depicted in Figure 4 [6]. The values of maximum voltage $V_{max}$, minimum voltage $V_{min}$, and $T_{i,pssw}$ are 0.2 and −0.2 p.u. and 10 s, respectively [6]. The range of other PSS parameters is provided in Section 4.2.1.

4.1.2. Modeling of Sodium–Sulfur-Based BESS and Its Controllers in DIGSILENT

The schematic diagram depicting the main BESS controllers available in DIGSILENT [25] is shown in Figure 5. However, the battery model, as well as its controllers in DIGSILENT, are generic and thus suitably modified to meet our purpose, which is described in detail in the subsequent sections. Controllers can be divided into three main types: real and reactive power controllers (P-Q controllers), charge controllers, and power-oscillation damping controllers. We used a sodium–sulfur (NaS) battery among the many battery technologies in our study as it has high energy density, efficiency, and quick response time (milliseconds), making it very useful to improve functions related to power-system stability [33]. The diagram displaying the developed model of NaS-based BESS with controllers in DIGSILENT is shown in Figure 6.

4.1.2.1. Battery Model

Figure 7 shows the equivalent model of a sodium–sulphur (NaS) battery. Battery voltage varies linearly with depth of discharge (DOD), as well as affects charging and discharging resistance [34]. DOD and state of charge (SOC) can be computed as:

$$\begin{array}{c}DOD=\frac{1}{Q_{max}}{\int }_{}^{}tdt\hfill \\ SOC=1-DOD\hfill \end{array}$$

(9)

where $Q_{max}$ is the maximum battery capacity at fully charged/discharged condition $\left(Ah\right)$. Charging resistance $R_{ch}(\Omega )$ is given by [34]:

$$\begin{array}{cc}\hfill R_{ch}=& c+dDO{D}^2+eDO{D}^3+fDO{D}^4+gDO{D}^5+hDO{D}^6+iDO{D}^7+jDO{D}^8+kDO{D}^9+lDO{D}^{10}\hfill \end{array}$$

(10)

and discharging resistance $R_{dis}(\Omega )$ can be found as: [34]:

$$\begin{array}{ccc}\hfill R_{dis}=& c+dDO{D}^2+eDO{D}^3+fDO{D}^4+gDO{D}^5+\hfill & \hfill hDO{D}^6+iDO{D}^7+jDO{D}^8+kDO{D}^9\end{array}$$

(11)

where c, d, e, f, g, h, i, j, k, and l are polynomial coefficients.

Open-circuit battery voltage $V_{oc}\left(V\right)$ can be computed as [34]:

$$\begin{array}{ccc}\hfill V_{oc}=& 2.076,\hfill & \hfill DOD\le 0.56\\ & 2.076-0.00672DOD,\hfill & \hfill DOD>0.56\end{array}$$

(12)

Finally, battery output voltage $V_{batt}\left(V\right)$ for discharging mode can be calculated as:

$$V_{batt}=V_{oc}-R_{dis}{I}_b-R_{lc}{I}_b$$

(13)

and for charging mode as:

$$V_{batt}=V_{oc}+R_{ch}{I}_b+R_{lc}{I}_b$$

(14)

where $R_{lc}$ is life-cycle resistance $\Omega$, and $I_b$ is battery current A.

4.1.2.2. POD Controller for BESS

The POD structure described in References [21,35] was used in our study and has a similar structure to PSS. However, unlike most PSSs, input feedback signal for POD can be signals from remote locations, which are often more effective for oscillation damping than local signals [35].

POD structure is very similar to PSS, and is shown in Figure 8. Lead-time constants for POD at the $i^{th}$ location are $T_{1i,pod},T_{3i,pod}$, and lag-time constants are $T_{2i,pod},T_{4i,pod}$, the washout-time constant is $T_{i,podw}$, the POD gain is $K_{i,pod}$, and maximum and minimum power limits are $P_{max}$ and $P_{min}$, respectively.

Unlike most PSSs, POD input feedback signal can be signals from remote locations that are often more effective for oscillation damping than local signals [35]. It is assumed that phasor-measurement units (PMU) that provide these remote signals were installed in our test system. However, there exists finite delay while transmitting the measured signal from PMU to POD control stations, it is commonly termed as communication delay or latency [36], and is modeled as $e^{-s{T}_d}$ in our work [35]. Value of latency $T_d$ is taken as 100 ms [35].

The feedback remote signal can be any electrical variables, such as real and reactive power flow in lines, current flow in lines, bus voltages, and angular differences. Among these variables, we chose real power flow in lines $P_{line,i}$ as input for PODs, as both reactive power and bus voltage have exciter and flux-decay components, and angular differences require an additional phase lead of 90 degrees, making them less suitable for feedback control [37]. The best input (among many real power flow in lines) for each POD controller is selected using the residue method [15,20,36]. Output from POD $P_{mod}$ was chosen to modulate the real power control loop in contrast to the reactive power loop as BESSs are located at the ends of the transmission line of our test system given in Section 5.1, in which case, real power modulation is superior to reactive power modulation [38]. The values of $P_{max}$, $P_{min}$, and $T_{i,podw}$ are 0.2 and 40.2 p.u. and 10 s, respectively [6]. The range of other POD parameters used in this paper is provided in Section 4.2.1.

4.1.2.3. PQ Controller

The PQ controller has two main loops, the active-power loop and reactive-power loop. The modeling of these loops is based on decoupled control theory, where d-axis current $i_d$ controls real power, and the q-axis current $i_q$ controls reactive power [8], as shown in Figure 9. The active-power control loop has four main input signals: set point active power $P_{ref}$, actual BESS output power P, modulating signal from POD $P_{mod}$, and signal from charge controller $P_c$. The difference between the sums of $P_{ref}$, $P_{mod}$ and $P_c$ with P is passed through a simple PI controller to synthesize $i_d$. Similarly, $i_q$ is synthesized by measuring the difference between setpoint reactive-power $Q_{ref}$ with actual reactive power Q and passing it to a PI controller. $Q_{ref}$ commonly depends on the requirement for power-factor regulation, but is assumed to be zero for this paper (unity power factor).

The current reference signals from the PQ controller are then fed to the charge controller, which controls battery charging and discharging, and provides reference currents $i_{dref}$ and $i_{qref}$, which are used to generate pulse-width modulating signals to control VSC switching.

4.2. Power-System-Controller Tuning Using Optimization Technique

4.2.1. Optimization-Problem Formulation

It is generally more convenient to use standardized expectations of damping constant ${\alpha }_o^{*}$ and damping factor ${\xi }_o^{*}$ for optimization studies, which are given by [22]:

$$\begin{array}{c}\hfill {\alpha }_o^{*}=\frac{\overline{{\alpha }_o}}{{\sigma }_{{\alpha }_o}},{\xi }_o^{*}=\frac{\overline{{\xi }_o}}{{\sigma }_{{\xi }_o}}\end{array}$$

(15)

where $\overline{{\alpha }_o}$, $\overline{{\xi }_o}$, ${\sigma }_{{\alpha }_o}$, and ${\sigma }_{{\xi }_o}$ are the expected value of the $o^{th}$ damping constant, the expected value of $o^{th}$ damping factor, standard deviation of the $o^{th}$ damping constant, and standard deviation of the $o^{th}$ damping factor, respectively, and can be computed using cumulant theory described in detail in References [2,3,4,9,10]. The objective function for the optimization problem is formulated as:

$$\mathrm{minimization}\mathrm{F}=J_1\sum _{i=1}^{p}P({\alpha }_o^{*}>{\alpha }_c)+J_2\sum _{i=1}^{p}P({\xi }_o^{*}<{\xi }_c)$$

(16)

subject to [6]:

$$\begin{array}{c}0.1\le K_{i,pss},K_{i,pod}\le 50\hfill \\ 0.01\le T_{1i,pss},T_{3i,pss},T_{1i,pod},T_{3i,pod}\le 1.5\hfill \\ 0.01\le T_{2i,pss},T_{4i,pss},T_{2i,pod},T_{4i,pod}\le 0.15\hfill \end{array}$$

(17)

Equation (16) is a minimization problem, where the objective is to minimize the likelihood of standardized expectation of the damping constant being greater than ${\alpha }_c$, and the standardized expectation of the damping factor being less than ${\xi }_c$. The values of ${\alpha }_c$ and ${\xi }_c$ depend on user requirements, and were chosen as −0.1 and 0.1, respectively, for this paper [19,22]. Equation (16) can be computed using Equations (7), (8), and (15). Values for both $J_1$ and $J_2$ were chosen to be 0.5, which corresponds to providing equal weight to both objective functions. Only the electromechanical eigenvalues of the total p were considered for the optimization problem [19,22].

4.2.2. Solving Optimization Problem Using Firefly Algorithm

The firefly algorithm is one of the most popular swarm-based optimization algorithms, and its pseudocode is given below:

Algorithm 1: General pseudocode of firefly algorithm

Computation of value for objective function $f\left(x\right)$ with t decision variables $x={(x_1,x_2,\dots .x_t)}^T$   Generate initial random population for n fireflies $x_i(i=1,2,3,\dots .,n)$   Calculate light intensity $L_i$ for $x_i$ using $f\left(x_i\right)$   Define light-absorption coefficient $\gamma$   While (k < Maximum Generation)      for i = 1:n, $\mathrm{all}$ n $\mathrm{fireflies}$    for j = 1:n, $\mathrm{all}$ n $\mathrm{fireflies}$     (if Li < Lj), Move firefly i towards j; end if    Change attractiveness with distance r $\mathrm{using}$ exp−γr    Compute new solutions and update light intensity    end for j   end for i      Rank fireflies and find current global best solution $g_b$   end while

The general flowchart of utilizing the firefly algorithm to tune power0system controllers in our study is shown in Figure 10 and is briefly described as follows:

• In the first step, each control parameter $x_i$ is assigned an array of random numbers, with the total number size of fireflies $N_{pop}$ as:

  $$\begin{array}{cc}\hfill x_i=& [K_{i,pod},K_{i,pss},T_{1i,pod},T_{1i,pss},T_{2i,pod},T_{2i,pss},T_{3i,pod},T_{3i,pss},T_{4i,pod},T_{4i,pss}]\hfill \end{array}$$

  (18)
• Control parameters are then used to compute the objective function using Equation (16), whose values represent firefly light intensity. The fireflies are then sorted and accordingly ranked. The so-obtained control parameters after ranking are termed as $x_j$.
• The movement of less-bright fireflies $x_i$ to brighter fireflies $x_j$ is given by:

  $$x_i^{t+1}=x_i^t+\beta {exp}^{-\gamma r_{ij}^2}\left(x_j^t-x_i^t\right)+{\alpha }_t{\epsilon }_j^t$$

  (19)

  where $x_i^{t+1}$ is the position of the fireflies at the next iteration, $\beta$ is the attractiveness coefficient, ${\epsilon }_j^t$ is the vector of random numbers, $\gamma$ is the light-absorption constant, ${\alpha }_t$ is the randomization parameter, and $r_{ij}$ is the Cartesian distance between two fireflies.
• If the value of a control parameter exceeds its range, it is reset back to its maximum or minimum value, depending upon its nearness to the extreme value given by Equation (17).
• Continue to the next iteration until the maximum number of iterations is reached.

5. Results and Discussion

5.1. Test System

The test system is a modified IEEE 68 bus network, which is a benchmark system to study low-frequency oscillatory dynamics in power systems [39]. This system has fifteen synchronous generators, three wind farms, and three solar farms, as shown in Figure 11. Deterministic eigenvalue analysis [32] was first run to determine RES locations.

Table 1. Results of deterministic eigenvalue analysis without RES.

No.	Damping Constant	Damping Factor	Frequency (Hz)	Associated Areas
1	−0.0102	0.0450	0.3607	2, 4 and 5
2	−0.0700	0.0164	0.6792	4 and 5
3	−0.0912	0.0183	0.7922	3 and 4

shows the damping constant and damping factor of the three most critical eigenvalues obtained for the test system without any RES. The major areas associated with the critical eigenvalues are 3, 4, and 5, and a similar conclusion was also reached in Reference [39]. Thus, we decided to install RES at Areas 3, 4, and 5, which represent the worst-case scenario with respect to SSS. The countries leading the way in PVG and WTG generally have a penetration level in the range of 20%–30% [1]. By taking this fact into consideration, we assumed a 30% RES penetration level in their respective areas, resulting in the size of solar and wind farm at Areas 3, 4 and 5 being 150, 172, and 370 MVA, respectively.

All generators consist of a fast-acting static excitation system; the details of generators, excitation systems, and line parameters can be found in Reference [37]. This paper uses a DIGSILENT built-in wind-farm model that is similar to Type-3 doubly fed induction generators with a rotor-side converter [25], and the PVG model that is available in DIGSILENT [25]. WTG and PVG parameters used in this paper are provided in Appendix A. Generator 1 (G1) to Generator 12 (G12) were assumed to be equipped with PSS. Areas 3 to 5 had large power generation and inertia, so any generator outage in these areas might seriously jeopardize system frequency [40]. Hence, one BESS is assumed to be connected in Areas 3, 4, and 5. As BESSs have not yet primarily been connected for small-signal stability purposes in the current electric-power system, we used the method proposed by the authors of Reference [41], which can be used to calculate BESS size for frequency regulation; the obtained BESS size after applying this method was not optimal, but still provides realistic battery size and is better than using an arbitrary size for analysis. Moreover, we also assumed unity power-factor operation of BESSs in our study. Thus, the size of BESS located in Areas 3, 4, and 5 was 26, 60, and 75 MVA, respectively. More details about battery-capacity determination and parameters are provided in Appendix A.

5.2. Simulation Results

5.2.1. Results under Different Controller Configurations

This section describes the obtained statistical results related to the stability of critical eigenvalues (also termed as modes) for four different controller configurations: case study with no controllers (base case), case study with only PSSs, case study with only BESS controllers, and case study with the proposed strategy of using PSS and BESS controllers.

The base case was run by disconnecting all PSSs and BESSs. The obtained result using the PSSS assessment method (described in Section 3) was first compared with MCS (10,000 simulations with 95% confidence interval) to verify its accuracy. Figure 12 shows that the PDF of the most critical eigenvalue (nearest eigenvalue to origin), obtained using the analytical method, very closely resembles MCS.Furthermore, the average root mean square [26] and computation time of the analytical method were found to be 0.1731% and 72.6 s, respectively, highlighting the accuracy and computational efficiency of the analytical method.

The probabilistic stability indices obtained for all critical electromechanical modes (15 in total) under the no-controller case study are shown under the base case heading in

Table 2. Comparison of stability indices under different controller conditions using proposed method.

No.	No Controllers		PSSs		BESS Controllers		PSSs and BESS Controllers
	$\mathit{P}(\mathit{\alpha }>-\mathbf{0.1})$	$\mathit{P}(\mathit{\xi }<\mathbf{0.1})$	$\mathit{P}(\mathit{\alpha }>-\mathbf{0.1})$	$\mathit{P}(\mathit{\xi }<\mathbf{0.1})$	$\mathit{P}(\mathit{\alpha }>-\mathbf{0.1})$	$\mathit{P}(\mathit{\xi }<\mathbf{0.1})$	$\mathit{P}(\mathit{\alpha }>-\mathbf{0.1})$	$\mathit{P}(\mathit{\xi }<\mathbf{0.1})$
	$\{\%\}$	$\{\%\}$	$\{\%\}$	$\{\%\}$	$\{\%\}$	$\{\%\}$	$\{\%\}$	$\{\%\}$
1	100	100	0	95.9100	0	0	0	0
2	96.5000	100	90.6403	100	0	0	0	0
3	92.0600	100	95.4195	100	0	0	0	0
4	94.4200	100	0	0	0	100	0	0
5	0	100	0	0	0	100	0	0
.	"	"	"	"	"	"	"	"
15	0	100	0	0	0	100	0	0

. The probability of the damping constant being greater than −0.1 was very high for Modes 1 to 4 under the base case. Furthermore, the damping factor of all modes had a 100% probability of being lower than 10% for the case without controllers. Both of these values suggest that the given test system under the base case has much potential to be small-signal unstable. This result led us to investigate potential solutions for this problem.

Note in Table 2 and here afterwards in our paper, the symbol (") refers to the ditto mark. The second controller configuration only considered PSS operation and assumed all BESSs to be disconnected. The PSSs located at Generators 1 to 12 were then simultaneously tuned using the proposed method. A population size of 50 fireflies was chosen, as this size is commonly selected by most swarm-based intelligence algorithms that are used to solve optimization problems related to low-frequency stability [11,19]. The values of $\beta$, ${\alpha }_t$, and $\gamma$ were calculated from the average length of controller parameters and are shown in

Table 3. Parameters of firefly algorithm.

${\mathit{N}}_{\mathit{pop}}$	$\mathit{\beta }$	${\mathit{\alpha }}_{\mathit{t}}$	$\mathit{\gamma }$	Repeated Evaluations
50	0.4136	0.2	1	30

. The optimization algorithm was solved using Intel (R) Core (TM) i5-2400 CPU, 3.1 GHz processing speed, with 8 GB RAM, and it took 3.15 h to compute. However, as the optimization algorithm provides the stochastic output, 30 repeated evaluations were performed and the average was used for analysis in this paper [24]. All programs were written using DIGSILENT programming language [25].

Table 2, under the PSS category, shows that, except for Modes 2 and 3, there was a low likelihood that the damping constant of other modes was greater than their margin. From a damping=factor perspective, Modes 1 to 3 had high probability of being less than the critical damping value, which shows that only employing PSSs is insufficient to provide required damping under stochastic PVG and WTG penetration. However, probabilistic statistics related to SSS were much improved in the case with only-PSS connection compared with the base case. Specifically to improve Modes 1 to 3, we performed further investigations. They were found to be interarea modes that are generally difficult to improve by only using PSSs. Thus, BESS controllers were sought to improve them, which is discussed below.

The results under the BESS controller category of Table 2 were computed by assuming all three BESS controllers of the test system were connected, and all PSSs were disabled. It was first necessary to find the best feedback signal for each BESS controller before tuning them. This paper uses residue analysis for this purpose, as discussed in Section 4.1.2.2. The signal that provides the highest residue for BESS1, BESS2, and BESS3 was found to be an active power flow between Lines 45 to 51, active power flow between Lines 41 to 42, and real power flow between Lines 43 to 44, respectively. The proposed method was then used to tune the BESS controllers.

The previously risked Modes 1 to 3 in the case with only PSSs, which have a high likelihood of being small-signal unstable, have a low likelihood of being low-frequency unstable, as can be seen from Table 2 for the case with BESS controllers. However, the probability of the damping constant being greater than the critical margin, and the probability of the damping factor being lower than the critical margin for other modes (4–15) increases drastically for this controller configuration. This is largely because they are mainly local modes that cannot be effectively damped by only using BESS controllers as they use remote signals from the PMU.

The final controller configuration case considers the test system with a connection of both BESS controllers and generators (1–12) with PSS. The objective function given by Equation (16) is first solved to obtain the optimized parameters for all PSSs and POD controllers. The convergence of the objective function is shown in Figure 13, and the minimum value of 5123 was achieved in 44 iterations.

As can be seen from Table 2 under the PSS and BESS controller heading, all modes have a low probability of being small-signal unstable with respect to their margin values, showing the effectiveness of the proposed coordinating approach of utilizing PSS and BESS controllers.

In addition, we used the optimization-based tuning method (OBTM) proposed by Reference [42] to compare the effectiveness of our proposed method. The probabilistic indices related to small-signal instability are always lower with the controllers tuned using the proposed method than the compared method, as can be seen from

Table 4. Comparison of stability indices under different controller conditions using the optimization-based tuning method (OBTM).

No.	No Controllers		PSSs		BESS Controllers		PSSs and BESS Controllers
	$\mathit{P}(\mathit{\alpha }>-\mathbf{0.1})$	$\mathit{P}(\mathit{\xi }<\mathbf{0.1})$	$\mathit{P}(\mathit{\alpha }>-\mathbf{0.1})$	$\mathit{P}(\mathit{\xi }<\mathbf{0.1})$	$\mathit{P}(\mathit{\alpha }>-\mathbf{0.1})$	$\mathit{P}(\mathit{\xi }<\mathbf{0.1})$	$\mathit{P}(\mathit{\alpha }>-\mathbf{0.1})$	$\mathit{P}(\mathit{\xi }<\mathbf{0.1})$
	$\{\%\}$	$\{\%\}$	$\{\%\}$	$\{\%\}$	$\{\%\}$	$\{\%\}$	$\{\%\}$	$\{\%\}$
1	100	100	0	97.9797	0	0	0	0
2	96.5000	100	94.3965	100	0	0	0	0
3	92.0600	100	97.5650	100	0	0	0	0
4	94.4200	100	0	0	0	100	0	0
5	0	100	0	0	0	100	0	2.7340
6	0	100	0	0	0	100	0	2.2390
.	"	"	"	"	"	"	"	"
15	0	100	0	0	0	100	0	0

.

5.2.2. Comparison of Different Controller Cases Under Different Scenarios

To further demonstrate the effectiveness of the controllers tuned using the proposed method, we analyzed it under three critical scenarios, as shown in

Table 5. Details of different scenarios.

No.	Details	Applied Disturbance for Time-Domain Simulation
1	Disconnection of critical Line 53–54	Outage of Line 53–54 at 10 s
2	Increase load of the whole system by 4%	Outage of Line 53–54 at 10 s
3	Increase generation of the whole system by 4%	Outage of Line 53–54 at 10 s

.

Table 6. Stability indices under different controller conditions for Scenario 1 using the proposed method.

No.	No Controllers		PSSs		BESS Controllers		PSSs and BESS Controllers
	$\mathit{P}(\mathit{\alpha }>-\mathbf{0.1})$	$\mathit{P}(\mathit{\xi }<\mathbf{0.1})$	$\mathit{P}(\mathit{\alpha }>-\mathbf{0.1})$	$\mathit{P}(\mathit{\xi }<\mathbf{0.1})$	$\mathit{P}(\mathit{\alpha }>-\mathbf{0.1})$	$\mathit{P}(\mathit{\xi }<\mathbf{0.1})$	$\mathit{P}(\mathit{\alpha }>-\mathbf{0.1})$	$\mathit{P}(\mathit{\xi }<\mathbf{0.1})$
	$\{\%\}$	$\{\%\}$	$\{\%\}$	$\{\%\}$	$\{\%\}$	$\{\%\}$	$\{\%\}$	$\{\%\}$
1	100	100	0	98.9374	0	0	0	0
2	100	100	6.0612	100	0	0	0	0
3	96.4595	100	93.4344	100	0	0	0	0
4	98.9926	100	0	0	0	100	0	0
5	0	100	0	0	0	100	0	0
.	"	"	"	"	"	"	"	"
15	0	100	0	0	0	100	0	0

,

Table 7. Stability indices under different controller conditions for Scenario 2 using the proposed method.

No.	No Controllers		PSSs		BESS Controllers		PSSs and BESS Controllers
	$\mathit{P}(\mathit{\alpha }>-\mathbf{0.1})$	$\mathit{P}(\mathit{\xi }<\mathbf{0.1})$	$\mathit{P}(\mathit{\alpha }>-\mathbf{0.1})$	$\mathit{P}(\mathit{\xi }<\mathbf{0.1})$	$\mathit{P}(\mathit{\alpha }>-\mathbf{0.1})$	$\mathit{P}(\mathit{\xi }<\mathbf{0.1})$	$\mathit{P}(\mathit{\alpha }>-\mathbf{0.1})$	$\mathit{P}(\mathit{\xi }<\mathbf{0.1})$
	$\{\%\}$	$\{\%\}$	$\{\%\}$	$\{\%\}$	$\{\%\}$	$\{\%\}$	$\{\%\}$	$\{\%\}$
1	100	100	93.7333	100	0	0	0	0
2	100	100	98.1607	100	0	0	0	0
3	97.1333	100	0	0	0	0	0	0
4	98.5768	100	0	0	0	100	0	0
5	0	100	0	0	0	100	0	0
.	"	"	"	"	"	"	"	"
15	0	100	0	0	0	100	0	0

and

Table 8. Stability indices under different controller conditions for Scenario 3 using the proposed method.

No.	No Controllers		PSSs		BESS Controllers		PSSs and BESS Controllers
	$\mathit{P}(\mathit{\alpha }>-\mathbf{0.1})$	$\mathit{P}(\mathit{\xi }<\mathbf{0.1})$	$\mathit{P}(\mathit{\alpha }>-\mathbf{0.1})$	$\mathit{P}(\mathit{\xi }<\mathbf{0.1})$	$\mathit{P}(\mathit{\alpha }>-\mathbf{0.1})$	$\mathit{P}(\mathit{\xi }<\mathbf{0.1})$	$\mathit{P}(\mathit{\alpha }>-\mathbf{0.1})$	$\mathit{P}(\mathit{\xi }<\mathbf{0.1})$
	$\{\%\}$	$\{\%\}$	$\{\%\}$	$\{\%\}$	$\{\%\}$	$\{\%\}$	$\{\%\}$	$\{\%\}$
1	100	100	100	100	0	0	0	0
2	96.8426	100	1.0060	100	0	0	0	0
3	95.1850	100	95.5373	100	0	0	0	0
4	98.2310	100	0	0	97.8950	100	0	0
5	0	100	0	0	0	100	0	0
.	"	"	"	"	"	"	"	"
15	0	100	0	0	0	100	0	0

describe the results obtained by tuning controllers using the proposed method under different scenarios. The probabilistic indices describing SSS instability are very low without controllers, and improve a bit, particularly for Modes 1–3 in the case with connecting only BESS controllers. Furthermore, except for a few modes (1–3), the likelihood of the system being dynamically stable is high in the case of the system with only PSSs, and highest in the case of the proposed strategy of coordinating PSS and BESS controllers for all scenarios.

The statistical results obtained by tuning controllers using the compared method for different scenarios is given in

Table 9. Stability indices under different controller conditions for Scenario 1 using OBTM.

No.	No Controllers		PSSs		BESS Controllers		PSSs and BESS Controllers
	$\mathit{P}(\mathit{\alpha }>-\mathbf{0.1})$	$\mathit{P}(\mathit{\xi }<\mathbf{0.1})$	$\mathit{P}(\mathit{\alpha }>-\mathbf{0.1})$	$\mathit{P}(\mathit{\xi }<\mathbf{0.1})$	$\mathit{P}(\mathit{\alpha }>-\mathbf{0.1})$	$\mathit{P}(\mathit{\xi }<\mathbf{0.1})$	$\mathit{P}(\mathit{\alpha }>-\mathbf{0.1})$	$\mathit{P}(\mathit{\xi }<\mathbf{0.1})$
	$\{\%\}$	$\{\%\}$	$\{\%\}$	$\{\%\}$	$\{\%\}$	$\{\%\}$	$\{\%\}$	$\{\%\}$
1	100	100	3.2220	97.1100	0	0	0	0
2	100	100	2.0290	100	2.6651	0	0	0
3	96.4595	100	98.3940	100	0	0	0	0
4	98.9926	100	0	0	0	100	1.8995	0
5	0	100	0	0	0	100	0	0
.	"	"	"	"	"	"	"	"
15	0	100	0	0	0	100	0	0

,

Table 10. Stability indices under different controller conditions for Scenario 2 using OBTM.

No.	No Controllers		PSSs		BESS Controllers		PSSs and BESS Controllers
	$\mathit{P}(\mathit{\alpha }>-\mathbf{0.1})$	$\mathit{P}(\mathit{\xi }<\mathbf{0.1})$	$\mathit{P}(\mathit{\alpha }>-\mathbf{0.1})$	$\mathit{P}(\mathit{\xi }<\mathbf{0.1})$	$\mathit{P}(\mathit{\alpha }>-\mathbf{0.1})$	$\mathit{P}(\mathit{\xi }<\mathbf{0.1})$	$\mathit{P}(\mathit{\alpha }>-\mathbf{0.1})$	$\mathit{P}(\mathit{\xi }<\mathbf{0.1})$
	$\{\%\}$	$\{\%\}$	$\{\%\}$	$\{\%\}$	$\{\%\}$	$\{\%\}$	$\{\%\}$	$\{\%\}$
1	100	100	99.0866	100	0	0	0	0
2	100	100	99.3710	100	0	0	0	0
3	97.1333	100	0	0	0	0	0	2.8950
4	98.5768	100	0	0	0	100	0	0
5	0	100	0	0	0	100	0	0
.	"	"	"	"	"	"	"	"
15	0	100	0	0	0	100	0	0

and

Table 11. Stability indices under different controller conditions for Scenario 3 using OBTM.

No.	No Controllers		PSSs		BESS Controllers		PSSs and BESS Controllers
	$\mathit{P}(\mathit{\alpha }>-\mathbf{0.1})$	$\mathit{P}(\mathit{\xi }<\mathbf{0.1})$	$\mathit{P}(\mathit{\alpha }>-\mathbf{0.1})$	$\mathit{P}(\mathit{\xi }<\mathbf{0.1})$	$\mathit{P}(\mathit{\alpha }>-\mathbf{0.1})$	$\mathit{P}(\mathit{\xi }<\mathbf{0.1})$	$\mathit{P}(\mathit{\alpha }>-\mathbf{0.1})$	$\mathit{P}(\mathit{\xi }<\mathbf{0.1})$
	$\{\%\}$	$\{\%\}$	$\{\%\}$	$\{\%\}$	$\{\%\}$	$\{\%\}$	$\{\%\}$	$\{\%\}$
1	100	100	100	100	0	0	0	0
2	96.8426	100	1.8218	100	0	0	0	0
3	95.1850	100	100	100	0	0	0	0
4	98.2310	100	0	0	0	100	0	0
5	0	100	0	0	0	100	0	0
.	"	"	"	"	"	"	"	"
15	0	100	0	0	0	100	0	0

, and the system SSS margin is always less when compared with the proposed method under all scenarios.

To validate the statistical results, time-domain simulations were also run for both the proposed method and OBTM under different scenarios. Figure 14 shows the power-flow plots through critical Line 53–54, $P_{53–54}$ when a circuit is disconnected under different controller configurations (tuned using both the proposed method and OBTM) for different scenarios. $P_{53–54}$ oscillates largely without any controller, and time response improves with the separate application of PSS and BESS controllers. Furthermore, both oscillation settling time and amplitude are lowest with the proposed strategy of utilizing PSS and BESS controllers in a coordinated manner when compared with other controller configurations, thus highlighting the efficiency of the proposed control strategy. Furthermore, it can also be seen that the time response of $P_{53–54}$ following a disturbance is much better when the power-system controllers are tuned using the proposed method than with the compared method.

Overshoot [43] and settling-time [43] values for both the proposed and compared method for the time characteristics of $P_{53–54}$ are given in

Table 12. Comparison of time responses of $P_{53–54}$ using the proposed method.

Scenario	No Controllers		PSSs		BESS Controllers		PSSs and BESS Controllers
	$\mathit{OS}$$(\%)$	${\mathit{T}}_{\mathit{s}}$$\left(\mathbf{s}\right)$	$\mathit{OS}$$(\%)$	${\mathit{T}}_{\mathit{s}}$$\left(\mathbf{s}\right)$	$\mathit{OS}$$(\%)$	${\mathit{T}}_{\mathit{s}}$ (s)	$\mathit{OS}$$(\%)$	${\mathit{T}}_{\mathit{s}}$$\left(\mathbf{s}\right)$
1	-	-	5.1581	19.3900	6.8738	26.0372	5.1398	12.9783
2	-	-	5.3265	19.8046	8.1256	25.0869	5.2671	13.0508
3	-	-	4.7237	19.3348	6.1518	29.9032	4.6581	13.1429

and

Table 13. Comparison of time responses of $P_{53–54}$ using OBTM.

Scenario	No Controllers		PSSs		BESS Controllers		PSSs and BESS Controllers
	$\mathit{OS}$$(\%)$	${\mathit{T}}_{\mathit{s}}$$\left(\mathbf{s}\right)$	$\mathit{OS}$$(\%)$	${\mathit{T}}_{\mathit{s}}$$\left(\mathbf{s}\right)$	$\mathit{OS}$$(\%)$	${\mathit{T}}_{\mathit{s}}$ (s)	$\mathit{OS}$$(\%)$	${\mathit{T}}_{\mathit{s}}$$\left(\mathbf{s}\right)$
1	-	-	7.2815	22.4320	6.9164	32.0292	9.9199	20.8999
2	-	-	9.1993	20.8999	7.6818	29.7599	7.5793	18.2493
3	-	-	6.7955	27.9364	6.2899	31.2617	6.7386	17.3451

. The overshoot and settling-time values were less for all cases when controllers were tuned using the proposed method when compared to OBTM, highlighting the effectiveness of the developed method. It should be noted that scenarios without any controllers are unstable; thus, no time characteristics were calculated for them.

6. Conclusions

In this paper, an analytical method based on a combined cumulant and Gram–Charlier expansion method was used to analyze SSS under RES penetration. The results show that stochastic power fluctuation due to wind and solar farms has the potential to deteriorate low-frequency oscillatory stability. Hence, we proposed a method to optimally tune power-system controllers to improve PSSS that takes into account output-power variation from RES. The proposed method was first used to tune PSSs that were found to mostly improve local modes, but be ineffective in improving interarea modes. Furthermore, the proposed method was applied to tune POD controllers of NaS-based BESSs, and was found to be effective in mainly damping interarea modes. Finally, the effect of using the proposed strategy of utilizing both PSS and BESS controllers in a coordinated manner, whose parameters are tuned using the proposed method, was studied. This proposed strategy was observed to be highly efficient in enhancing PSSS even under stochastic power fluctuation due to RES integration. These results were also confirmed with the aid of time-domain simulation responses conducted under different scenarios. Moreover, the power-system controllers tuned using the proposed method provided a better small-signal stability margin than the compared method [42].

In future studies, better sizing and optimal BESS location will be done to improve PSSS under RES integration. The effect of variable latencies on coordinating controllers will also be studied.