1. Introduction
Characterizing the performance of communications devices in a certain frequency band can be done by discretizing the frequency band into a number of discrete points, and repeatedly characterizing the response of the device in each one of these points. However, if the response of this device is complex, many points are needed to properly characterize the response, and thus this discrete frequency sweep becomes a time consuming process.
Therefore, fast frequency sweep techniques are necessary to speed up the simulation process. A fast frequency sweep technique must provide an accurate response of the device with small error when compared with the discrete frequency sweep response, and it must do so consuming as little time as possible.
Many fast frequency sweep techniques have been proposed in the technical literature. In [
1], the asymptotic waveform evaluation (AWE) and the complex frequency hopping (CFH) techniques are both used for performing a fast frequency sweep in the analysis of substrate integrated waveguides (SIW).
In the asymptotic waveform evaluation [
2,
3,
4], the whole frequency response is approximated from the computation of the accurate response in only one single frequency point inside the bandwidth of interest. A Padé approximation to a reduced order rational polynomial is performed, and this approximation is used to interpolate over the whole frequency band with a certain degree of accuracy. The AWE technique has also been applied for the fast calculation of the radar cross-section [
5], to the solution of general mixed circuit and electromagnetic problems with a full-wave method of moments solver [
6], and to the characterization of an arbitrary two-dimensional dielectric waveguide using the tangential-vector finite-element method (TVFEM) [
7].
However, the desired bandwidth in which the device has to be characterized is frequently so wide that it is not possible to get an accurate approximation from a single point. A possible solution to this problem is to use more than one point to develop such approximation. The main drawback of this strategy is that it is difficult to find the appropriate points for these partial AWE sub-expansions. To find these points, the complex frequency hopping (CFH) technique [
8,
9] can be used. Applying this technique can guarantee that the approximation will be as good as desired. The width of the analyzed frequency range will not affect the precision of the results, but the cost will be proportionally increased, since the accurate response of the device will have to be computed in more than one discrete point (as many as necessary to obtain accurate results).
As the authors of this work already experienced when implementing the AWE and the CFH techniques in [
1], these techniques are complex and difficult to implement. Thus, a more straightforward fast frequency sweep would be desirable.
Another fast frequency sweep technique is the vector fitting technique [
10], which approximates the frequency response by a rational function and replaces a set of starting poles with an improved set of poles via a scaling procedure. This technique can approximate complex functions, but, as in the case of AWE and CFH, it also requires complex computations in order to obtain the poles of the approximated rational function.
Other fast frequency sweep techniques have also been presented, such as the balanced truncation proper orthogonal decomposition (BT-POD) [
11], which uses an adaptive frequency sampling method that allows a speed-up of 16 times when compared with discrete sweep, although this is a technique that is dependent on the electromagnetic solver, and can only be used in conjunction with the BT-POD. The same happens with the fast sweep technique presented in [
12], which presents an adaptive multi-point method that chooses several frequency points called expansion frequencies for implementing a reduced order model in a finite element solver. The methods in [
11,
12] are intrusive, requiring access to the frequency-dependent system representation.
Segmenting the structure into simple blocks is a common strategy used by many authors to speed up the analysis of complex microwave devices [
13,
14,
15,
16]. Each building block (i.e., inverters, resonant posts, empty transmission lines, etc.) is characterized by its generalized (multimode) scattering or admittance matrix, and then all these matrices are cascaded with well-known methods such as the ones presented in [
17,
18,
19,
20]. Once all the circuital matrices have been cascaded, a global circuital matrix that characterizes the whole structure, is obtained. The segmentation procedure is independent of the electromagnetic solver used for the characterization of each building block. Even different solvers can be used for characterizing different individual building blocks.
In this work, we present a simple, non-intrusive, and solver independent fast frequency sweep technique, which takes profit of the segmentation of the structure under analysis into simple constitutive blocks. Each one of these simple blocks typically presents a simple frequency response that can be easily interpolated with very few frequency points.
In [
1], the structure was already segmented into simple blocks. However, the fast frequency sweep (either using AWE or CFH) was applied to the complex and quickly changing frequency response of the whole filter. Thus, if the device was a filter with a high number of cavities, the frequency response became more complex, and the approximation with only one frequency point with AWE became less accurate. Thus, CFH needed to be used, and the number of sub-domains and frequency points where the exact solution had to be computed increased with the complexity of the frequency response (i.e., with the number of filter cavities). The same would have happened if vector fitting would have used.
In this work, a different strategy is proposed. The idea is to take profit of the fact that the individual building blocks (inversors, empty lines, resonant posts, etc.) have simple frequency responses regardless of the number of building blocks that compose the whole structure, and therefore regardless of the complexity of the frequency response of the whole device. Thus, the strategy consists of applying a simple fast frequency sweep scheme, such as spline interpolation, to the computation of the frequency response of each one of the elements of the multimodal circuital matrix. Thus, an approximated, but very accurate, mutimodal circuital matrix of each building block is obtained in as many frequency points as desired. Finally, all these matrices are cascaded, and the scattering parameters of the whole device is obtained. With this procedure, the total simulation time is significantly reduced.
To the best knowledge of the authors, this is the first time that the segmentation of the structure into simple building blocks is used to implement a fast frequency sweep. The result is a technique that can be applied to accelerate any simulation technique; that is not intrusive, and thus does not require access to the frequency dependent part of the simulator; and that is simple to implement, regardless of the complexity of the whole frequency response of the device, since the simple building blocks will always present simple frequency responses.
To test the performance of this new fast frequency sweep technique, it was applied to the computation of the frequency response of several devices: an all-metallic coupled cavities filter in rectangular waveguide, a coupled cavities filter in rectangular waveguide with dielectric posts loading each resonator, and finally a coupled cavities filter in substrate integrated waveguide (SIW). These devices were selected to have a wide variety of possible simple building blocks (irises, dielectric posts, and metallic vias), in order to ensure that the method produces good results in all cases. All this type of building blocks present simple frequency responses, but some simpler than others. Thus, depending on the building block, a different (but small in all cases) number of points (three, four or five) was used for the spline interpolation of the frequency response of the building blocks. In all cases, an accurate result with very little computational cost was obtained.
2. Fast Sweep with Segmentation and Spline Interpolation
To perform the fast sweep, we use an electromagnetic solver to compute the multimodal circuital matrix of each building block in a reduced number of frequency points. Let be the scattering parameter of a given building block that relates the mth mode accessing the building block by the jth access port and the nth mode exiting by the ith access port. Let with be the frequency points where the electromagnetic solver is used to accurately compute the scattering parameters of each building block.
Therefore, the value of is known in P points along the operational frequency band. is not a very complex function since it characterizes a simple building block. Now, the problem is to accurately interpolate this function and estimate its value in any point inside the frequency band. In this work, we have chosen the cubic spline in order to perform the interpolation.
In mathematics, a spline [
21] is a special function defined piecewise by polynomials. To per form the interpolation, splines are preferred to the use of a single polynomial for all the domain because they yield similar results when using low degrees, and they avoid the Runge’s phenomenon of oscillations at the edges that happens with polynomials for high degrees. Another advantages of splines are the ease of representation and computation.
Among all splines, the cubic spline [
22] is the most frequently used due to the optimum compromise between accuracy and simplicity, so this is the choice adopted in this work. Let
be the spline function that interpolates and approximates
. Therefore,
is defined as a different cubic polynomial in each interval
. Let
be the cubic polynomial that represents
in the interval
.
Each piece
(
) of
is defined as a cubic polynomial of the form
where
The coefficients
(
) are
P unknowns that must be determined. To do so, the first and second derivatives of the cubic polynomials are derived
The continuity of the first derivatives of each pair of contiguous cubic polynomials is ensured due to the way the cubic polynomials have been defined, since .
To determine the value of the coefficients
, the continuity of the second derivatives of each pair of contiguous cubic polynomials is enforced
This gives the following
equations
Two more equations are still needed to determine the
P unknowns. In the case of
natural splines, the choice is to enforce that the second derivative at the extremes of the interpolation domain be zero, that is
which gives the following two equations
The
equations of Equation (
10) and the two equations of Equation (
13) constitute a linear system of
P equations with
P unknowns. The solution of this system are the coefficients
(
). With those coefficients, all the cubic polynomials
are completely determined, and the approximation
of the element
of the generalized scattering parameter, as defined in Equation (
1), is accomplished using only the information of
P discrete frequency points.
The number of discrete points
P used to approximate the response of each building block depends on the complexity of the block. As shown in
Section 5, even with complex building blocks, such as a resonant post, it is enough to use only five points (
). With simpler building blocks,
P can be even smaller. This small number of points is possible even for long and complex devices, such as coupled cavities filters with many resonant cavities, thanks to the segmentation into simple building blocks and the approximation with splines of the individual response of each block, instead of approximating the response of the whole device.
3. Coupled Cavities Filter in Rectangular Waveguide
The performance of the fast frequency technique proposed in this work was first tested with the analysis of an all-metallic coupled cavities filter in rectangular waveguide technology. The layout of this filter is shown in
Figure 1. The filter was designed for a Chebyshev frequency response centered at 15 GHz, with a bandwidth of 450 MHz, and a ripple of 0.02 dB in the pass band. To test the accuracy and speed of the fast frequency technique for different sizes of the whole device, the filter was designed for different numbers of resonators
R, with
R varying within 3–9.
R = 3: w = w = 8.314 mm, w = w = 5.787 mm, l = l = 9.990 mm, l = 11.201 mm
R = 4: w = w = 8.178 mm, w = w = 5.551 mm, w = 5.124 mm, l = l = 10.152 mm, l = l = 11.503 mm
R = 5: w = w = 8.114 mm, w = w = 5.457 mm, w = w = 4.959 mm, l = l = 10.217 mm, l = l = 11.581 mm, l = 11.733 mm
R = 6: w = w = 8.072 mm, w = w = 5.404 mm, w = w = 4.887 mm, w = 4.813 mm, l = l = 10.258 mm, l = l = 11.618 mm, l = l = 11.793 mm
R = 7: w = w = 8.043 mm, w = w = 5.370 mm, w = w = 4.850 mm, w = w = 4.753 mm, l = l = 10.285 mm, l = l = 11.639 mm, l = l = 11.818 mm, l = 11.845 mm
R = 8: w = w = 8.030 mm, w = w = 5.349 mm, w = w = 4.829 mm, w = w = 4.725 mm, w = 4.703 mm, l = l = 10.298 mm, l = l = 11.652 mm, l = l = 11.832 mm, l = l = 11.866 mm
R = 9: w = w = 8.028 mm, w = w = 5.343 mm, w = w = 4.820 mm, w = w = 4.710 mm, w = w = 4.678 mm, l = l = 10.300 mm, l = l = 11.655 mm, l = l = 11.837 mm, l = l = 11.875 mm, l = 11.883 mm
To implement the fast frequency technique, the filter had to be segmented into simple building blocks, as shown in
Figure 2. In this case, these building blocks were either empty sections of rectangular waveguide (labeled as
Line i in
Figure 2) or H-plane inductive irises (labeled as
Iris i in
Figure 2). The generalized scattering matrix (GSM) of the empty line sections could be computed analytically [
23], and the GSM of the irises had to be obtained using a numerical method. In this case, the mode matching method described in [
24] was used, although any other method could also have been used. The fast frequency sweep procedure was not affected by the particular choice of analysis methods used for computing the scattering matrices of the building blocks, thus its performance would be the same if other simulators were used for obtaining these matrices. The GSM matrix of each building block had to be multimodal, because high order modes were excited inside each building block and they were not completely attenuated (and cannot be discarded) at the reference planes, which were located very near to the adjacent building blocks. Thus, the GSM elements were
, with two accessing ports (i.e., with
), and with
N and
M modes considered at the input and output ports (
,
). For the analysis of the coupled cavities filter,
was chosen to produce accurate results.
First, the GSM of the building blocks was computed using a discrete frequency sweep of
points, and next all the GSM were cascaded (using, for example, the method in [
20]) obtaining the frequency response of the whole filter in each one of these 500 frequency points with full accuracy. This took 2.808 s for
cavities, and 5.298 s for
cavities. To implement the fast frequency sweep, the number of discrete frequency points
P had to be chosen.
P had to be as small as possible to reduce the computation time at maximum, without compromising the accuracy.
To properly choose the correct value for
P for this type of filter, the fast frequency sweep was implemented for different values of
P. This means that the GSM of each building block was computed only for
P points linearly spaced in the frequency band of interest, and then the spline approximation
of Equation (
1) was used to estimate the frequency response of each element of the GSM in the 500 frequency points of the discrete sweep. This was extremely fast since it only required the evaluation of the cubic polynomials of Equation (
2). Finally, the GSM of all the building blocks were cascaded and the GSM of the whole filter was obtained. The fast frequency sweep was implemented for different values of
P for
and for
filter cavities. Results are shown in
Table 1 and
Table 2. These tables list the computation time of the fast frequency sweep, the comparison with the computation time of the discrete sweep, and the mean squared error between the reflection coefficient of the fast and discrete sweep, computed as follows:
If
, the error was too big, and results were inaccurate. For
, the error was small enough to get very accurate results. This is because the frequency response of the irises was very flat, and it could be approximated with very few points. To illustrate this, the frequency response of some elements of the GSM for the first and second irises of the filter are plotted in
Figure 3. The real and imaginary parts of these elements computed with mode matching is depicted for the 500 discrete frequency points with solid line. For comparison, the same frequency response but approximated with splines with
is also plotted. The three points used to compute the coefficients of the cubic polynomials of the spline approximation are depicted as big blue dots. It can appreciated that the frequency response was very flat, and that the spline interpolation was highly accurate with
P as small as 3.
Table 1 and
Table 2 also prove that the fast frequency sweep required only around 15% of the computation time required by the discrete frequency sweep. This time slightly increased as
P increased, which was the reason for choosing a value of
P as small as possible without compromising the accuracy.
Figure 4 compares the discrete and fast frequency sweep responses of the whole filter with
cavities. As expected, the fast frequency response was highly accurate with
.
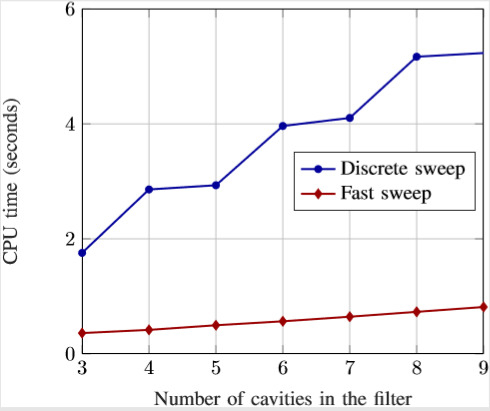
The same comparison was made for different number of filter orders. The results are shown in
Figure 5 and
Figure 6. It can be observed that the fast sweep required approximately 16% of the computation time required by the discrete sweep, even for high filter orders.
4. Coupled Cavities Filter in Rectangular Waveguide Loaded with Circular Dielectric Posts
To test the fast frequency technique with a device with more complex building blocks than in the all-metallic filter, a coupled cavities filter with dielectric resonators in rectangular waveguide was analyzed.
The geometry of the filter is shown in
Figure 7. Each resonant cavity was loaded with a cylindrical dielectric post. The dielectric posts reduced the size of the filter, at the expense of increasing the insertion losses. The filter was designed for a four-pole Chebyshev frequency response centered at 11 GHz and with a bandwidth of 300 MHz, thus the filter had four resonant cavities, and four dielectric posts.
The segmentation of the filter into simple building blocks is illustrated in
Figure 8. In this case, there were three types of building blocks. Besides sections of empty lines and irises, in this filter, there were also dielectric posts. As in the previous filter, the GSM of the empty lines were obtained analytically [
23], and the GSM of the irises were obtained with mode matching [
24]. The GSM of the dielectric posts could be computed using, for example, the hybrid mode matching method in [
25]. Here,
modes were used to compute the GSM of all building blocks.
The frequency response of the dielectric posts was not as flat as the response of the irises. For that reason, the adequate value of
P might be different from in the previous filter.
Table 3 shows the performance of the fast frequency sweep for different values of
P for the dielectric loaded filter. As can be observed, the error was bigger than in the case of the all-metallic filter. It can also be observed that the percentage of computational time of the fast sweep when compared with the discrete sweep was around 9%, which is smaller than in the all-metallic filter. This was due to the higher computational cost of the dielectric posts, which means there was a greater gain in computational cost with the fast sweep. The error was reduced as
P increased (and the computational time was slightly increased). The exact value of
P from which the results were accurate can be better derived from the results in
Figure 9. In that figure, the approximate frequency response of the element
of the GSM for the first dielectric post of the filter is depicted for different values of
P. That approximate frequency response was compared with the accurate result. It can be appreciated that the frequency response was more complex than that of the iris, and therefore in this case
points had to be used to get an accurate approximation with splines. Besides, as shown in
Table 3, the error decreased very quickly for
and
, but was stabilized for
, thus
was a good compromise between accuracy and efficiency.
Figure 10 shows the frequency response of other elements of the GSM with
, proving that with
all responses were well approximated.
Figure 11a,b shows the frequency response of the whole filter with, respectively,
and
. With four points for the spline approximation, the frequency response of the posts was not approximated with enough accuracy, and when all the GSM were cascaded and the response of the whole filter was obtained, there were differences between the discrete and the fast sweep, as can be observed in
Figure 11a. However, when
was used, the accuracy was good enough and both fast and discrete sweep were in good agreement, as shown in
Figure 11b.
5. Coupled Cavities Filter in Substrate Integrated Waveguide
Finally, the fast sweep method was tested with the analysis of a coupled-cavity filter using substrate integrated waveguide (SIW) technology [
26]. The substrate integrated waveguide was a rectangular waveguide synthesized in a dielectric substrate with circular metallic vias that acted as the lateral walls of the waveguide. The layout of the SIW filter is shown in
Figure 12. In this case, the building blocks were made of metallic vias, as depicted in
Figure 13. Some blocks were constituted by vias that form an empty SIW line, and others by vias that form a coupling iris.
The filter was designed to have a Chebyshev response centered at 11 GHz and a bandwidth of 1 GHz. The filter haf eight resonant cavities.
In this case, the GSM of the building blocks was obtained with the numerical method described in [
1], which uses a hybrid method of moments and mode matching method. Here,
modes were used.
To find the value of
P that provides with accurate results, a study was performed, as in the previous examples, of the variation of the computational time and the error between fast sweep and discrete sweep responses as a function of
P. The result is shown in
Table 4. It can be observed in this case that the computational times were significantly greater than in the previous examples, as the structure under analysis was much more complex (many metallic vias). The time reduction of the fast sweep when compared to the discrete sweep was smaller than in the first example, and similar to the second one, probably due to the greater complexity of the frequency responses of the building blocks, similar to the second example. The error was stabilized for
. Thus, this could be a good choice for
P.
However, after studying the frequency response of the building blocks, it was observed that with
the accuracy was good enough to properly approximate those responses with splines, although
could also be a good choice.
Figure 14 shows the frequency response of various elements of the GSM of various blocks. In all cases, the response was well approximated with four points. The response of the whole SIW filter for fast and discrete sweep is compared in
Figure 15. A can be observed, both responses were in good agreement, thus using four points was enough for this filter. In this case, the discrete sweep took 88 s, and the fast sweep 6.8 s. Thus, the use of the fast sweep reduced the computational time to the 7.7% of the time required by the discrete sweep.
The performance of the fast sweep technique presented in this work was compared to the performance of the previous fast sweep techniques implemented in our research group (AWE [
2] and CFH [
8]).
Figure 16 shows the reflection coefficient of the SIW filter of
Figure 12. This reflection coefficient was calculated using the three fast sweeps. It can be observed that the AWE technique approximated the response correctly near the central frequency, but it failed to do so in the extremes of the frequency band. This was because AWE used only the central point to perform the approximation, as already explained in the Introduction, and therefore was suitable only for narrow band responses. In this case, AWE had to be substituted by CFH, which segmented the frequency band into several intervals and used AWE inside each one of these intervals, thus increasing the computation time, but producing accurate results. The reflection coefficient computed with the frequency sweep of this work also provided accurate results (as proven in
Figure 15). The computational time of these three frequency sweep techniques is compared in
Table 5. The fast frequency of this work, based on segmentation, was much faster than CFH, providing equally accurate results.
6. Discussion
In this work, a new fast frequency sweep technique is presented. It consists in segmenting the device under analysis into simple building blocks, and characterizing each block with its generalized circuital matrix. Since each element of that matrix presents a simple and flat response over the frequency, it is approximated with very few points with natural cubic splines. The spline approximation provides accurate response of the block along the frequency band with as many points as desired in a very efficient way, thus saving computational time. The circuital matrices of all the blocks are then cascaded, and the scattering parameters of the whole device are finally obtained.
To test the performance of the technique with devices that contain a wide variety of possible building blocks, several types of devices were analyzed. All metallic and dielectric loaded filters in rectangular waveguide, as well as a filter in substrate integrated waveguide were analyzed. Therefore, the analyzed building blocks were empty lines, irises and dielectric posts in rectangular waveguide, as well as metallized circular vias. Depending of the block, the complexity of the frequency response differs, and a different number of points was needed for the spline approximation, but, in the worst case, it was enough to use five points.
As a result, the new fast frequency provided accurate results with a time reduction that ranged from 9% to 19%, depending on the device, when compared with the discrete frequency sweep with the same electromagnetic solver.
When compared to other fast frequency sweep techniques, such as AWE or CFH, the method of this work performed much better.
It can be concluded that, if the structure is divided into the smallest possible building blocks (such as empty lines, irises, dielectric posts, or metallic vias), the method is accurate and fast. The smaller are the building blocks, the simpler is the frequency response of each individual block, and the greater is the final accuracy using this fast frequency method. At the same time, when the building blocks are very small, their scattering matrices can be reused for the same building block appearing in another part of the structure, and the total computation time is reduced.
Although the fast frequency method was applied here to inline structures, it could also easily be applied to more complex structures such as cross-coupled filters or folded dual-mode filters. The difference is that, in those more complex structures, some individual blocks should be three- or four-port devices (such as a three port T-junction). However, even a T-junction has a simple frequency response that can be easily approximated with splines with a small number of frequency points.