A Novel Method of Hyperspectral Data Classification Based on Transfer Learning and Deep Belief Network
Abstract
:1. Introduction
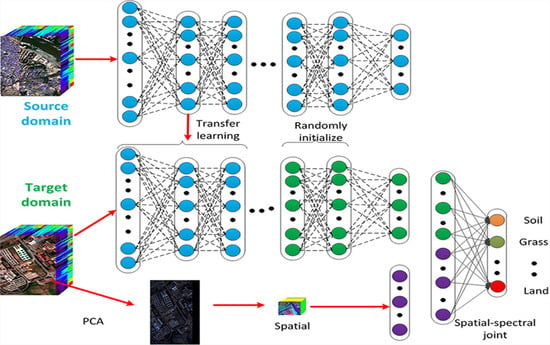
2. Algorithm
2.1. Deep Belief Network
2.2. Transfer Learning
| Algorithm 1. deep transfer learning training |
| 1: Initialize , |
| 2: Input X |
| 3: for i = 1,2, …, n; |
| 4: Train i RBM |
| 5: |
| 6: end |
| 7: If Fine tune training |
| 8: while ij Δε ≤ Threshold |
| 9: Input {X’;Y} |
| 10. Initialize |
| 11: Using Gradient Descent method |
| 12: Output (k)(k) |
| 13: end |
| 14: End |
| 15: INPUT transfer layers T |
| 16: FOR T = 1,2,3, …, n; |
| 17: Replace parameters |
| 18: Initialize |
| 19: Fine-tune network using gradient descent method; |
| 20: Output optimal results, parameter T, Output (k)(k) |
| 21: END |
3. Experiment and Parameter Selection
3.1. Experimental Data
3.2. Influence of Network Parameter
3.3. Weight Visualization
3.4. Influence of Transfer Layer
3.5. The Number of Target Domain Samples
4. Experimental Results Comparation
4.1. Spatial and Spectral Information Fusion
4.2. Comparison with Other Methods
4.3. Confusion Matrix
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Qian, S.; Hollinger, A.B.; Williams, D.J.; Manak, D. Fast three-dimensional data compression of hyperspectral imagery using vector quantization with spectral-feature-based binary coding. Opt. Eng. 1997, 35, 3242–3249. [Google Scholar] [CrossRef]
- Landgrebe, D. Hyperspectral image data analysis. IEEE Signal Process. Mag. 2002, 19, 17–28. [Google Scholar] [CrossRef]
- Cochrane, M.A. Using vegetation reflectance variability for species level classification of hyperspectral data. Int. J. Remote Sens. 2000, 21, 2075–2087. [Google Scholar] [CrossRef]
- Gao, B.C.; Montes, M.J.; Davis, C.O.; Goetz, A.F.H. Atmospheric correction algorithms for hyperspectral remote sensing data of land and ocean. Remote Sens. Environ. 2009, 113, S17–S24. [Google Scholar] [CrossRef]
- Feng-Jun, L.; Hao, Y.S.; Wang, J.; Yao, F.-J. Extraction of Alteration Mineral Information Based on Hyperspectral Data in Vegetation Covering Field. J. Jilin Univ. 2011, 41, 316–321. [Google Scholar]
- Gagnon, P.; Scheibling, R.E.; Jones, W.; Tully, D. The role of digital bathymetry in mapping shallow marine vegetation from hyperspectral image data. Int. J. Remote Sens. 2008, 29, 879–904. [Google Scholar] [CrossRef]
- Tiwari, K.C.; Arora, M.K.; Singh, D. An assessment of independent component analysis for detection of military targets from hyperspectral images. Int. J. Appl. Earth Observ. Geoinform. 2011, 13, 730–740. [Google Scholar] [CrossRef]
- Kruse, F.A. The Effects of Spatial Resolution, Spectral Resolution, and SNR on Geologic Mapping Using Hyperspectral Data, Northern Grapevine Mountains, Nevada, USA. 2000. Available online: http://ww.hgimaging.com/PDF/Kruse_AV2000.pdf (accessed on 30 March 2019).
- Robinson, I.S. Hyperspectral image dimension reduction system and method. U.S. Patent 8,538,195 B2, 17 September 2007. [Google Scholar]
- Liu, A.; Jun, G.; Ghosh, J. Active learning of hyperspectral data with spatially dependent label acquisition costs. IEEE Int. Geosci. Remote Sens. Symp. IGARSS 2009, 5, V256–V259. [Google Scholar]
- Chen, Y.R.; Cheng, X.; Kim, M.S.; Tao, Y.; Wang, C.Y.; Lefcourt, A.M. A novel integrated PCA and FLD method on hyperspectral image feature extraction for cucumber chilling damage inspection. Trans. Am. Soc. Agric. Eng. 2004, 47, 1313–1320. [Google Scholar] [CrossRef]
- Chintan, A.; Shah, M.; Arora, K. Unsupervised classification of hyperspectral data: An ICA mixture model based approach. Int. J. Remote Sens. 2004, 25, 481–487. [Google Scholar]
- Ren, H.; Chang, Y.L. Feature extraction with modified Fisher’s linear discriminant analysis. Proc. SPIE Int. Soc. Opt. Eng. Chem. Biol. Standoff Detect. 2005, 5995, 56–62. [Google Scholar]
- Hinton, G.E.; Salakhutdinov, R.R. Reducing the dimensionality of data with neural networks. Science 2006, 313, 504–507. [Google Scholar] [CrossRef] [PubMed]
- Chen, Y.; Zhao, X.; Jia, X. Spectral–Spatial Classification of Hyperspectral Data Based on Deep Belief Network. IEEE J. Sel. Top. Appl. Earth Observ. Remote Sens. 2015, 8, 2381–2392. [Google Scholar] [CrossRef]
- Chen, Y.; Lin, Z.; Zhao, X.; Wang, G.; Gu, Y. Deep learning-based classification of hyperspectral data. IEEE J. Sel. Top. Appl. Earth Observ. Remote Sens. 2014, 7, 2094–2107. [Google Scholar] [CrossRef]
- Vincent, P.; Larochelle, H.; Lajoie, I.; Bengio, Y.; Manzagol, P.-A. Stacked Denoising Autoencoders: Learning Useful Representations in a Deep Network with a Local Denoising Criterion. J. Mach. Learn. Res. 2010, 11, 3371–3408. [Google Scholar]
- Lin, L.; Song, X. Using CNN to Classify Hyperspectral Data Based on Spatial-spectral Information. In Proceedings of the 12th International Conference on Intelligent Information Hiding and Multimedia Signal Processing, Kaohsiung, Taiwan, 21–23 November 2016; Volume 64, pp. 61–68. [Google Scholar]
- Ghamisi, P.; Chen, Y.; Zhu, X.X. A Self-Improving Convolution Neural Network for the Classification of Hyperspectral Data. IEEE Geosci. Remote Sens. Lett. 2016, 13, 1537–1541. [Google Scholar] [CrossRef]
- Roux, N.L.; Bengio, Y. Representational power of restricted boltzmann machines and deep belief networks. Neural Comput. 2008, 20, 1631–1649. [Google Scholar] [CrossRef] [PubMed]
- Jia, Y.; Shelhamer, E.; Donahue, J.; Karayev, S.; Long, J.; Girshick, R.; Guadarrama, S.; Darrell, T. Caffe: Convolutional Architecture for Fast Feature Embedding. In Proceedings of the ACM Conference on Multimedia, Orlando, FL, USA, 3–7 November 2014; pp. 67–678. [Google Scholar]
- Lee, S.; Crawford, M.M. Hierarchical clustering approach for unsupervised image classification of hyperspectral data. IEEE Int. Geosci. Remote Sens. Symp. Proc. Sci. Soc. Explor. Manag. Chang. Planet. IGARSS 2004, 2, 941–944. [Google Scholar]
- Hinton, G.; Deng, L.; Yu, D.; Dahl, G.E.; Mohamed, A.-r.; Jaitly, N.; Senior, A.; Vanhoucke, V.; Nguyen, P.; Sainath, T.N.; et al. Deep Neural Networks for Acoustic Modeling in Speech Recognition: The Shared Views of Four Research Groups. IEEE Sigal Process. Mag. 2012, 29, 82–97. [Google Scholar] [CrossRef]
- Hinton, G.E. A Practical Guide to Training Restricted Boltzmann Machines. Momentum 2012, 9, 599–619. [Google Scholar]
- Carreira-Perpignan, M.A. On contrastive divergence learning. Artif. Intel. Stat. 2005, 5, 33–40. [Google Scholar]
- Hinton, G.E.; Salakhutdinov, R. Replicated softmax: An undirected topic model. Adv. Neural Inf. Process. Syst. 2009, 180, 1607–1614. [Google Scholar]
- Sutskever, I.; Tieleman, T. On the Convergence Properties of Contrastive Divergence. J. Mach. Learn. Res. 2010, 29, 789–795. [Google Scholar]
- Pan, S.J.; Yang, Q. A Survey on Transfer Learning. IEEE Trans. Knowl. Data Eng. 2010, 22, 1345–1359. [Google Scholar] [CrossRef] [Green Version]
- Bengio, Y. Deep Learning of Representations for Unsupervised and Transfer Learning. J. Mach. Learn. Res.-Proc. Track 2012, 27, 17–36. [Google Scholar]
- Pratt, L.Y. Discriminability-Based Transfer between Neural Networks. Adv. Neural Inf. Process. Syst. 1993, 5, 204–211. [Google Scholar]
- Nguyen, H.V.; Ho, H.T.; Patel, V.M.; Chellappa, R. DASH-N: Joint Hierarchical Domain Adaptation and Feature Learning. IEEE Trans. Image Process. 2015, 24, 5479–5491. [Google Scholar] [CrossRef]
- Hinton, G.E.; Osindero, S.; The, Y.W. A Fast Learning Algorithm for Deep Belief Nets. Neural Comput. 2014, 18, 1527–1554. [Google Scholar] [CrossRef] [PubMed]
- Yosinski, J.; Clune, J.; Bengio, Y.; Lipson, H. How transferable are features in deep neural networks. Adv. Neural Inf. Process. Syst. 2014, 27, 3320–3328. [Google Scholar]
- Dell’Acqua, F.; Gamba, P.; Ferrari, A.; Palmason, J.A.; Benediktsson, J.A.; Arnason, K. Exploiting spectral and spatial information in hyperspectral urban data with high resolution. IEEE Geosci. Remote Sens. Lett. 2004, 1, 322–326. [Google Scholar] [CrossRef]
- Fauvel, M.; Benediktsson, J.A.; Chanussot, J.; Sveinsson, J.R. Spectral and Spatial Classification of Hyperspectral Data Using SVMs and Morphological Profiles. IEEE Trans. Geosci. Remote Sens. 2008, 46, 3804–3814. [Google Scholar] [CrossRef] [Green Version]

















| Method | The Number of Layers from the Source Domain Data to the Target Domain Data | |||||
|---|---|---|---|---|---|---|
| 0 | 1 | 2 | 3 | 4 | 5 | |
| TSF-DBN-LR | 0.891 | 0.9012 | 0.9283 | 0.9108 | 0.8831 | 0.8666 |
| Sample Size | DBN Transfer Model | ||
|---|---|---|---|
| DBN-0 | DBN-1 | DBN-2 | |
| 30 | 0.759 | 0.832 | 0.824 |
| 60 | 0.821 | 0.862 | 0.872 |
| 90 | 0.886 | 0.895 | 0.893 |
| 120 | 0.81 | 0.9012 | 0.9283 |
| Sample Proportion | Spectral Feature | Spatial Feature | Joint spe–spa |
|---|---|---|---|
| 10% | 0.8532 | 0.8743 | 0.8921 |
| 20% | 0.8823 | 0.8967 | 0.9108 |
| 30% | 0.9011 | 0.9101 | 0.9236 |
| 40% | 0.9243 | 0.9283 | 0.9421 |
| 50% | 0.9291 | 0.9323 | 0.9460 |
| Method | Target Domain Dataset Label Sample Size (A/C) | |||
|---|---|---|---|---|
| 30 | 60 | 90 | 120 | |
| SVM | 0.701 | 0.759 | 0.786 | 0.801 |
| NBM | 0.621 | 0.651 | 0.681 | 0.711 |
| KNN | 0.675 | 0.732 | 0.743 | 0.776 |
| PCA+SVM | 0.751 | 0.821 | 0.853 | 0.887 |
| PCA+NBM | 0.701 | 0.753 | 0.761 | 0.811 |
| PCA+KNN | 0.731 | 0.802 | 0.831 | 0.867 |
| DBN+SVM | 0.832 | 0.862 | 0.895 | 0.9012 |
| DBN+NBM | 0.762 | 0.843 | 0.825 | 0.847 |
| DBN+KNN | 0.783 | 0.832 | 0.879 | 0.889 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, K.; Wang, M.; Liu, Y.; Yu, N.; Lan, W. A Novel Method of Hyperspectral Data Classification Based on Transfer Learning and Deep Belief Network. Appl. Sci. 2019, 9, 1379. https://doi.org/10.3390/app9071379
Li K, Wang M, Liu Y, Yu N, Lan W. A Novel Method of Hyperspectral Data Classification Based on Transfer Learning and Deep Belief Network. Applied Sciences. 2019; 9(7):1379. https://doi.org/10.3390/app9071379
Chicago/Turabian StyleLi, Ke, Mingju Wang, Yixin Liu, Nan Yu, and Wei Lan. 2019. "A Novel Method of Hyperspectral Data Classification Based on Transfer Learning and Deep Belief Network" Applied Sciences 9, no. 7: 1379. https://doi.org/10.3390/app9071379
APA StyleLi, K., Wang, M., Liu, Y., Yu, N., & Lan, W. (2019). A Novel Method of Hyperspectral Data Classification Based on Transfer Learning and Deep Belief Network. Applied Sciences, 9(7), 1379. https://doi.org/10.3390/app9071379