1. Introduction
Renewables energies represent a potential alternative in the transition towards a low-carbon society, where photovoltaic sources play a key role; however, consumers are also investors and a project is implemented only if economic conditions are verified [
1].
Solar technologies are characterized depending on the way they capture, convert, and distribute sunlight such as photovoltaic (PV) systems and their corresponding requirements for an energy storage arrangement [
2,
3]. Consequently, these technologies feed power to the electric grid by using solar panels as generators [
4,
5,
6]. In addition, concentrating solar power plants (CSP) use mirrors to focus the energy from the sun to drive traditional steam turbines or engines to create electricity; solar heating and cooling (SHC) systems which collect the thermal energy from the sun use this heat to provide hot water, space heating, and cooling for residential, commercial, and industrial applications. These technologies displace the need to use electricity or natural gas [
7,
8,
9].
A photovoltaic system is composed of several components: the solar panel and the inverter for grid-connected systems and additionally energy storage for stand-alone systems. The fabrication of the solar panel involves diverse stages. The first step is to define the type of panel, where the most known is monocrystalline or polycrystalline and where the solar cells are manufactured using wafers made of silicon [
10]. Nowadays, the PV systems are widely used to generate electricity due its accessible cost [
5,
6,
11,
12]. Some studies aimed at reducing this cost even more, e.g., in Reference [
13], a design optimization model for the residential PV systems in South Korea was proposed, where the objective function to be minimized consisted of three costs, such as the monthly electric bill, the PV-related construction costs, and the PV-related maintenance cost.
The solar radiation (photons) is responsible for the photovoltaic effect; nonetheless, some weather factors have an effect on the amount of energy generated even with the optimum radiation. A cloudy day generates a shadow on the solar panel by the time it has to capture the photons so that the incidence of these particles will be less, achieving a minor electric power. It is well-known that clouds are water steam concentrated in the air; in other words, humidity and temperature work together, and such a relation is an example of how the meteorological variables impact the generation of electric power [
14,
15].
Solar energy, besides wind energy, is currently the most resourceful renewable source worldwide [
16,
17]. Its obtainment, unlike many others currently used, does not mean any harm to the environment, and its resources overcome, by far, everyone else [
12,
18,
19,
20]. Some countries such as Germany, Italy, Spain, United States of America, and China are ahead on solar energy research; meanwhile in Mexico, being a country rich in solar radiation, with a great territorial extension, and having some solar energy studies, solar energy still does not have the necessary research compared to countries leading solar technology [
4,
5,
6,
11,
12,
21].
Figure 1 depicts the behavior of the horizontal solar radiation on the world. Similarly, if Mexico is compared with Europe, it can be seen that the only country with a notorious radiation incidence is Spain, achieving a maximum value between 4.8 and 5.4 kWh/m
2 [
22]. Mexico exceeds Spain both in incidence territory and in radiation intensity, with an average between 5.6 and 6.2 kWh/m
2, as can be seen in
Figure 2, exceeding even China, which mostly contemplates values of 4.6 kWh/m
2.
Table 1 shows the data compilation from 2010 describing the global-horizontal solar radiation for some locations in Mexico. The total irradiation provided by solar energy in the year 2018 was summarized in Reference [
25]. Both reports agree that the Northwest of Mexico reached the maximum values, the states of Sonora, Baja California, Coahuila, and Chihuahua being the main producers/receivers.
Recently, diverse reports have studied the relations between some meteorological variables and the electric power generated in a photovoltaic system. In Reference [
26], an analysis of the climatic factors and solar data from the Andes site was performed; nonetheless, all the data gathered for the study was averaged every 10 min and the power measurements were estimated. In [
27], the effect of diverse meteorological variables (outdoor temperature, air pressure, humidity, wind speed, and solar radiation) on the generated energy are mentioned, although a representative model of the plant was not obtained and all the data was experimentally generated. In Reference [
28], a statistical method was applied to forecast the energy generated by a solar plant, though a database of 30 plants from different locations is necessary and although it does not have real power measurements from the site and the computational load is heavy. In Reference [
29], an artificial neural network (ANN) is used to obtain a model to forecast the photovoltaic energy; however, the solar radiation was the only meteorological variable analyzed.
Higher Education Institutions (HEI) currently play a major role in the generation of human capital and the associated impact on societal development; HEIs are ideal locations to focus the resources in terms of the deployment and experimentation of decarbonization technologies to demonstrate the best practice for a further replication within wider society [
30].
Careful planning is required to manage the future electricity demand of PV systems due to its increasing potential demand in Mexico [
31,
32]. Therefore, it is vital to understand the influence of meteorological variables on energy consumption in which a better understanding of it can contribute to a more useful strategy in meeting the energy efficiency goal for the country.
According to the above and considering References [
1,
13,
30], the aim of this work is to present a statistical analysis based on the gradient descent method that is easy to implement and has a low computational load to estimate the electric power generation from the meteorological data such as the solar radiation, outdoor temperature, wind speed, and daylight time collected from PV systems located in Mexico City and Sonora [
33]. This is important because most of the current photovoltaic system deployments do not monitor these factors or employ them in adaptation and prediction tasks [
34,
35,
36].
The proposed methodology achieves a satisfactory estimation of the PV power with a high determination coefficient and a fair error percentage value.
Table 1.
The solar radiation on select places in Mexico (data in kWh/m
2 per day) [
37].
Table 1.
The solar radiation on select places in Mexico (data in kWh/m
2 per day) [
37].
| State | City | Jan | Feb | Mar | Apr | May | Jun | Jul | Aug | Sep | Oct | Nov | Dec | Avg |
|---|
| Sonora | Hermosillo | 4.0 | 4.6 | 5.4 | 6.6 | 8.3 | 8.5 | 6.9 | 6.6 | 6.7 | 6.0 | 4.7 | 3.9 | 6.0 |
| Sonora | Guaymas | 4.5 | 5.7 | 6.5 | 7.2 | 7.3 | 6.8 | 5.9 | 5.8 | 6.3 | 5.9 | 5.0 | 5.6 | 5.9 |
| Chihuahua | Chihuahua | 4.1 | 4.9 | 6.0 | 7.4 | 8.2 | 8.1 | 6.8 | 6.2 | 5.7 | 5.2 | 4.6 | 3.8 | 5.9 |
| SLP | SLP | 4.3 | 5.3 | 5.8 | 6.4 | 6.3 | 6.1 | 6.4 | 6.0 | 5.5 | 4.7 | 4.2 | 3.7 | 5.4 |
| Zacatecas | Zacatecas | 4.9 | 5.7 | 6.6 | 7.5 | 7.8 | 6.2 | 6.2 | 5.9 | 5.4 | 4.8 | 4.8 | 4.1 | 5.8 |
| Guanajuato | Guanajuato | 4.4 | 5.1 | 6.1 | 6.3 | 6.6 | 6.0 | 6.0 | 5.9 | 5.8 | 5.2 | 4.8 | 4.6 | 5.6 |
| Aguascalientes | Aguascalientes | 4.5 | 5.2 | 5.9 | 6.6 | 7.2 | 6.3 | 6.1 | 5.9 | 5.7 | 5.1 | 4.8 | 4.0 | 5.6 |
| Oaxaca | Salina Cruz | 5.4 | 6.3 | 6.6 | 6.4 | 6.1 | 5.0 | 5.6 | 5.9 | 5.2 | 5.9 | 5.7 | 5.2 | 5.8 |
| Oaxaca | Oaxaca | 4.9 | 5.7 | 5.8 | 5.5 | 6.0 | 5.4 | 5.9 | 5.6 | 5.0 | 4.9 | 4.8 | 4.4 | 5.3 |
| Jalisco | Colotlán | 4.6 | 5.7 | 6.5 | 7.5 | 8.2 | 6.6 | 5.8 | 5.6 | 5.8 | 5.3 | 4.9 | 4.1 | 5.9 |
| Jalisco | Guadalajara | 4.6 | 5.5 | 6.3 | 7.4 | 7.7 | 5.9 | 5.3 | 5.3 | 5.2 | 4.9 | 4.8 | 4.0 | 5.6 |
| Durango | Durango | 4.4 | 5.4 | 6.5 | 7.0 | 7.5 | 6.8 | 6 | 5.6 | 5.7 | 5.1 | 4.8 | 3.9 | 5.7 |
| Baja California | La Paz | 4.4 | 5.5 | 6.0 | 6.6 | 6.5 | 6.6 | 6.3 | 6.2 | 5.9 | 5.8 | 4.9 | 4.2 | 5.7 |
| Baja California | San Javier | 4.2 | 4.6 | 5.3 | 6.2 | 6.5 | 7.1 | 6.4 | 6.3 | 6.4 | 5.1 | 4.7 | 3.7 | 5.5 |
| Baja California | Mexicali | 4.1 | 4.4 | 5.0 | 5.6 | 6.6 | 7.3 | 7.0 | 6.1 | 6.1 | 5.5 | 4.5 | 3.9 | 5.5 |
| Querétaro | Querétaro | 5.0 | 5.7 | 6.4 | 6.8 | 6.9 | 6.4 | 6.4 | 6.4 | 6.3 | 5.4 | 5.0 | 4.4 | 5.9 |
| Puebla | Puebla | 4.9 | 5.5 | 6.2 | 6.4 | 6.1 | 5.7 | 5.8 | 5.8 | 5.2 | 5.0 | 4.7 | 4.4 | 5.5 |
| Hidalgo | Pachuca | 4.6 | 5.1 | 5.6 | 6.8 | 6.0 | 5.7 | 5.9 | 5.8 | 5.3 | 4.9 | 4.6 | 4.2 | 5.4 |
4. Conclusions
A gradient descent method was used to calculate, through a characteristic equation, the relationship between several variables which can be easily computed using quantitative data.
The results showed that solar radiation and daylight time are relevant in estimating the electric power, with solar radiation being the one with the most influence over the photovoltaic power generation; nonetheless, temperature, wind speed, and daylight hour affect this process, with their inclusion being fundamental in the analysis to achieve a proper electric power estimation.
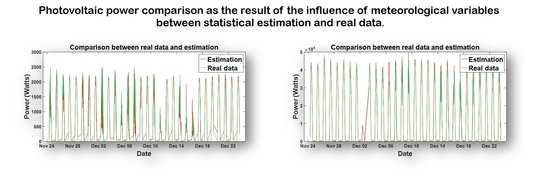
According to
Figure 9 and
Figure 16, an acceptable approximation between the statistical simulation results and real-time power generation has achieved. This is proven both by
Table 8, where 97.63% of the estimation results matches with the real data for HS and 99.66% match for MCS, and by
Table 9, achieving overall error values no greater than 7% and 2% for HS and MCS, respectively. An observable relationship between the determination coefficient values and error results is clear, concluding that the percentage error will be lower while
is higher.
Several causes could perturb the correlation, resulting in a wider dispersion, with the weather conditions as the most important for this study. Contrary to Mexico City, Hermosillo has abrupt changes in climate throughout the year, reaching temperatures around 50 °C and 0 °C in summer and winter, respectively, as well as sudden weather changes from a sunny day to a cloudy or even a rainy day within hours.
However, according to the above and even if the results have a satisfactory behavior, by definition, a statistical estimation will always have an error value. Nevertheless, these error values can be reduced, increasing the gathered input data or by other alternative methods such as intelligent systems which have proven to be an efficient methodology [
53,
54,
55,
56]. The above will be discussed elsewhere.