1. Introduction
On average, current inland cargo vessels generate lower external cargo transportation costs compared to other modes of freight transport, where the authors in [
1,
2,
3] define these costs as accidents, air pollution, climate, noise and congestion. Nevertheless, road-based cargo transport presently dominates the European hinterland freight transport [
4]. Therefore, the European Commission targets inducing a cargo transport modal shift from road to rail and waterborne transport [
5]. Subsequently, the European
[
6] project aims to facilitate this modal shift by constructing modular push vessels and barges which are either passive or self-propelled, in order to decouple sailing and transshipment time. The authors believe that an increase in the automation levels of these
vessels, and inland cargo vessels in general, could further help the envisaged cargo shift. Furthermore, they believe that this automation augmentation could potentially pave the way for future unmanned or autonomous inland cargo vessels.
Therefore, in [
7,
8], they constructed a scale model of such a European class type I [
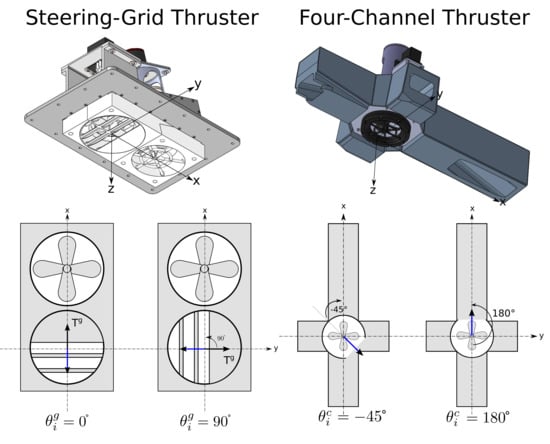
9] self-propelled inland cargo barge. These self-propelled barges navigate with a non-conventional, over-actuated, fully-embedded actuation system configuration consisting of a 360-degrees-steerable steering-grid thruster in the bow in conjunction with a 360-degrees-steerable four-channel thruster in the stern. Conventionally, inland vessels tend to have one or more propellers, regularly ducted to protect them and to increase their performance, which are often placed in conjunction with multiple rudders to boost their manoeuvrability. Occasionally, the addition of an azimuth or bow thruster further improves their manoeuvrability [
10,
11]. In comparison, conventional marine vessels have propeller(s)–rudder(s) configurations positioned at the stern [
12], and some marine vessels do carry more exotic propulsion systems such as transversal thrusters, azimuth thrusters, podded propellers, contra-rotating propellers, or even water jets for high speed vessels [
13]. In addition, be aware that most small unmanned surface vehicles (USVs) also make use of propeller–rudder configurations [
14]. However, some unmanned underwater vessels additionally utilise tunnel thrusters to increase their steering behaviour [
15].
Within this aforementioned accumulation of more conventional actuation systems, the tunnel and azimuth thrusters seem to show the largest similarities with the thrusters of this study. The general design and performance of the tunnel thrusters are discussed in [
16,
17]. Whereas the authors in [
18] review the different azimuth thruster designs, architectures, and working principles, the authors in [
19] additionally review complementary thruster phenomena such as thruster–thruster or thruster–hull interactions, and the author in [
20] published experimental data for an azimuth thruster during both static and dynamic operations. Unfortunately, the modelling literature for both systems is quite scarce. The existing research mostly uses the open-water propeller characteristics, as derived by [
21], for its starting point on which additional flow phenomena can be added. For example, the authors in [
22] built a mathematical manoeuvring model containing azimuth thrusters including thruster–thruster interactions. Similarly, the authors in [
15] suggested a tunnel thruster model for an underwater vehicle exhibiting small yaw or pitch angles, and noted the scarcity of available models, probably due to the complexity of the flow phenomena at hand. Albeit certain parallels can be drawn between the actuation system in this study and these more conventional tunnel and azimuth systems, the usability and adequacy of these conventional modelling approaches need to be investigated. Therefore, this study aims to:
- (i)
Detail the mechanical design of both the 360-degrees-steerable steering-grid thruster and the 360-degrees-steerable four-channel thruster nested inside the new fleet of barges.
- (ii)
Discuss, list, and show experimental towing tank data from both thrusters at different azimuth angles and propeller speeds, at zero advance speed.
- (iii)
Investigate the adequacy of the open-water propeller characteristics as the kernel of the theoretical thrust modelling approach.
- (iv)
Incorporate azimuth-angle-dependent internal and external hull thrust deduction losses by means of an extension to the theoretical model from (iii)
- (v)
Offer an additional artificial neural network modelling approach that might be useful to grip the current, and perhaps future, inherent complex flow phenomena occurring within both thrusters.
The successful completion of these aims offers the future researcher three different thrust characteristic descriptions (i.e., a data table (ii), an extended physically-based model (iii)+(iv), and an artificial neural network (v)) for both actuation systems (i). In addition to the insights that these data descriptions provide, their information can also be leveraged by advanced motion controllers, thrust allocation algorithms, and plant models. This paper continues as follows: first,
Section 2 shows the constructed vessel and details its non-conventional over-actuated propulsion system. Afterwards,
Section 3 expands the theoretical thrust model with angle-dependent thrust deductions and explains the multilayer neural network model structures. Subsequently,
Section 4 lists the experimental towing-tank data and feeds these data to both modelling methods. Finally,
Section 5 provides a comparison and discussion of the modelling results, and
Section 6 concludes this study.
5. Discussion
The pure experimental data of
Section 4.1 already expose interesting results for both thruster designs. On the one hand, they show the potential occurrence of a recirculation zone of flowing water for certain positions of the steering grid. On the other hand, they highlight the rather biased output angles of the resulting thrust forces of the four-channel thruster. Nevertheless, additional experiments (e.g., setups with different channel geometries and lengths, propeller diameters, steering-mechanism designs, etc.) could provide complementary insights in the complex flow phenomena arising in these thrusters. In addition, experiments with
could identify the wake factor which might depend on both the vessel velocity and the thruster location, i.e.,
. Similarly, these experiments could further investigate the adequacy of (
5) for these non-conventional thrusters. Note that the ambient flow, when
, does not decrease the thruster performance, but the complex interactions between the water outlet and the surrounding flow can decrease the effective thrust [
35]. Furthermore, experiments with dynamic propeller speeds could verify the adequacy of the existing dynamic thrust models, e.g., [
24]. Here, one should note that the ambient flow field tends to not have a large impact on the propulsion system dynamics [
36].
Given the complexity of the flow phenomena at hand, this study offered two model structure methodologies. Firstly,
Section 4.2 validated the theoretical propeller-characteristics thrust model structures of
Section 3.1 for both thruster designs by means of a bias-variance trade-off. This trade-off indicates that the quadratic propeller speed dependency indeed forms a simple but generic description of the resulting thrust forces for both embedded thruster designs at zero advance speed, although more complex model structures could be selected if desired by the end user. Moreover,
Section 4.2 further illustrated the successful modelling approach to capture the internal control-angle dependent thrust deductions that exist in both propulsion systems. Evidently, the aforementioned additional experimental setups could also help to further refine the propeller-characteristics based thrust model with the above-discussed possible extensions to this model. Secondly,
Section 4.3 demonstrated the possibility to use the multilayer feedforward networks from
Section 3.2 to grasp the complex water flows. Bearing in mind that these networks can serve as universal approximations of nonlinear functions, they offer the capability to model more complex flow phenomena that might occur during future experiments with dynamic propeller speeds or when
.
Figure 14 compares both model structure methodologies for the thrust forces generated by the four-channel thruster.
Figure 14a depicts the longitudinal modelled forces,
, whereas (b) shows the transversal modelled forces,
. For
, a quintic model describes
in conjunction with
for the propeller characteristics-based model, whereas a Bayesian regulated network of two hidden layers, with three neurons each, forms the neural network structure. A similar approach describes the structures of
, only here
has a quartic order. In both cases, i.e., (a) and (b), the neural networks seem to outperform the theoretically based models. Particularly in (b), the theoretical model generates a non-physical fit for
[−150°, −180°] whereas the neural network does not. In (a), for
[−60°, −120°] at
rpm, the theoretical model also offers an incorrect higher thrust force compared to the neural network which is closer to the data points. These differences could origin from the tendency of the higher order polynomials of
to over fit to the data set, whereas the
Ocam’s razor principle from the Bayesian regulation helps to avoid this situation.
Finally, the current and future identified model structures can provide inputs to several applications. For instance, they can illustrate the achieveable forces for a certain thruster over its whole control domain as exemplified by
Figure 15. Furthermore, these models can be used to augment certain links in the automation chain such as thrust allocation methods and motion controllers. For example, an optimal thrust allocation algorithm calculates the optimal thrust magnitudes and orientations for all onboard propulsion systems in order to achieve the desired force and moment output which the motion control calculated [
37]. Several implementations of these algorithms exist, such as a quadratic programming approach [
38,
39], or by using a linear pseudo-inverse model [
40]. However, these approaches tend to model the thrust forces as angle-independent, whereas the models of this study could be used to provide more accurate, control-angle dependent, representations of these forces. In addition, motion controllers could take the aforementioned and modelled constant thrust zones into account, similarly to incorporating dead-zones [
41,
42], further improving their performance. Furthermore, model predictive control architectures could also benefit from the suggested physically-based models as they can intrinsically integrate propulsion system limitations and states into their motion control design [
14,
43]. Moreover, these predictive controllers could also embed the developed neural networks [
44].