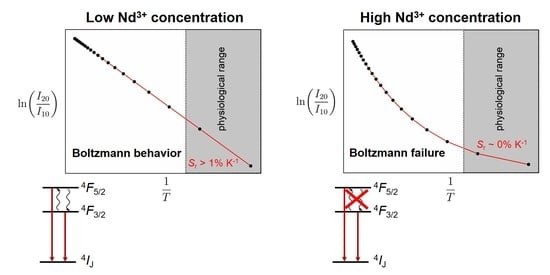
Making Nd3+ a Sensitive Luminescent Thermometer for Physiological Temperatures—An Account of Pitfalls in Boltzmann Thermometry
Abstract
:1. Introduction
2. Materials and Methods
2.1. Synthesis
2.2. Structural and Morphological Characterization
2.3. Diffuse Powder Reflectance Spectroscopy
2.4. (Time-Resolved) Luminescence Spectroscopy and Thermometry
3. Results and Discussion
3.1. Structural and Morphological Characterization of the Nd3+-Activated LaPO4 Nanocrystals
3.2. Diffuse Reflectance and Optical Absorption
3.3. Photoluminescence Properties and Luminescence Decay Dynamics—Predictions on Consequences for Thermometry with Nd3+
3.4. Consequences of Cross-Relaxation on Luminescence Thermometry Employing the 4F5/2 and 4F3/2 Spin-Orbit Levels of Nd3+
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Allison, S.W.; Gillies, G.T. Remote thermometry with thermographic phosphors: Instrumentation and applications. Rev. Sci. Instrum. 1997, 68, 2615–2650. [Google Scholar] [CrossRef]
- Cates, M.R.; Beshears, D.L.; Allison, S.W.; Simmons, C.M. Phosphor thermometry at cryogenic temperatures. Rev. Sci. Instrum. 1997, 68, 2412–2417. [Google Scholar] [CrossRef]
- Collins, S.F.; Baxter, G.W.; Wade, S.A.; Sun, T.; Grattan, K.T.V.; Zhang, Z.Y.; Palmer, A.W. Comparison of fluorescence-based temperature sensor schemes: Theoretical analysis and experimental validation. J. Appl. Phys. 1998, 84, 4649–4654. [Google Scholar] [CrossRef]
- Wade, S.A.; Collins, S.F.; Baxter, G.W. Fluorescence intensity ratio technique for optical fiber point temperature sensing. J. Appl. Phys. 2003, 94, 4743–4756. [Google Scholar] [CrossRef]
- Geitenbeek, R.G.; Nieuwelink, A.-E.; Jacobs, T.S.; Salzmann, B.B.V.; Goetze, J.; Meijerink, A.; Weckhuysen, B.M. In Situ Luminescence Thermometry to Locally Measure Temperature Gradients during Catalytic Reactions. ACS Catal. 2018, 8, 2397–2401. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Geitenbeek, R.G.; Vollenbroek, J.C.; Weijgertze, H.M.H.; Tregouet, C.B.M.; Nieuwelink, A.-E.; Kennedy, C.L.; Weckhuysen, B.M.; Lohse, D.; van Blaaderen, A.; van den Berg, A.; et al. Luminescence thermometry for in situ temperature measurements in microfluidic devices. Lab Chip 2019, 19, 1236–1246. [Google Scholar] [CrossRef] [Green Version]
- Ravenhorst, I.K.; Geitenbeek, R.G.; Eerden, M.J.; van Tijn Omme, J.; Peréz Garza, H.H.; Meirer, F.; Meijerink, A.; Weckhuysen, B.M. In Situ Local Temperature Mapping in Microscopy Nano-Reactors with Luminescence Thermometry. ChemCatChem 2019, 11, 5505–5512. [Google Scholar] [CrossRef] [Green Version]
- Jaque, D.; Vetrone, F. Luminescence nanothermometry. Nanoscale 2012, 4, 4301–4326. [Google Scholar] [CrossRef]
- Brites, C.D.S.; Lima, P.P.; Silva, N.J.O.; Millán, A.; Amaral, V.S.; Palacio, F.; Carlos, L.D. Thermometry at the nanoscale. Nanoscale 2012, 4, 4799–4829. [Google Scholar] [CrossRef] [Green Version]
- McLaurin, E.J.; Bradshaw, L.R.; Gamelin, D.R. Dual-Emitting Nanoscale Temperature Sensors. Chem. Mater. 2013, 25, 1283–1292. [Google Scholar] [CrossRef]
- Wang, X.-D.; Wolfbeis, O.S.; Meier, R.J. Luminescent probes and sensors for temperature. Chem. Soc. Rev. 2013, 42, 7834–7869. [Google Scholar] [CrossRef] [PubMed]
- Liu, T.-M.; Conde, J.; Lipiński, T.; Bednarkiewicz, A.; Huang, C.-C. Revisiting the classification of NIR-absorbing/emitting nanomaterials for in vivo bioapplications. NPG Asia Mater. 2016, 8, e295. [Google Scholar] [CrossRef]
- del Rosal, B.; Ximendes, E.; Rocha, U.; Jaque, D. In Vivo Luminescence Nanothermometry: From Materials to Applications. Adv. Opt. Mater. 2017, 5, 1600508. [Google Scholar] [CrossRef]
- Brites, C.D.S.; Balabhadra, S.; Carlos, L.D. Lanthanide-Based Thermometers: At the Cutting-Edge of Luminescence Thermometry. Adv. Opt. Mater. 2019, 7, 1801239. [Google Scholar] [CrossRef] [Green Version]
- Peng, H.; Stich, M.I.J.; Yu, J.; Sun, L.-N.; Fischer, L.H.; Wolfbeis, O.S. Luminescent Europium(III) nanoparticles for sensing and imaging of temperature in the physiological range. Adv. Mater. 2010, 22, 716–719. [Google Scholar] [CrossRef] [PubMed]
- Chambers, M.D.; Clarke, D.R. Doped Oxides for High-Temperature Luminescence and Lifetime Thermometry. Annu. Rev. Mater. Res. 2009, 39, 325–359. [Google Scholar] [CrossRef] [Green Version]
- Haro-González, P.; Martínez-Maestro, L.; Martín, I.R.; García-Solé, J.; Jaque, D. High-sensitivity fluorescence lifetime thermal sensing based on CdTe quantum dots. Small 2012, 8, 2652–2658. [Google Scholar] [CrossRef]
- Dramićanin, M.D. Sensing temperature via downshifting emissions of lanthanide-doped metal oxides and salts. A review. Methods Appl. Fluoresc. 2016, 4, 42001. [Google Scholar] [CrossRef] [Green Version]
- Peng, D.; Liu, Y.; Zhao, X.; Kim, K.C. Comparison of lifetime-based methods for 2D phosphor thermometry in high-temperature environment. Meas. Sci. Technol. 2016, 27, 95201. [Google Scholar] [CrossRef]
- Dramićanin, M.D.; Milićević, B.; Đorđević, V.; Ristić, Z.; Zhou, J.; Milivojević, D.; Papan, J.; Brik, M.G.; Ma, C.-G.; Srivastava, A.M.; et al. Li2TiO3:Mn4+ Deep-Red Phosphor for the Lifetime-Based Luminescence Thermometry. ChemistrySelect 2019, 4, 7067–7075. [Google Scholar] [CrossRef]
- Mendieta, A.; Fond, B.; Dragomirov, P.; Beyrau, F. A delayed gating approach for interference-free ratio-based phosphor thermometry. Meas. Sci. Technol. 2019, 30, 74002. [Google Scholar] [CrossRef]
- Souza, A.S.; Nunes, L.A.O.; Silva, I.G.N.; Oliveira, F.A.M.; da Luz, L.L.; Brito, H.F.; Felinto, M.C.F.C.; Ferreira, R.A.S.; Júnior, S.A.; Carlos, L.D.; et al. Highly-sensitive Eu3+ ratiometric thermometers based on excited state absorption with predictable calibration. Nanoscale 2016, 8, 5327–5333. [Google Scholar] [CrossRef] [PubMed]
- Marciniak, L.; Bednarkiewicz, A.; Elzbieciak, K. NIR–NIR photon avalanche based luminescent thermometry with Nd3+ doped nanoparticles. J. Mater. Chem. C 2018, 6, 7568–7575. [Google Scholar] [CrossRef]
- Trejgis, K.; Bednarkiewicz, A.; Marciniak, L. Engineering excited state absorption based nanothermometry for temperature sensing and imaging. Nanoscale 2020. [Google Scholar] [CrossRef] [PubMed]
- Rocha, J.; Brites, C.D.S.; Carlos, L.D. Lanthanide Organic Framework Luminescent Thermometers. Chem. Eur. J. 2016, 22, 14782–14795. [Google Scholar] [CrossRef] [PubMed]
- Kaczmarek, A.M.; Liu, Y.-Y.; Kaczmarek, M.K.; Liu, H.; Artizzu, F.; Carlos, L.D.; van der Voort, P. Developing Luminescent Ratiometric Thermometers Based on a Covalent Organic Framework (COF). Angew. Chem. 2020, 132, 1948–1956. [Google Scholar] [CrossRef] [Green Version]
- Smith, A.M.; Mancini, M.C.; Nie, S. Bioimaging: Second window for in vivo imaging. Nat. Nanotechnol. 2009, 4, 710–711. [Google Scholar] [CrossRef] [Green Version]
- Hemmer, E.; Venkatachalam, N.; Hyodo, H.; Hattori, A.; Ebina, Y.; Kishimoto, H.; Soga, K. Upconverting and NIR emitting rare earth based nanostructures for NIR-bioimaging. Nanoscale 2013, 5, 11339–11361. [Google Scholar] [CrossRef]
- Hemmer, E.; Benayas, A.; Légaré, F.; Vetrone, F. Exploiting the biological windows: Current perspectives on fluorescent bioprobes emitting above 1000 nm. Nanoscale Horiz. 2016, 1, 168–184. [Google Scholar] [CrossRef]
- Ximendes, E.C.; Santos, W.Q.; Rocha, U.; Kagola, U.K.; Sanz-Rodríguez, F.; Fernández, N.; Gouveia-Neto, A.d.S.; Bravo, D.; Domingo, A.M.; del Rosal, B.; et al. Unveiling in Vivo Subcutaneous Thermal Dynamics by Infrared Luminescent Nanothermometers. Nano Lett. 2016, 16, 1695–1703. [Google Scholar] [CrossRef]
- Ximendes, E.C.; Rocha, U.; del Rosal, B.; Vaquero, A.; Sanz-Rodríguez, F.; Monge, L.; Ren, F.; Vetrone, F.; Ma, D.; García-Solé, J.; et al. In Vivo Ischemia Detection by Luminescent Nanothermometers. Adv. Healthc. Mater. 2017, 6, 1601195. [Google Scholar] [CrossRef] [PubMed]
- Ximendes, E.C.; Rocha, U.; Sales, T.O.; Fernández, N.; Sanz-Rodríguez, F.; Martín, I.R.; Jacinto, C.; Jaque, D. In Vivo Subcutaneous Thermal Video Recording by Supersensitive Infrared Nanothermometers. Adv. Funct. Mater. 2017, 27, 1702249. [Google Scholar] [CrossRef]
- Santos, H.D.A.; Ximendes, E.C.; La Iglesias-de Cruz, M.d.C.; Chaves-Coira, I.; del Rosal, B.; Jacinto, C.; Monge, L.; Rubia-Rodríguez, I.; Ortega, D.; Mateos, S.; et al. In Vivo Early Tumor Detection and Diagnosis by Infrared Luminescence Transient Nanothermometry. Adv. Funct. Mater. 2018, 28, 1803924. [Google Scholar] [CrossRef]
- del Rosal, B.; Ruiz, D.; Chaves-Coira, I.; Juárez, B.H.; Monge, L.; Hong, G.; Fernández, N.; Jaque, D. In Vivo Contactless Brain Nanothermometry. Adv. Funct. Mater. 2018, 28, 1806088. [Google Scholar] [CrossRef] [Green Version]
- Laha, S.S.; Naik, A.R.; Kuhn, E.R.; Alvarez, M.; Sujkowski, A.; Wessells, R.J.; Jena, B.P. Nanothermometry Measure of Muscle Efficiency. Nano Lett. 2017, 17, 1262–1268. [Google Scholar] [CrossRef] [PubMed]
- Ortgies, D.H.; García-Villalón, Á.L.; Granado, M.; Amor, S.; Rodríguez, E.M.; Santos, H.D.A.; Yao, J.; Rubio-Retama, J.; Jaque, D. Infrared fluorescence imaging of infarcted hearts with Ag2S nanodots. Nano Res. 2019, 12, 749–757. [Google Scholar] [CrossRef]
- Shen, Y.; Lifante, J.; Ximendes, E.; Santos, H.D.A.; Ruiz, D.; Juárez, B.H.; Zabala Gutiérrez, I.; Torres Vera, V.; Rubio Retama, J.; Martín Rodríguez, E.; et al. Perspectives for Ag2S NIR-II nanoparticles in biomedicine: From imaging to multifunctionality. Nanoscale 2019, 11, 19251–19264. [Google Scholar] [CrossRef]
- Rocha, U.; Jacinto da Silva, C.; Ferreira Silva, W.; Guedes, I.; Benayas, A.; Martínez Maestro, L.; Acosta Elias, M.; Bovero, E.; van Veggel, F.C.J.M.; García Solé, J.A.; et al. Subtissue thermal sensing based on neodymium-doped LaF3 nanoparticles. ACS Nano 2013, 7, 1188–1199. [Google Scholar] [CrossRef]
- Marciniak, L.; Bednarkiewicz, A.; Kowalska, D.; Strek, W. A new generation of highly sensitive luminescent thermometers operating in the optical window of biological tissues. J. Mater. Chem. C 2016, 4, 5559–5563. [Google Scholar] [CrossRef]
- Rocha, U.; Jacinto, C.; Kumar, K.U.; López, F.J.; Bravo, D.; Solé, J.G.; Jaque, D. Real-time deep-tissue thermal sensing with sub-degree resolution by thermally improved Nd3+:LaF3 multifunctional nanoparticles. J. Lumin. 2016, 175, 149–157. [Google Scholar] [CrossRef]
- Vetrone, F.; Naccache, R.; Zamarrón, A.; La Juarranz de Fuente, A.; Sanz-Rodríguez, F.; Martinez Maestro, L.; Martín Rodriguez, E.; Jaque, D.; García Solé, J.; Capobianco, J.A. Temperature sensing using fluorescent nanothermometers. ACS Nano 2010, 4, 3254–3258. [Google Scholar] [CrossRef] [PubMed]
- Skripka, A.; Benayas, A.; Marin, R.; Canton, P.; Hemmer, E.; Vetrone, F. Double rare-earth nanothermometer in aqueous media: Opening the third optical transparency window to temperature sensing. Nanoscale 2017, 9, 3079–3085. [Google Scholar] [CrossRef] [Green Version]
- Mi, C.; Zhou, J.; Wang, F.; Lin, G.; Jin, D. Ultra-Sensitive Ratiometric Nanothermometer with Large Dynamic Range and Photostability. Chem. Mater. 2019. [Google Scholar] [CrossRef]
- Wawrzynczyk, D.; Bednarkiewicz, A.; Nyk, M.; Strek, W.; Samoc, M. Neodymium(III) doped fluoride nanoparticles as non-contact optical temperature sensors. Nanoscale 2012, 4, 6959–6961. [Google Scholar] [CrossRef]
- Marciniak, L.; Prorok, K.; Bednarkiewicz, A.; Kowalczyk, A.; Hreniak, D.; Strek, W. Water dispersible LiNdP4O12 nanocrystals: New multifunctional NIR–NIR luminescent materials for bio-applications. J. Lumin. 2016, 176, 144–148. [Google Scholar] [CrossRef]
- Boyer, J.-C.; Vetrone, F.; Cuccia, L.A.; Capobianco, J.A. Synthesis of colloidal upconverting NaYF4 nanocrystals doped with Er3+, Yb3+ and Tm3+, Yb3+ via thermal decomposition of lanthanide trifluoroacetate precursors. J. Am. Chem. Soc. 2006, 128, 7444–7445. [Google Scholar] [CrossRef]
- Boyer, J.-C.; Cuccia, L.A.; Capobianco, J.A. Synthesis of Colloidal Upconverting NaYF4:Er3+/Yb3+ and Tm3+/Yb3+ Monodisperse Nanocrystals. Nano Lett. 2007, 7, 847–852. [Google Scholar] [CrossRef]
- Wang, F.; Deng, R.; Liu, X. Preparation of core-shell NaGdF4 nanoparticles doped with luminescent lanthanide ions to be used as upconversion-based probes. Nat. Protoc. 2014, 9, 1634–1644. [Google Scholar] [CrossRef]
- Benayas, A.; del Rosal, B.; Pérez-Delgado, A.; Santacruz-Gómez, K.; Jaque, D.; Hirata, G.A.; Vetrone, F. Nd:YAG Near-Infrared Luminescent Nanothermometers. Adv. Opt. Mater. 2015, 3, 687–694. [Google Scholar] [CrossRef]
- Dantelle, G.; Matulionyte, M.; Testemale, D.; Cantarano, A.; Ibanez, A.; Vetrone, F. Nd3+ doped Gd3Sc2Al3O12 nanoparticles: Towards efficient nanoprobes for temperature sensing. Phys. Chem. Chem. Phys. 2019, 21, 11132–11141. [Google Scholar] [CrossRef]
- Skripka, A.; Morinvil, A.; Matulionyte, M.; Cheng, T.; Vetrone, F. Advancing neodymium single-band nanothermometry. Nanoscale 2019, 11, 11322–11330. [Google Scholar] [CrossRef] [PubMed]
- Dantelle, G.; Testemale, D.; Homeyer, E.; Cantarano, A.; Kodjikian, S.; Dujardin, C.; Hazemann, J.-L.; Ibanez, A. A new solvothermal method for the synthesis of size-controlled YAG:Ce single-nanocrystals. RSC Adv. 2018, 8, 26857–26870. [Google Scholar] [CrossRef] [Green Version]
- Suta, M.; Meijerink, A. A generalized theoretical framework of ratiometric single ion luminescent thermometers: Quantitative guidelines and limitations of the Boltzmann distribution for an optimum choice. 2020. to be submitted. [Google Scholar]
- Marciniak, Ł.; Bednarkiewicz, A.; Stefanski, M.; Tomala, R.; Hreniak, D.; Strek, W. Near infrared absorbing near infrared emitting highly-sensitive luminescent nanothermometer based on Nd3+ to Yb3+ energy transfer. Phys. Chem. Chem. Phys. 2015, 17, 24315–24321. [Google Scholar] [CrossRef] [PubMed]
- Marciniak, L.; Prorok, K.; Francés-Soriano, L.; Pérez-Prieto, J.; Bednarkiewicz, A. A broadening temperature sensitivity range with a core-shell YbEr@YbNd double ratiometric optical nanothermometer. Nanoscale 2016, 8, 5037–5042. [Google Scholar] [CrossRef] [PubMed]
- Haro-González, P.; Martín, I.R.; Martín, L.L.; León-Luis, S.F.; Pérez-Rodríguez, C.; Lavín, V. Characterization of Er3+ and Nd3+ doped Strontium Barium Niobate glass ceramic as temperature sensors. Opt. Mater. 2011, 33, 742–745. [Google Scholar] [CrossRef]
- Kolesnikov, I.E.; Kalinichev, A.A.; Kurochkin, M.A.; Mamonova, D.V.; Kolesnikov, E.Y.; Lähderanta, E.; Mikhailov, M.D. Bifunctional heater-thermometer Nd3+-doped nanoparticles with multiple temperature sensing parameters. Nanotechnology 2019, 30, 145501. [Google Scholar] [CrossRef]
- Geitenbeek, R.G.; de Wijn, H.W.; Meijerink, A. Non-Boltzmann Luminescence in NaYF4:Eu3+: Implications for Luminescence Thermometry. Phys. Rev. Appl. 2018, 10, 64006. [Google Scholar] [CrossRef] [Green Version]
- Silva, E.N.; Ayala, A.P.; Guedes, I.; Paschoal, C.W.A.; Moreira, R.L.; Loong, C.-K.; Boatner, L.A. Vibrational spectra of monazite-type rare-earth orthophosphates. Opt. Mater. 2006, 29, 224–230. [Google Scholar] [CrossRef]
- Ni, Y.; Hughes, J.M.; Mariano, A.N. Crystal chemistry of the monazite and xenotime structures. Am. Mineral. 1995, 80, 21–26. [Google Scholar] [CrossRef]
- Mullica, D.F.; Grossie, D.A.; Boatner, L.A. Structural refinements of praseodymium and neodymium orthophosphate. J. Solid State Chem. 1985, 58, 71–77. [Google Scholar] [CrossRef]
- Shannon, R.D. Revised Effective Ionic Radii and Systematic Studies of Interatomic Distances in Halides and Chalcogenides. Acta Cryst. A 1976, 32, 751–767. [Google Scholar] [CrossRef]
- Li, W.; Zhang, Q.; Joos, J.J.; Smet, P.F.; Schmedt auf der Günne, J. Blind spheres of paramagnetic dopants in solid state NMR. Phys. Chem. Chem. Phys. 2019, 21, 10185–10194. [Google Scholar] [CrossRef] [Green Version]
- Li, W.; Adlung, M.; Zhang, Q.; Wickleder, C.; Schmedt auf der Günne, J. A Guide to Brighter Phosphors-Linking Luminescence Properties to Doping Homogeneity Probed by NMR. ChemPhysChem 2019, 20, 3245–3250. [Google Scholar] [CrossRef] [Green Version]
- Li, W.; Smet, P.F.; Martin, L.I.D.J.; Pritzel, C.; Schmedt auf der Günne, J. Doping homogeneity in co-doped materials investigated at different length scales. Phys. Chem. Chem. Phys. 2020, 22, 818–825. [Google Scholar] [CrossRef] [Green Version]
- Marciniak, L.; Strek, W.; Guyot, Y.; Hreniak, D.; Boulon, G. Synthesis and Nd3+ Luminescence Properties of ALa1−xNdxP4O12 (A = Li, Na, K, Rb) Tetraphosphate Nanocrystals. J. Phys. Chem. C 2015, 119, 5160–5167. [Google Scholar] [CrossRef]
- Mayerhöfer, T.G.; Pipa, A.V.; Popp, J. Beer’s Law-Why Integrated Absorbance Depends Linearly on Concentration. ChemPhysChem 2019, 20, 2748–2753. [Google Scholar] [CrossRef]
- Görller-Walrand, C.; Binnemans, K. Spectral Intensities of f-f Transitions: Chapter 167. In Handbook on the Physics and Chemistry of Rare Earths; Gschneidner, K.A., Jr., Eyring, L., Eds.; Elsevier: Amsterdam, The Netherlands, 1998; pp. 101–264. [Google Scholar] [CrossRef]
- Ćirić, A.; Stojadinović, S.; Dramićanin, M.D. An extension of the Judd-Ofelt theory to the field of lanthanide thermometry. J. Lumin. 2019, 216, 116749. [Google Scholar] [CrossRef]
- Fong, F.K.; Diestler, D.J. Many-Body Processes in Nonradiative Energy Transfer between Ions in Crystals. J. Chem. Phys. 1972, 56, 2875–2880. [Google Scholar] [CrossRef]
- Carnall, W.T.; Goodman, G.L.; Rajnak, K.; Rana, R.S. A systematic analysis of the spectra of the lanthanides doped into single crystal LaF3. J. Chem. Phys. 1989, 90, 3443–3457. [Google Scholar] [CrossRef]











| La0.98Nd0.02PO4 | La0.95Nd0.05PO4 | La0.90Nd0.10PO4 | La0.75Nd0.25PO4 | NdPO4 | |
|---|---|---|---|---|---|
| /nm | 9.239(17) | 6.852(18) | 6.652(6) | 9.057(19) | 6.199(18) |
| a/Å | 6.8631(13) | 6.8504(14) | 6.8592(19) | 6.8390(15) | 6.8380(4) |
| b/Å | 7.1043(13) | 7.0901(13) | 7.0924(19) | 7.0799(15) | 6.9890(4) |
| c/Å | 6.5290(12) | 6.5171(12) | 6.5141(18) | 6.5053(14) | 6.4210(4) |
| V/Å3 | 309.84(21) | 308.08(39) | 308.44(23) | 306.57(26) | 298.67(11) |
| Strain % | 0.37(2) | 0.39(5) | 0.34(2) | 0.50(8) | 0.42(6) |
| Rp/% | 5.79 | 6.22 | 6.58 | 5.93 | 7.80 |
| Rwp/% | 4.36 | 4.61 | 4.85 | 4.47 | 5.78 |
| Rexp/% | 3.84 | 3.94 | 3.81 | 3.68 | 3.13 |
| G.o.f. | 1.50 | 1.58 | 1.72 | 1.61 | 2.49 |
| kr(4F3/2)/ms−1 | kr(4F5/2)/ms−1 | knr(0)/ms−1 | (298 K)/ms−1 | (298 K)/ms−1 |
|---|---|---|---|---|
| 2.25 | 3.16 ± 0.27 | 54.6 ± 4.7 | 219 ± 19 | 2.08 ± 0.18 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Suta, M.; Antić, Ž.; Ðorđević, V.; Kuzman, S.; Dramićanin, M.D.; Meijerink, A. Making Nd3+ a Sensitive Luminescent Thermometer for Physiological Temperatures—An Account of Pitfalls in Boltzmann Thermometry. Nanomaterials 2020, 10, 543. https://doi.org/10.3390/nano10030543
Suta M, Antić Ž, Ðorđević V, Kuzman S, Dramićanin MD, Meijerink A. Making Nd3+ a Sensitive Luminescent Thermometer for Physiological Temperatures—An Account of Pitfalls in Boltzmann Thermometry. Nanomaterials. 2020; 10(3):543. https://doi.org/10.3390/nano10030543
Chicago/Turabian StyleSuta, Markus, Željka Antić, Vesna Ðorđević, Sanja Kuzman, Miroslav D. Dramićanin, and Andries Meijerink. 2020. "Making Nd3+ a Sensitive Luminescent Thermometer for Physiological Temperatures—An Account of Pitfalls in Boltzmann Thermometry" Nanomaterials 10, no. 3: 543. https://doi.org/10.3390/nano10030543
APA StyleSuta, M., Antić, Ž., Ðorđević, V., Kuzman, S., Dramićanin, M. D., & Meijerink, A. (2020). Making Nd3+ a Sensitive Luminescent Thermometer for Physiological Temperatures—An Account of Pitfalls in Boltzmann Thermometry. Nanomaterials, 10(3), 543. https://doi.org/10.3390/nano10030543