Artificial Neural Network Modelling for Optimizing the Optical Parameters of Plasmonic Paired Nanostructures
Abstract
:1. Introduction
2. The Convergence of Machine Learning with Nanostructural Devices
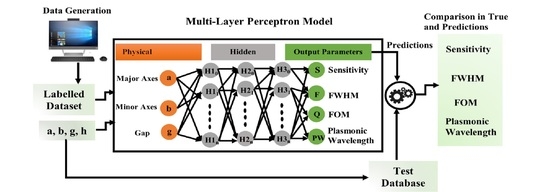
2.1. Artificial Neural Networks for Prediction of Output Parameters of Nanophotonic Structures
2.2. The Architecture of the Multilayer Artificial Neural Network
3. Neural Network Analysis with Empirical Evidences
3.1. Sensitivity (nm/RIU)
3.2. Plasmonic Wavelength
3.3. Full-Width Half Maximum (FWHM)
4. Comparison of Computational and Numerical Simulations Performance
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- McWilliams, A. The Maturing Nanotechnology Market: Products and Applications; BCC Research: Wellesley, MA, USA, 2016; pp. 8–20. [Google Scholar]
- Vance, M.E.; Kuiken, T.; Vejerano, E.P.; McGinnis, S.P.; Hochella, M.F., Jr.; Rejeski, D.; Hull, M.S. Nanotechnology in the real world: Redeveloping the nanomaterial consumer products inventory. Beilstein J. Nanotechnol. 2015, 6, 1769–1780. [Google Scholar] [CrossRef] [Green Version]
- LeCun, Y.; Bengio, Y.; Hinton, G. Deep learning. Nature 2015, 521, 436–444. [Google Scholar] [CrossRef]
- Massa, A.; Marcantonio, D.; Chen, X.; Li, M.; Salucci, M. DNNs as applied to electromagnetics, antennas, and propagation—A review. IEEE Antennas Wirel. Propag. Lett. 2019, 8, 2225–2229. [Google Scholar] [CrossRef]
- Chibani, S.; Coudert, F.X. Machine learning approaches for the prediction of materials properties. APL Mater. 2020, 8, 080701. [Google Scholar] [CrossRef]
- Zhou, J.; Huang, B.; Yan, Z.; Bünzli, J.C. Emerging role of machine learning in light-matter interaction. Light: Sci. Appl. 2019, 8, 1–7. [Google Scholar] [CrossRef] [Green Version]
- Jones, R.T. Machine Learning Methods in Coherent Optical Communication Systems. In International Series of Monographs on Physics; Technical University of Denmark: Kongens Lyngby, Denmark, 2019. [Google Scholar]
- Baxter, J.; Lesina, A.C.; Guay, J.M.; Ramunno, L. Machine Learning Applications in Plasmonics. In Proceedings of the 2018 Photonics North (PN), Montreal, QC, Canada, 5–7 June 2018. [Google Scholar]
- Kudyshev, Z.A.; Bogdanov, S.; Kildishev, A.V.; Boltasseva, A.; Shalaev, V.M. Machine learning assisted plasmonics and quantum optics. Metamater. Metadevices Metasyst. 2020, 11460, 1146018. [Google Scholar]
- Chen, H.; Bhuiya, A.M.; Liu, R.; Wasserman, D.M.; Toussaint, K.C., Jr. Design, fabrication, and characterization of near-IR gold bowtie nanoantenna arrays. J. Phys. Chem. C 2014, 118, 20553–20558. [Google Scholar] [CrossRef]
- Kakkava, E.; Rahmani, B.; Borhani, N.; Teğin, U.; Loterie, D.; Konstantinou, G.; Moser, C.; Psaltis, D. Imaging through multimode fibers using deep learning: The effects of intensity versus holographic recording of the speckle pattern. Opt. Fiber Technol. 2019, 52, 101985. [Google Scholar] [CrossRef]
- Schulz, K.; Hänsch, R.; Sörgel, U. Machine learning methods for remote sensing applications: An overview. In Earth Resources and Environmental Remote Sensing/GIS Applications IX (1079002); International Society for Optics and Photonics, SPIE Remote Sensing: Berlin, Germany, 2018. [Google Scholar]
- Horisaki, R. Optical Sensing and Control Based on Machine Learning. In Computational Optical Sensing and Imaging; Optical Society of America: Washington, DC, USA, 2018; p. CW3B-2. [Google Scholar]
- Amin, M.J.; Riza, N.A. Machine learning enhanced optical distance sensor. Opt. Commun. 2018, 407, 262–270. [Google Scholar] [CrossRef]
- Michelucci, U.; Baumgartner, M.; Venturini, F. Optical oxygen sensing with artificial intelligence. Sensors 2019, 19, 777. [Google Scholar] [CrossRef] [Green Version]
- Ma, L.; Liu, Y.; Zhang, X.; Ye, Y.; Yin, G.; Johnson, B.A. Deep learning in remote sensing applications: A meta-analysis and review. ISPRS J. Photogramm. Remote Sens. 2019, 152, 166–177. [Google Scholar] [CrossRef]
- Khan, Y.; Samad, A.; Iftikhar, U.; Kumar, S.; Ullah, N.; Sultan, J.; Ali, H.; Haider, M.L. Mathematical Modeling of Photonic Crystal based Optical Filters using Machine Learning. In Proceedings of the 2018 International Conference on Computing, Electronic and Electrical Engineering (ICE Cube), Quetta, Pakistan, 12–13 November 2018; pp. 1–5. [Google Scholar]
- Brown, K.A.; Brittman, S.; Maccaferri, N.; Jariwala, D.; Celano, U. Machine learning in nanoscience: Big data at small scales. Nano Lett. 2019, 20, 2–10. [Google Scholar] [CrossRef]
- Silva, G.A. A new frontier: The convergence of nanotechnology, brain machine interfaces, and artificial intelligence. Front. Neurosci. 2018, 12, 843. [Google Scholar] [CrossRef] [Green Version]
- Euler, H.C.; Boon, M.N.; Wildeboer, J.T.; Van de Ven, B.; Chen, T.; Broersma, H.; Bobbert, P.A.; Van der Wiel, W.G. A deep-learning approach to realizing functionality in nanoelectronic devices. Nat. Nanotechnol. 2020, 15, 992–998. [Google Scholar] [CrossRef]
- Bai, H.; Wu, S. Deep-learning-based nanowire detection in AFM images for automated nanomanipulation. Nanotechnol. Precis. Eng. 2021, 4, 013002. [Google Scholar] [CrossRef]
- Casañola-Martin, G.M. Machine Learning Applications in nanomedicine and nanotoxicology: An Overview. Int. J. Appl. Nanotechnol. Res. 2019, 4, 1–7. [Google Scholar] [CrossRef]
- Smajic, J.; Hafner, C.; Raguin, L.; Tavzarashvili, K.; Mishrikey, M. Comparison of numerical methods for the analysis of plasmonic structures. J. Comput. Theor. Nanosci. 2009, 6, 763–774. [Google Scholar] [CrossRef]
- Wiecha, P.R.; Muskens, O.L. Deep learning meets nanophotonics: A generalized accurate predictor for near fields and far fields of arbitrary 3D nanostructures. Nano Lett. 2019, 20, 329–338. [Google Scholar] [CrossRef] [Green Version]
- McKinney, W. Pandas, Python Data Analysis Library. 2021. Version: 1.3.2. Available online: http://pandas.pydata.org (accessed on 18 August 2021).
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V.; et al. Scikit-learn: Machine learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]
- McKinney, W. Python for Data Analysis: Data Wrangling with Pandas, NumPy, and IPython; O’Reilly Media, Inc.: North Sebastopol, CA, USA, 2012. [Google Scholar]
- Miller, H.; Haller, P.; Burmako, E.; Odersky, M. Instant pickles: Generating object-oriented pickler combinators for fast and extensible serialization. In Proceedings of the 2013 ACM SIGPLAN International Conference on Object Oriented Programming Systems Languages and Applications, Indianapolis, IN, USA, 29–31 October 2013; pp. 183–202. [Google Scholar]
- Lorica, B. Why AI and Machine Learning Researchers Are Beginning to Embrace Pytorch; O’Reilly Media Radar: Farnham, UK, 2017. [Google Scholar]
- Paszke, A.; Gross, S.; Chintala, S.; Chanan, G.; Yang, E.; DeVito, Z.; Lin, Z.; Desmaison, A.; Antiga, L.; Lerer, A. Automatic differentiation in Pytorch. In Proceedings of the 31st Conference on Neural Information Processing Systems (NIPS 2017), Long Beach, CA, USA, 4–9 December 2017. [Google Scholar]
- Yegulalp, S. Facebook Brings GPU-Powered Machine Learning to Python. InfoWorld. Available online: https://www.infoworld.com/article/3159120/facebook-brings-gpu-powered-machine-learning-to-python.html (accessed on 19 January 2017).
- Patel, M. When Two Trends Fuse: Pytorch and Recommender Systems; O’Reilly Media: Farnham, UK, 2018; Available online: https://www.oreilly.com/content/when-two-trends-fuse-pytorch-and-recommender-systems/ (accessed on 8 September 2019).
- Collobert, R.; Kavukcuoglu, K.; Farabet, C. Torch7: A Matlab-like Environment for Machine Learning. BigLearn NIPS Workshop. 2011. Available online: https://publications.idiap.ch/downloads/papers/2011/Collobert_NIPSWORKSHOP_2011.pdf (accessed on 18 July 2021).
- Johnson, P.B.; Christy, R.W. Optical constants of the noble metals. Phys. Rev. B 1972, 6, 4370. [Google Scholar] [CrossRef]
- Verma, S.; Ghosh, S.; Rahman, B.M. All-Opto Plasmonic-Controlled Bulk and Surface Sensitivity Analysis of a Paired Nano-Structured Antenna with a Label-Free Detection Approach. Sensors 2021, 21, 6166. [Google Scholar] [CrossRef]
- Chou Chao, C.T.; Chou Chau, Y.F.; Huang, H.J.; Kumara, N.T.; Kooh, M.R.; Lim, C.M.; Chiang, H.P. Highly sensitive and tunable plasmonic sensor based on a nanoring resonator with silver nanorods. Nanomaterials 2020, 10, 1399. [Google Scholar] [CrossRef]
- Amato, F.; López, A.; Peña-Méndez, E.M.; Vaňhara, P.; Hampl, A.; Havel, J. Artificial neural networks in medical diagnosis. J. Appl. Biomed. 2013, 11, 47–58. [Google Scholar] [CrossRef]
- Khan, F.N.; Fan, Q.; Lu, C.; Lau, A.P. An optical communication’s perspective on machine learning and its applications. J. Light. Technol. 2019, 37, 493–516. [Google Scholar] [CrossRef]
- Kingmam, D.P.; Ba, J. Adam: A method for stochastic optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar]
- Chau, Y.F.; Chao, C.T.; Huang, H.J.; Anwar, U.; Lim, C.M.; Voo, N.Y.; Mahadi, A.H.; Kumara, N.T.; Chiang, H.P. Plasmonic perfect absorber based on metal nanorod arrays connected with veins. Results Phys. 2019, 15, 102567. [Google Scholar] [CrossRef]
- Seber, G.A.; Lee, A.J. Linear Regression Analysis; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2012. [Google Scholar]









| Major Axis (nm) | Minor Axis (nm) | Gap(nm) | Sensitivity (nm/RIU) | FWHM (nm) | Plasmonic Wavelength (nm) | |
|---|---|---|---|---|---|---|
| count | 530 | 530 | 530 | 530 | 530 | 530 |
| mean | 89.69 | 49.54 | 39.5471 | 191.22 | 78.54 | 653.64 |
| Standard Deviation | 24.74 | 29.22 | 22.35 | 109.43 | 37.16 | 86.97 |
| Minima | 30.00 | 10.00 | 10.00 | 26.52 | 2.90 | 557.35 |
| Maxima | 130.00 | 130.00 | 80.00 | 595.04 | 202.40 | 1068.24 |
| Input Parameters | Simulated Data from COMSOL Multiphysics | Predicted Data from Artificial Neural Network | Abs Error | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Major Axes (nm) | Minor Axes (nm) | Gap (nm) | Sensitivity (nm/RIU) | FWHM (nm) | FOM | Plasmonic Wavelength (nm) | Sensitivity (nm/RIU) | FWHM (nm) | FOM | Plasmonic Wavelength (nm) | Sensitivity (nm/RIU) % |
| 60 | 20 | 40 | 147.2138 | 47.5796 | 12.9362 | 615.5012 | 146.9226 | 48.2208 | 12.7551 | 614.5826 | 0.19 |
| 80 | 30 | 80 | 163.8554 | 70.5513 | 8.8533 | 624.6127 | 163.6056 | 73.3072 | 8.5141 | 624.1441 | 0.15 |
| 85 | 45 | 25 | 171.4485 | 40.5550 | 17.8535 | 724.0533 | 170.1578 | 45.2992 | 16.0795 | 728.3898 | 0.75 |
| 90 | 50 | 90 | 135.1549 | 72.3698 | 8.4007 | 607.9604 | 135.6321 | 76.1116 | 7.9741 | 606.9173 | 0.35 |
| 100 | 40 | 60 | 197.3106 | 67.2607 | 9.5097 | 639.6299 | 196.4355 | 66.1773 | 9.6454 | 638.3086 | 0.44 |
| 100 | 40 | 50 | 208.2831 | 69.2660 | 9.2666 | 641.8674 | 208.2168 | 70.5940 | 9.0697 | 640.2649 | 0.03 |
| 100 | 50 | 90 | 170.0086 | 79.0452 | 7.8709 | 622.1600 | 171.1509 | 82.6979 | 7.5360 | 623.2143 | 0.67 |
| 110 | 50 | 110 | 193.4595 | 90.4005 | 7.1131 | 643.0292 | 194.6961 | 92.8461 | 6.9959 | 649.5304 | 0.64 |
| 115 | 25 | 25 | 307.8743 | 100.8810 | 7.7953 | 786.4027 | 307.7973 | 100.0813 | 7.8181 | 782.4466 | 0.02 |
| 120 | 60 | 90 | 202.0654 | 125.9891 | 5.1380 | 647.3321 | 202.4991 | 118.7540 | 5.4480 | 646.9770 | 0.21 |
| 120 | 50 | 110 | 231.9397 | 105.6556 | 6.3215 | 667.9105 | 224.0618 | 105.1861 | 6.3483 | 667.7588 | 3.39 |
| 120 | 60 | 120 | 208.3476 | 105.9363 | 6.1832 | 655.0344 | 208.6262 | 104.3657 | 6.2874 | 656.1949 | 0.13 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Verma, S.; Chugh, S.; Ghosh, S.; Rahman, B.M.A. Artificial Neural Network Modelling for Optimizing the Optical Parameters of Plasmonic Paired Nanostructures. Nanomaterials 2022, 12, 170. https://doi.org/10.3390/nano12010170
Verma S, Chugh S, Ghosh S, Rahman BMA. Artificial Neural Network Modelling for Optimizing the Optical Parameters of Plasmonic Paired Nanostructures. Nanomaterials. 2022; 12(1):170. https://doi.org/10.3390/nano12010170
Chicago/Turabian StyleVerma, Sneha, Sunny Chugh, Souvik Ghosh, and B. M. Azizur Rahman. 2022. "Artificial Neural Network Modelling for Optimizing the Optical Parameters of Plasmonic Paired Nanostructures" Nanomaterials 12, no. 1: 170. https://doi.org/10.3390/nano12010170
APA StyleVerma, S., Chugh, S., Ghosh, S., & Rahman, B. M. A. (2022). Artificial Neural Network Modelling for Optimizing the Optical Parameters of Plasmonic Paired Nanostructures. Nanomaterials, 12(1), 170. https://doi.org/10.3390/nano12010170