Cluster Formation Effect of Water on Pristine and Defective MoS2 Monolayers
Abstract
:1. Introduction
2. Computational Details
3. Results
3.1. Configurations of (H2O)n on MoS2 Monolayers
3.2. Electronic Properties
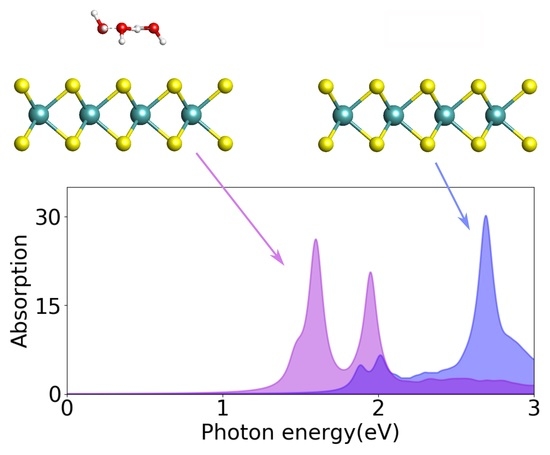
3.3. Optical and Excitonic Properties
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Gusakova, J.; Wang, X.; Shiau, L.L.; Krivosheeva, A.; Shaposhnikov, V.; Borisenko, V.; Gusakov, V.; Tay, B.K. Electronic Properties of Bulk and Monolayer TMDs: Theoretical Study Within DFT Framework (GVJ-2e Method). Phys. Status Solidi A 2017, 214, 1700218. [Google Scholar] [CrossRef]
- Kylänpää, I.; Komsa, H.-P. Binding energies of exciton complexes in transition metal dichalcogenide monolayers and effect of dielectric environment. Phys. Rev. B 2015, 92, 205418. [Google Scholar] [CrossRef] [Green Version]
- Berghäuser, G.; Malic, E. Analytical approach to excitonic properties of MoS2. Phys. Rev. B 2014, 89, 125309. [Google Scholar] [CrossRef] [Green Version]
- Ramasubramaniam, A. Large excitonic effects in monolayers of molybdenum and tungsten dichalcogenides. Phys. Rev. B 2012, 86, 115409. [Google Scholar] [CrossRef] [Green Version]
- He, K.; Kumar, N.; Zhao, L.; Wang, Z.; Mak, K.F.; Zhao, H.; Shan, J. Tightly Bound Excitons in Monolayer WSe2. Phys. Rev. Lett. 2014, 113, 026803. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Mak, K.F.; Lee, C.; Hone, J.; Shan, J.; Heinz, T.F. Atomically Thin MoS2: A New Direct-Gap Semiconductor. Phys. Rev. Lett. 2010, 105, 136805. [Google Scholar] [CrossRef] [Green Version]
- Mak, K.F.; He, K.; Shan, J.; Heinz, T.F. Control of valley polarization in monolayer MoS2 by optical helicity. Nat. Nanotechnol. 2012, 7, 494–498. [Google Scholar] [CrossRef] [PubMed]
- Splendiani, A.; Sun, L.; Zhang, Y.; Li, T.; Kim, J.; Chim, C.-Y.; Galli, G.; Wang, F. Emerging Photoluminescence in Monolayer MoS2. Nano Lett. 2010, 10, 1271–1275. [Google Scholar] [CrossRef]
- Hong, J.; Hu, Z.; Probert, M.; Li, K.; Lv, D.; Yang, X.; Gu, L.; Mao, N.; Feng, Q.; Xie, L.; et al. Exploring atomic defects in molybdenum disulphide monolayers. Nat. Commun. 2015, 6, 6293. [Google Scholar] [CrossRef] [Green Version]
- Zhou, W.; Zou, X.; Najmaei, S.; Liu, Z.; Shi, Y.; Kong, J.; Lou, J.; Ajayan, P.M.; Yakobson, B.I.; Idrobo, J.-C. Intrinsic structural defects in monolayer molybdenum disulfide. Nano Lett. 2013, 13, 2615–2622. [Google Scholar] [CrossRef]
- Stampfer, B.; Zhang, F.; Illarionov, Y.Y.; Knobloch, T.; Wu, P.; Waltl, M.; Grill, A.; Appenzeller, J.; Grasser, T. Characterization of Single Defects in Ultrascaled MoS2 Field-Effect Transistors. ACS Nano 2018, 12, 5368–5375. [Google Scholar] [CrossRef] [PubMed]
- Li, H.; Huang, M.; Cao, G. Markedly different adsorption behaviors of gas molecules on defective monolayer MoS2: A first-principles study. Phys. Chem. Chem. Phys. 2016, 18, 15110–15117. [Google Scholar] [CrossRef] [PubMed]
- González, C.; Biel, B.; Dappe, Y.J. Adsorption of small inorganic molecules on a defective MoS2 monolayer. Phys. Chem. Chem. Phys. 2017, 19, 9485–9499. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Li, F.; Shi, C. NO-sensing performance of vacancy defective monolayer MoS2 predicted by density function theory. Appl. Surf. Sci. 2017, 434, 294–306. [Google Scholar] [CrossRef]
- Lowe, B.M.; Maekawa, Y.; Shibuta, Y.; Sakata, T.; Skylaris, C.-K.; Green, N.G. Dynamic behaviour of the silica-water-bio electrical double layer in the presence of a divalent electrolyte. Phys. Chem. Chem. Phys. 2017, 19, 2687–2701. [Google Scholar] [CrossRef] [Green Version]
- Kokabu, T.; Inoue, S.; Matsumura, Y. Effect of molecular coverage on the electric conductance of a multi-walled carbon nanotube thin film. Chem. Phys. Lett. 2016, 654, 9–12. [Google Scholar] [CrossRef]
- Kokabu, T.; Takashima, K.; Inoue, S.; Matsumura, Y.; Yamamoto, T. Transport phenomena of electrons at the carbon nanotube interface with molecular adsorption. J. Appl. Phys. 2017, 122, 015308. [Google Scholar] [CrossRef]
- Melios, C.; Giusca, C.E.; Panchal, V.; Kazakova, O. Water on graphene: Review of recent progress. 2D Mater. 2018, 5, 022001. [Google Scholar] [CrossRef] [Green Version]
- Thiel, P.A.; Madey, T.E. The interaction of water with solid surfaces: Fundamental aspects. Surf. Sci. Rep. 1987, 7, 211–385. [Google Scholar] [CrossRef]
- Henderson, M.A. The interaction of water with solid surfaces: Fundamental aspects revisited. Surf. Sci. Rep. 2002, 46, 1–308. [Google Scholar] [CrossRef]
- Hodgson, A.; Haq, S. Water adsorption and the wetting of metal surfaces. Surf. Sci. Rep. 2009, 64, 381–451. [Google Scholar] [CrossRef]
- Carrasco, J.; Hodgson, A.; Michaelides, A. A molecular perspective of water at metal interfaces. Nat. Mater. 2012, 11, 667–674. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Mitsui, T.; Rose, M.K.; Fomin, E.; Ogletree, D.F.; Salmeron, M. Water Diffusion and Clustering on Pd(111). Science 2002, 297, 1850–1852. [Google Scholar] [CrossRef] [PubMed]
- Dong, A.; Yan, L.; Sun, L.; Yan, S.; Shan, X.; Guo, Y.; Meng, S.; Lu, X. Identifying Few Molecule Water Clusters with High Precision on Au(111) Surface. ACS Nano 2018, 12, 6452–6457. [Google Scholar] [CrossRef] [PubMed]
- Tatarkhanov, M.; Ogletree, D.F.; Rose, F.; Mitsui, T.; Fomin, E.; Maier, S.; Rose, M.; Cerdá, J.I.; Salmeron, M. Metal- and Hydrogen-Bonding Competition during Water Adsorption on Pd(111) and Ru(0001). J. Am. Chem. Soc. 2009, 131, 18425–18434. [Google Scholar] [CrossRef] [PubMed]
- Drüppel, M.; Deilmann, T.; Krüger, P.; Rohlfing, M. Diversity of trion states and substrate effects in the optical properties of an MoS2 monolayer. Nat. Commun. 2017, 8, 2117. [Google Scholar] [CrossRef] [Green Version]
- Yue, Q.; Shao, Z.; Chang, S.; Li, J. Adsorption of gas molecules on monolayer MoS2 and effect of applied electric field. Nanoscale Res. Lett. 2013, 8, 425. [Google Scholar] [CrossRef] [Green Version]
- Zhao, S.; Xue, J.; Kang, W. Gas adsorption on MoS2 monolayer from first-principles calculations. Chem. Phys. Lett. 2014, 595, 35–42. [Google Scholar] [CrossRef] [Green Version]
- Ferreira, F.; Carvalho, A.; Moura, Í.J.M.; Coutinho, J.; Ribeiro, R.M. Adsorption of H2, O2, H2O, OH and H on monolayer MoS2. J. Phys. Condens. Matter 2018, 30, 035003. [Google Scholar] [CrossRef] [Green Version]
- Levita, G.; Restuccia, P.; Righi, M.C. Graphene and MoS2 interacting with water: A comparison by ab initio calculations. Carbon 2016, 107, 878–884. [Google Scholar] [CrossRef]
- Hybertsen, M.S.; Louie, S.G. Electron correlation in semiconductors and insulators: Band gaps and quasiparticle energies. Phys. Rev. B 1986, 34, 5390–5413. [Google Scholar] [CrossRef] [PubMed]
- Rohlfing, M.; Louie, S.G. Electron-Hole Excitations in Semiconductors and Insulators. Phys. Rev. Lett. 1998, 81, 2312–2315. [Google Scholar] [CrossRef]
- Benedict, L.X.; Shirley, E.L.; Bohn, R.B. Optical Absorption of Insulators and the Electron-Hole Interaction: An Ab Initio Calculation. Phys. Rev. Lett. 1998, 80, 4514–4517. [Google Scholar] [CrossRef] [Green Version]
- Enkovaara, J.; Rostgaard, C.; Mortensen, J.J.; Chen, J.; Dułak, M.; Ferrighi, L.; Gavnholt, J.; Glinsvad, C.; Haikola, V.; Hansen, H.A.; et al. Electronic structure calculations with GPAW: A real-space implementation of the projector augmented-wave method. J. Phys. Condens. Matter 2010, 22, 253202. [Google Scholar] [CrossRef]
- Berland, K.; Hyldgaard, P. Exchange functional that tests the robustness of the plasmon description of the van der Waals density functional. Phys. Rev. B 2014, 89, 035412. [Google Scholar] [CrossRef] [Green Version]
- Qiu, H.; Xu, T.; Wang, Z.; Ren, W.; Nan, H.; Ni, Z.; Chen, Q.; Yuan, S.; Miao, F.; Song, F.; et al. Hopping transport through defect-induced localized states in molybdenum disulphide. Nat. Commun. 2013, 4, 2642. [Google Scholar] [CrossRef] [Green Version]
- Wilson, J.A.; Yoffe, A.D. The transition metal dichalcogenides discussion and interpretation of the observed optical, electrical and structural properties. Adv. Phys. 1969, 18, 193–335. [Google Scholar] [CrossRef]
- Rasmussen, F.A.; Thygesen, K.S. Computational 2D Materials Database: Electronic Structure of Transition-Metal Dichalcogenides and Oxides. J. Phys. Chem. C 2015, 119, 13169–13183. [Google Scholar] [CrossRef]
- Wang, K.; Paulus, B. Tuning the binding energy of excitons in the MoS2 monolayer by molecular functionalization and defective engineering. Phys. Chem. Chem. Phys. 2020, 22, 11936–11942. [Google Scholar] [CrossRef]
- Tang, W.; Sanville, E.; Henkelman, G. A grid-based Bader analysis algorithm without lattice bias. J. Phys. Condens. Matter 2009, 21, 084204. [Google Scholar] [CrossRef]
- Kresse, G.; Hafner, J. Ab initio molecular dynamics for liquid metals. Phys. Rev. B 1993, 47, 558–561. [Google Scholar] [CrossRef] [PubMed]
- Kresse, G.; Furthmüller, J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 1996, 54, 11169–11186. [Google Scholar] [CrossRef] [PubMed]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Árnadóttir, L.; Stuve, E.M.; Jónsson, H. Adsorption of water monomer and clusters on platinum(111) terrace and related steps and kinks: I. Configurations, energies, and hydrogen bonding. Surf. Sci. 2010, 604, 1978–1986. [Google Scholar] [CrossRef]
- Ludwig, R. Water: From Clusters to the Bulk. Angew. Chem. Int. Ed. 2001, 40, 1808–1827. [Google Scholar] [CrossRef]
- Keutsch, F.N.; Saykally, R.J. Water clusters: Untangling the mysteries of the liquid, one molecule at a time. Proc. Natl. Acad. Sci. USA 2001, 98, 10533–10540. [Google Scholar] [CrossRef] [Green Version]
- Dunn, M.E.; Pokon, E.K.; Shields, G.C. The ability of the Gaussian-2, Gaussian-3, Complete Basis Set–QB3, and Complete Basis Set–APNO model chemistries to model the geometries of small water clusters. Int. J. Quantum Chem. 2004, 100, 1065–1070. [Google Scholar] [CrossRef] [Green Version]
- Shields, R.M.; Temelso, B.; Archer, K.A.; Morrell, T.E.; Shields, G.C. Accurate Predictions of Water Cluster Formation, (H2O)n=2−10. J. Phys. Chem. A 2010, 114, 11725–11737. [Google Scholar] [CrossRef] [Green Version]
- Klots, A.R.; Newaz, A.K.M.; Wang, B.; Prasai, D.; Krzyzanowska, H.; Lin, J.; Caudel, D.; Ghimire, N.J.; Yan, J.; Ivanov, B.L.; et al. Probing excitonic states in suspended two-dimensional semiconductors by photocurrent spectroscopy. Sci. Rep. 2014, 4, 6608. [Google Scholar] [CrossRef] [Green Version]
- Yu, H.; Cui, X.; Xu, X.; Yao, W. Valley excitons in two-dimensional semiconductors. Natl. Sci. Rev. 2015, 2, 57–70. [Google Scholar] [CrossRef]
- Mouri, S.; Miyauchi, Y.; Matsuda, K. Tunable Photoluminescence of Monolayer MoS2 via Chemical Doping. Nano Lett. 2013, 13, 5944–5948. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Tongay, S.; Zhou, J.; Ataca, C.; Liu, J.; Kang, J.S.; Matthews, T.S.; You, L.; Li, J.; Grossman, J.C.; Wu, J. Broad-Range Modulation of Light Emission in Two-Dimensional Semiconductors by Molecular Physisorption Gating. Nano Lett. 2013, 13, 2831–2836. [Google Scholar] [CrossRef] [PubMed]




| No. a | Ebind(eV) | Ead(eV) | h(Å) | ΔQ(e) b | Individual ΔQ(e) | ||||
|---|---|---|---|---|---|---|---|---|---|
| H2O(1) c | H2O(2) c | H2O(3) c | H2O(4) c | H2O(5) c | |||||
| 1a) | −0.140 | −0.140 | 2.976 | 0.006 | 0.006 | ||||
| 2a) | −0.488 | −0.273 | 2.866 | 0.017 | −0.005 | 0.022 | |||
| 3a) | −0.990 | −0.308 | 3.110 | 0.025 | 0.010 | 0.000 | 0.015 | ||
| 4a) | −1.649 | −0.402 | 3.193 | 0.022 | 0.008 | 0.001 | 0.012 | 0.001 | |
| 5a) | −2.127 | −0.486 | 3.177 | 0.020 | 0.011 | 0.002 | 0.007 | −0.003 | 0.003 |
| 1b) | −0.209 | −0.209 | 2.082 | 0.032 | 0.032 | ||||
| 2b) | −0.537 | −0.322 | 2.385 | 0.025 | 0.018 | 0.007 | |||
| 3b) | −1.029 | −0.347 | 2.849 | 0.032 | 0.023 | 0.004 | 0.005 | ||
| 4b) | −1.663 | −0.416 | 2.976 | 0.033 | 0.026 | 0.001 | 0.006 | 0.001 | |
| 5b) | −2.178 | −0.537 | 3.061 | 0.031 | 0.022 | 0.004 | −0.003 | 0.007 | 0.001 |
| No. | Eele(eV) | Eopt(eV) | Eext(eV) |
|---|---|---|---|
| pristine MoS2 | 2.48 | 1.89 | 0.59 |
| 1a) | 2.48 | 1.64 | 0.84 |
| 2a) | 2.48 | 1.49 | 0.99 |
| 3a) | 2.48 | 1.31 | 1.17 |
| 4a) | 2.48 | 1.3 | 1.18 |
| 5a) | 2.48 | 1.32 | 1.16 |
| defective MoS2 | 1.95 | 1.32 | 0.63 |
| 1b) | 1.95 | 1.17 | 0.78 |
| 2b) | 1.95 | 1.07 | 0.88 |
| 3b) | 1.95 | 0.88 | 1.07 |
| 4b) | 1.95 | 0.82 | 1.13 |
| 5b) | 1.95 | 0.86 | 1.09 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, K.; Paulus, B. Cluster Formation Effect of Water on Pristine and Defective MoS2 Monolayers. Nanomaterials 2023, 13, 229. https://doi.org/10.3390/nano13020229
Wang K, Paulus B. Cluster Formation Effect of Water on Pristine and Defective MoS2 Monolayers. Nanomaterials. 2023; 13(2):229. https://doi.org/10.3390/nano13020229
Chicago/Turabian StyleWang, Kangli, and Beate Paulus. 2023. "Cluster Formation Effect of Water on Pristine and Defective MoS2 Monolayers" Nanomaterials 13, no. 2: 229. https://doi.org/10.3390/nano13020229
APA StyleWang, K., & Paulus, B. (2023). Cluster Formation Effect of Water on Pristine and Defective MoS2 Monolayers. Nanomaterials, 13(2), 229. https://doi.org/10.3390/nano13020229