Multimode Graded Index Fiber with Random Array of Bragg Gratings and Its Raman Lasing Properties
Abstract
:1. Introduction
2. Materials and Methods
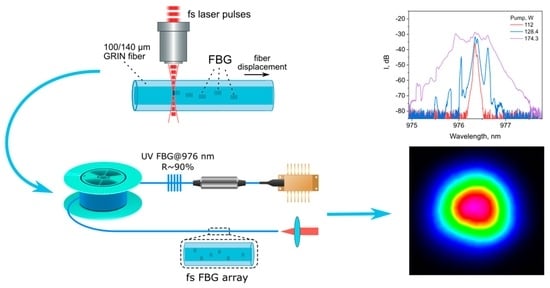
3. Results
4. Discussion and Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Richardson, D.J.; Fini, J.M.; Nelson, L.E. Space-division multiplexing in optical fibres. Nat. Photonics 2013, 7, 354–362. [Google Scholar] [CrossRef]
- Wright, L.G.; Christodoulides, D.N.; Wise, F.W. Controllable spatiotemporal nonlinear effects in multimode fibres. Nat. Photonics 2015, 9, 306–310. [Google Scholar] [CrossRef]
- Krupa, K.; Tonello, A.; Shalaby, B.M.; Fabert, M.; Barthélémy, A.; Millot, G.; Wabnitz, S.; Couderc, V. Spatial beam self-cleaning in multimode fibres. Nat. Photonics 2017, 11, 234–241. [Google Scholar] [CrossRef]
- Turitsyn, S.K.; Babin, S.A.; El-Taher, A.E.; Harper, P.; Churkin, D.V.; Kablukov, S.I.; Ania-Castañón, J.D.; Karalekas, V.; Podivilov, E.V. Random distributed feedback fibre laser. Nat. Photonics 2010, 4, 231–235. [Google Scholar] [CrossRef]
- Zhang, H.; Wu, J.; Wan, Y.; Wang, P.; Yang, B.; Xi, X.; Wang, X.; Zhu, P. Kilowatt random Raman fiber laser with full-open cavity. Opt. Lett. 2022, 47, 493–496. [Google Scholar] [CrossRef] [PubMed]
- Zhang, L.; Jiang, H.; Yang, X.; Pan, W.; Cui, S.; Feng, Y. Nearly-octave wavelength tuning of a continuous wave fiber laser. Sci. Rep. 2017, 7, 42611. [Google Scholar] [CrossRef]
- Babin, S.A.; Dontsova, E.I.; Kablukov, S.I. Random fiber laser directly pumped by a high-power laser diode. Opt. Lett. 2013, 38, 3301–3303. [Google Scholar] [CrossRef] [PubMed]
- Kablukov, S.I.; Dontsova, E.I.; Zlobina, E.A.; Nemov, I.N.; Vlasov, A.A.; Babin, S.A. An LD-pumped Raman fiber laser operating below 1 μm. Laser Phys. Lett. 2013, 10, 085103. [Google Scholar] [CrossRef]
- Yao, T.; Harish, A.; Sahu, J.; Nilsson, J. High-power continuous-wave directly-diode-pumped fiber Raman lasers. Appl. Sci. 2015, 5, 1323–1336. [Google Scholar] [CrossRef]
- Glick, Y.; Fromzel, V.; Zhang, J.; Ter-Gabrielyan, N.; Dubinskii, M. High efficiency, 154 W CW, diode pumped Raman fiber laser with brightness enhancement. Appl. Opt. 2017, 56, B97–B102. [Google Scholar] [CrossRef]
- Zlobina, E.A.; Kablukov, S.I.; Wolf, A.A.; Nemov, I.N.; Dostovalov, A.V.; Tyrtyshnyy, V.A.; Myasnikov, D.V.; Babin, S.A. Generating high-quality beam in a multimode LD-pumped all-fiber Raman laser. Opt. Express 2017, 25, 12581–12587. [Google Scholar] [CrossRef] [PubMed]
- Babin, S.A.; Zlobina, E.A.; Kablukov, S.I. Multimode Fiber Raman Lasers Directly Pumped by Laser Diodes. IEEE J. Sel. Top. Quantum Electron. 2018, 24, 1–10. [Google Scholar] [CrossRef]
- Supradeepa, V.R.; Feng, Y.; Nicholson, J.W. Raman fiber lasers. J. Opt. 2017, 19, 023001. [Google Scholar] [CrossRef]
- Terry, N.B.; Alley, T.G.; Russell, T.H. An explanation of SRS beam cleanup in graded-index fibers and the absence of SRS beam cleanup in step-index fibers. Opt. Express 2007, 15, 17509–17519. [Google Scholar] [CrossRef] [PubMed]
- Kuznetsov, A.G.; Kablukov, S.I.; Podivilov, E.V.; Babin, S.A. Brightness enhancement and beam profiles in an LD-pumped graded-index fiber Raman laser. OSA Contin. 2021, 4, 1034–1040. [Google Scholar] [CrossRef]
- Evmenova, E.A.; Kuznetsov, A.G.; Nemov, I.N.; Wolf, A.A.; Dostovalov, A.V.; Kablukov, S.I.; Babin, S.A. 2nd-order random lasing in a multimode diode-pumped graded-index fiber. Sci. Rep. 2018, 8, 17495. [Google Scholar] [CrossRef]
- Kuznetsov, A.G.; Nemov, I.N.; Wolf, A.A.; Evmenova, E.A.; Kablukov, S.I.; Babin, S.A. Cascaded Generation in Multimode Diode-Pumped Graded-Index Fiber Raman Lasers. Photonics 2021, 8, 447. [Google Scholar] [CrossRef]
- Chen, Y.; Fan, C.; Yao, T.; Xiao, H.; Leng, J.; Zhou, P.; Nemov, I.N.; Kuznetsov, A.G.; Babin, S.A. Brightness enhancement in random Raman fiber laser based on a graded-index fiber with high-power multimode pumping. Opt. Lett. 2021, 46, 1185–1188. [Google Scholar] [CrossRef]
- Kuznetsov, A.G.; Wolf, A.A.; Munkueva, Z.; Babin, S.A. Random lasing in multimode diode-pumped graded-index fiber based on artificial Rayleigh scattering in fs-inscribed random structure. Proc. SPIE 2022, 12310, 1231018. [Google Scholar]
- Gagné, M.; Kashyap, R. Demonstration of a 3 mW threshold Er-doped random fiber laser based on a unique fiber Bragg grating. Opt. Express 2009, 17, 19067–19074. [Google Scholar] [CrossRef]
- Lizárraga, N.; Puente, N.P.; Chaikina, E.I.; Leskova, T.A.; Mendez, E.R. Single-mode Er-doped fiber random laser with distributed Bragg grating feedback. Opt. Express 2009, 17, 395–404. [Google Scholar] [CrossRef] [PubMed]
- Gagné, M.; Kashyap, R. Random fiber Bragg grating Raman fiber laser. Opt. Lett. 2014, 39, 2755–2758. [Google Scholar] [CrossRef] [PubMed]
- Abdullina, S.R.; Skvortsov, M.I.; Vlasov, A.A.; Podivilov, E.V.; Babin, S.A. Coherent Raman lasing in a short polarization-maintaining fiber with a random fiber Bragg grating array. Laser Phys. Lett. 2019, 16, 105001. [Google Scholar] [CrossRef]
- Dostovalov, A.V.; Wolf, A.A.; Skvortsov, M.I.; Abdullina, S.R.; Kuznetsov, A.G.; Kablukov, S.I.; Babin, S.A. Femto-second-pulse inscribed FBGs for mode selection in multimode fiber lasers. Opt. Fiber Technol. 2019, 52, 101988. [Google Scholar] [CrossRef]
- Babin, S.A.; Kuznetsov, A.G.; Sidelnikov, O.S.; Wolf, A.A.; Nemov, I.N.; Kablukov, S.I.; Podivilov, E.V.; Fedoruk, M.P.; Wabnitz, S. Spatio-spectral beam control in multimode diode-pumped Raman fibre lasers via intracavity filtering and Kerr cleaning. Sci. Rep. 2021, 11, 21994. [Google Scholar] [CrossRef] [PubMed]
- Volyar, A.V.; Egorov, Y.A. Super pulses of orbital angular momentum in fractional-order spiroid vortex beams. Opt. Lett. 2018, 43, 74–77. [Google Scholar] [CrossRef]
- Kuznetsov, A.G.; Evmenova, E.A.; Dontsova, E.I.; Kablukov, S.I.; Babin, S.A. Frequency doubling of multimode diode-pumped GRIN-fiber Raman lasers. Opt. Express 2019, 27, 34760–34768. [Google Scholar] [CrossRef]






Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kuznetsov, A.G.; Wolf, A.A.; Munkueva, Z.E.; Dostovalov, A.V.; Babin, S.A. Multimode Graded Index Fiber with Random Array of Bragg Gratings and Its Raman Lasing Properties. Fibers 2023, 11, 48. https://doi.org/10.3390/fib11060048
Kuznetsov AG, Wolf AA, Munkueva ZE, Dostovalov AV, Babin SA. Multimode Graded Index Fiber with Random Array of Bragg Gratings and Its Raman Lasing Properties. Fibers. 2023; 11(6):48. https://doi.org/10.3390/fib11060048
Chicago/Turabian StyleKuznetsov, Alexey G., Alexey A. Wolf, Zhibzema E. Munkueva, Alexander V. Dostovalov, and Sergey A. Babin. 2023. "Multimode Graded Index Fiber with Random Array of Bragg Gratings and Its Raman Lasing Properties" Fibers 11, no. 6: 48. https://doi.org/10.3390/fib11060048
APA StyleKuznetsov, A. G., Wolf, A. A., Munkueva, Z. E., Dostovalov, A. V., & Babin, S. A. (2023). Multimode Graded Index Fiber with Random Array of Bragg Gratings and Its Raman Lasing Properties. Fibers, 11(6), 48. https://doi.org/10.3390/fib11060048